机器学习（六）——logistic回归

最新推荐文章于 2024-05-20 19:08:38 发布

又困又爱睡

最新推荐文章于 2024-05-20 19:08:38 发布

阅读量953

点赞数 24

分类专栏：机器学习文章标签：机器学习回归人工智能

本文链接：https://blog.csdn.net/qq_61179907/article/details/134600043

版权

机器学习专栏收录该内容

8 篇文章 0 订阅

订阅专栏

机器学习（六）——logistic回归

6.1 logistics回归概述
- 6.1.1 预备知识
6.2 实现
6.3 总结

6.1 logistics回归概述

logistic回归是一种二分类或多分类的概率型非线性回归模型，用于研究因变量与影响因素之间的关系。
其主要思想是根据现有数据对分类边界线建立回归公式，从而进行分类。与线性回归不同的是，logistics回归的目标是找到最佳拟合参数，以便对不同特征赋予不同的权重。

6.1.1 预备知识

6.1.1.1 线性模型与回归

线性模型的一般形式为：
$f ( x )= w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d} + b$
向量化表示为：
$f ( x )= w^{T} x + b$
其中x为d维属性描述样本为：
$x=(x_{1},x_{2},……,x_{d})$
目的：
学习一个线性模型以尽可能准确预测实值输出
即
$x_{i} + b\simeq y_{i}$

6.1.1.2 最小二乘法与参数求解

线性回归目标：回归预测值与真实值的误差最小。公式表示为：
$（w^{*} ，b^{*})=arg\min_{(w,b)} \sum_{i=1}^{m} (y_i-f(x_i))^2{} =arg\min_{(w,b)} \sum_{i=1}^{m} (y_i-wx_i-b)^2{}$
分别对w和b求偏导得到
$\frac {\partial E_ {(w,b)}}{\partial {w}} =2(w \sum _ {i=1}^ {m}x_ {i}^ {2} - \sum _ {i=1}^ {m}( y_ {i} -b) x_ {i} )=0$

$\frac {\partial E_ {(w,b)}}{\partial {b}} =2(mb- \sum _ {i=1}^ {m} ( y_ {i} - w_ {i} x_ {i} ))=0$

易得
$\frac {\sum _ {i=1}^ {m}y_ {i}(x_ {i}-\overline {x})}{\sum _ {i=1}^ {m}x_ {i}^ {2}-\frac {1}{m}(\sum _ {i=1}^ {m}x_ {i})^ {2}}$

$\frac {1}{m} \sum _ {i=1}^ {m} ( y_ {i} - wx_ {i} )$

$\bar{x} = \frac {1}{m} \sum _ {i=1}^ {m} x_{i}$

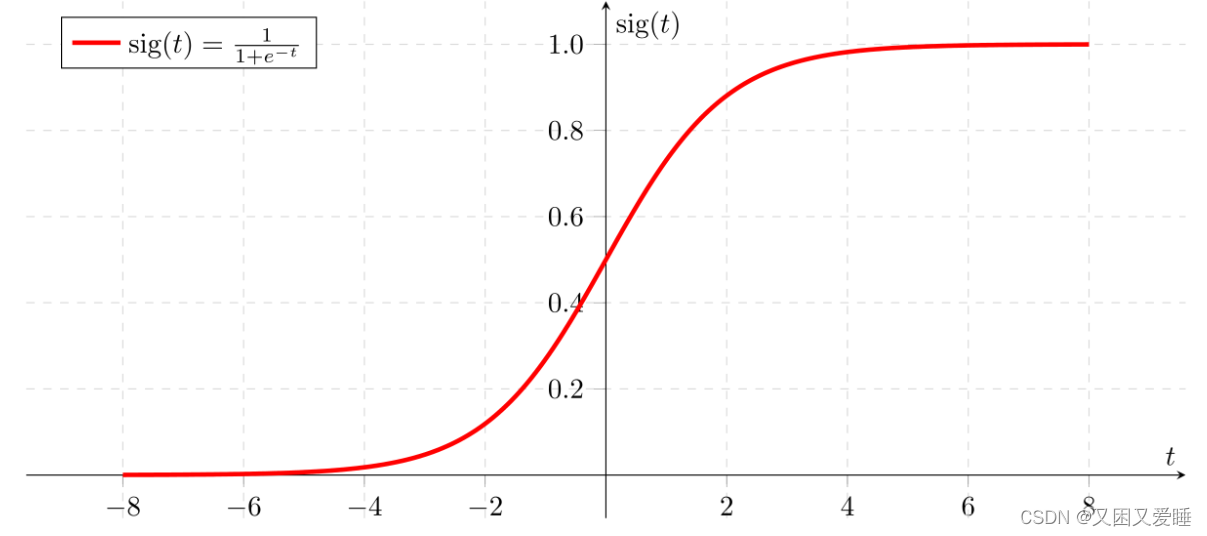
6.1.1.3 Sigmoid函数

Sigmoid函数是一种阶跃函数。在数学中,如果实数域上的某个函数可以用半开区间上的指示函数的有限次线性组合来表示，那么这个函数就是阶跃函数。而数学中指示函数是定义在某集合X上的函数，表示其中有哪些元素属于某一子集A。
为了实现Logistic回归分类器，我们在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代人Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类。所以，Logistic回归也可以被看成是一种概率估计。

函数如下：
$y=\frac{1}{1+e^{-z}} =\frac{1}{1+e^{-(w^Tx+b)}}$

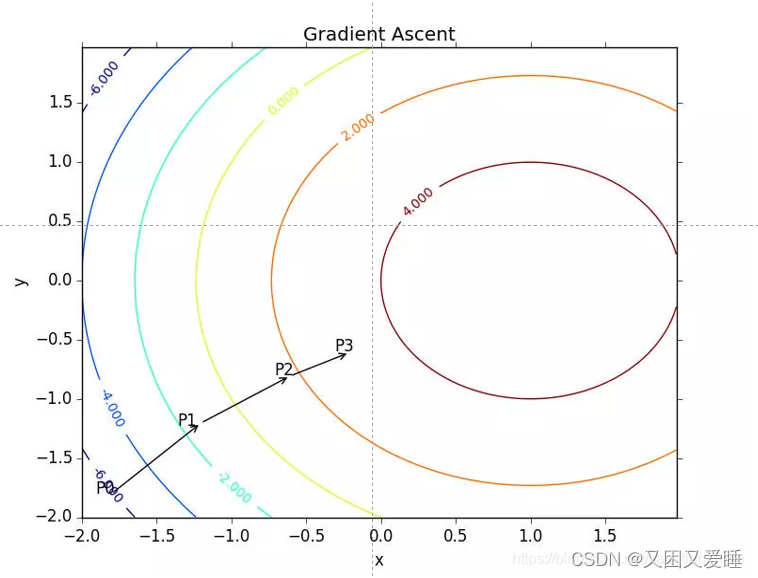
在这里插入图片描述

6.1.1.4 梯度上升法

要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。

梯度上升算法到达每个点后都会重新估计移动方向。从P0开始，计算完该点的梯度，函数就根据梯度移动到P2。如此循环直到满足停止条件。

在这里插入图片描述

6.2 实现

6.2.1 数据集介绍

源自《机器学习实战》数据集，形式为(x,y,label)

6.2.2 实现

loadDataSet ：用于读取训练数据集，将数据集分为特征矩阵（dataMat）和标签矩阵（labelMat）。

def loadDataSet(dataFileName):
    dataMat = []
    labelMat = []
    fr = open(dataFileName)
    for line in fr:
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))

    return dataMat, labelMat

sigmoid ：计算 sigmoid 函数的值，激活函数。

def sigmoid(x):
    return 1.0 / (1+math.exp(-x))

gradientAscent ：实现梯度上升法，优化权重向量（θ）。该函数接收数据矩阵、标签矩阵和学习率（alpha）作为输入参数。

def gradientAscent(dataMat, labelMat, alpha):
    m = len(dataMat)        #训练集个数
    n = len(dataMat[0])     #数据特征纬度
    theta = [0] * n

    iter = 1000
    while(iter):
        for i in range(m):
            hypothesis = sigmoid(computeDotProduct(dataMat[i], theta))
            error = labelMat[i] - hypothesis
            gradient = computeTimesVect(dataMat[i], error)
            theta = computeVectPlus(theta, computeTimesVect(gradient, alpha))
        iter -= 1
    return theta

newtonMethod ：实现牛顿法，优化权重向量（θ）。该函数接收数据矩阵、标签矩阵和迭代次数（iterNum）作为输入参数。

def newtonMethod(dataMat, labelMat, iterNum=10):
    m = len(dataMat)        #训练集个数
    n = len(dataMat[0])     #数据特征纬度
    theta = [0.0] * n

    while(iterNum):
        gradientSum = [0.0] * n
        hessianMatSum = [[0.0] * n]*n
        for i in range(m):
            try:
                hypothesis = sigmoid(computeDotProduct(dataMat[i], theta))
            except:
                continue
            error = labelMat[i] - hypothesis
            gradient = computeTimesVect(dataMat[i], error/m)
            gradientSum = computeVectPlus(gradientSum, gradient)
            hessian = computeHessianMatrix(dataMat[i], hypothesis/m)
            for j in range(n):
                hessianMatSum[j] = computeVectPlus(hessianMatSum[j], hessian[j])

        #计算hessian矩阵的逆矩阵有可能异常，如果捕获异常则忽略此轮迭代
        try:
            hessianMatInv = mat(hessianMatSum).I.tolist()
        except:
            continue
        for k in range(n):
            theta[k] -= computeDotProduct(hessianMatInv[k], gradientSum)

        iterNum -= 1
    return thet

computeHessianMatrix ：计算 Hessian 矩阵，用于牛顿法优化。

def computeHessianMatrix(data, hypothesis):
    hessianMatrix = []
    n = len(data)

    for i in range(n):
        row = []
        for j in range(n):
            row.append(-data[i]*data[j]*(1-hypothesis)*hypothesis)
        hessianMatrix.append(row)
    return hessianMatrix

computeDotProduct ：计算两个向量的点积。
computeVectPlus ：计算两个向量的和。
computeTimesVect ：计算某个向量的n倍。

def computeDotProduct(a, b):
    if len(a) != len(b):
        return False
    n = len(a)
    dotProduct = 0
    for i in range(n):
        dotProduct += a[i] * b[i]
    return dotProduct

def computeVectPlus(a, b):
    if len(a) != len(b):
        return False
    n = len(a)
    sum = []
    for i in range(n):
        sum.append(a[i]+b[i])
    return sum

def computeTimesVect(vect, n):
    nTimesVect = []
    for i in range(len(vect)):
        nTimesVect.append(n * vect[i])
    return nTimesVect

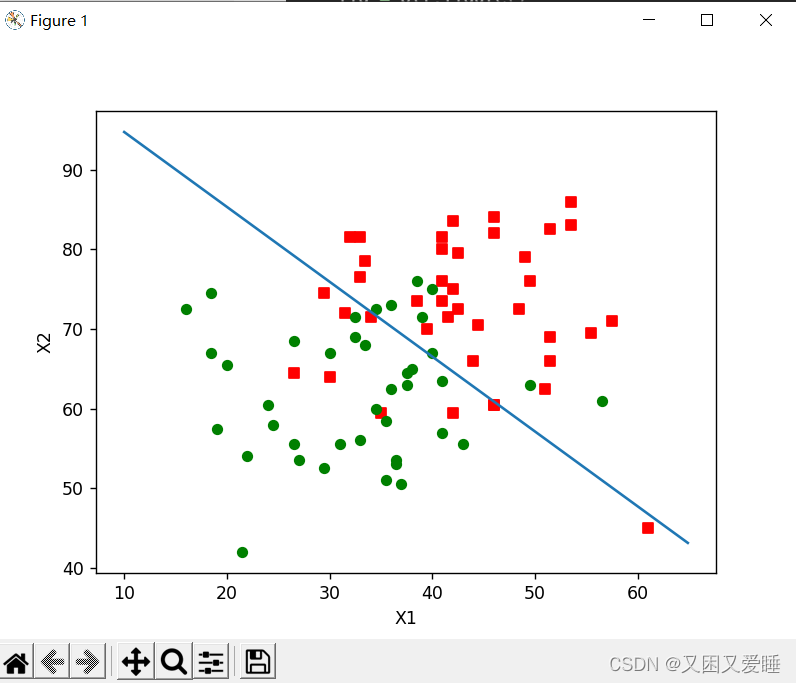
plotBestFit ：绘制最优拟合直线，展示分类结果。

def plotBestFit(dataMat, labelMat, weights):
    import matplotlib.pyplot as plt
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(10.0, 65.0, 0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()

classifyVector：对输入向量进行分类，判断其属于正类还是负类。

def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0
    else: return 0.0

6.2.3 结果

在这里插入图片描述

6.3 总结

6.3.1 优点

模型简单：Logistic回归的模型结构简单，易于理解和实现。
速度快：Logistic回归的计算速度相对较快，适合处理大量数据。
适应性：Logistic回归可以处理线性可分问题，对于某些场景具有较好的表现。
易于更新：Logistic回归模型可以容易地更新，吸收新的数据和特征。
稳定性：Logistic回归对异常值和不稳定数据具有一定的鲁棒性。减小极端情况的影响

6.3.2 缺点

适应性局限：Logistic回归是一个弱分类器，其对数据和场景的适应能力有限，不如决策树等算法强大。仅仅适应于线性分布
特征限制：Logistic回归在处理高维度特征时，表现不如其他算法，如支持向量机等。
无法处理非线性问题：Logistic回归本身仅适用于线性可分问题，处理非线性问题需要借助核技巧等方法。
参数敏感：Logistic回归的参数选择和调整较为复杂，容易受到数据影响，需要多次迭代和调参。
过拟合风险：Logistic回归有可能出现过拟合现象，需要采用特征选择、正则化等方法降低过拟合风险。

6.3.3 基于logistic的混沌加密

在伪混沌位序列产生方法上，采取不同μ值、不同初始状态值的两个不同 Logistic 混沌映射进行迭代,先让它们分别初始迭代m、n次（m≠n），再同时迭代，通过动态比较两个映射每次迭代的状态值，产生二进制伪混沌序列。具体算法是：

①在区间[3.57,4]中，选择两个不同的μ值，分别作为两个映射参数；

②在区间[0,1]中，选择两个不同的实数，分别作为两个映射迭代的初始状态值；

③在区间[50,100]中，选择两个不同的整数m和n，分别作为两个映射的初始迭代次数。两个映射先分别迭代m和n次，得到两个状态值xm和yn，然后再开始同时迭代，每次

迭代后，比较两个映射的状态值。如果两个映射分别表示为f1和f2，如果 f1(xm)> f2(yn)，产生二进制位‘1’；否则，产生二进制位‘0’。如此类推，形成伪混沌二进制位序列；

④读入明文信息，对每一个明文信息位，依据第③步算法，将两个映射迭代，比较每次迭代后的状态值，产生二进制位 0 或 1，并与明文信息位进行模 2 加运算，实现加密。该操作一直持续到将所有明文信息位加密完为止

6.3.4 softmax regression

Logistic Regression用来解决二分类问题，但若是遇到多分类问题我们常采取softmax regression，它是Logistic Regression在多分类问题上的推广。

又困又爱睡

关注

24
点赞
踩
20

收藏

觉得还不错? 一键收藏
0
评论
机器学习（六）——logistic回归

logistic回归是一种二分类或多分类的概率型非线性回归模型，用于研究因变量与影响因素之间的关系。其主要思想是根据现有数据对分类边界线建立回归公式，从而进行分类。与线性回归不同的是，logistics回归的目标是找到最佳拟合参数，以便对不同特征赋予不同的权重。源自《机器学习实战》数据集，形式为(x,y,label)模型简单：Logistic回归的模型结构简单，易于理解和实现。速度快：Logistic回归的计算速度相对较快，适合处理大量数据。
复制链接

扫一扫