练习放在文末
子群定义

注意H是非空子集
判定定理



定理2常用
生成子群

子群格

注意一下2元集
主要是具备最大上界,最小下届
循环群

这张图看一下就行了,不重要
定理1
例子

定理2
变换群
变换,置换,考试应该不考
例子

n元置换

上面这个感觉有点问题吧,可能是打错了——<b,d>

在第一个(1 2 3 4)中1后面跟着2,2后面跟着3,3后面跟着4,4后面回到1

奇、偶置换,交代群这个不重要
置换乘法(需要类比函数的合成)
如题
(18246573)
(1 2 3 4 5 6 7 8 9)
(8 4 1 6 7 5 3 2 9)
(132)(5648)
(1 2 3 4 5 6 7 8 9)
(3 1 2 8 6 4 7 5 9)
首先,逆序合成(如同函数合成)
接着,从第一个开始看:
第一个置换中1 下面对应 8
第二个置换中8 下面对应 5
(合成)乘法后的置换 1 下面对应 5
其他的以此类推
陪集

抽象地解释:
群G,子群H,根据H定义了一个G上的等价关系R,任意G中元素a,b,aRb if and only if ab^(-1)属于G,[a]=Ha,也会出现一个G的划分
性质

右陪集、左陪集
Lagrange定理
引理

定理及其推论
练习
16题
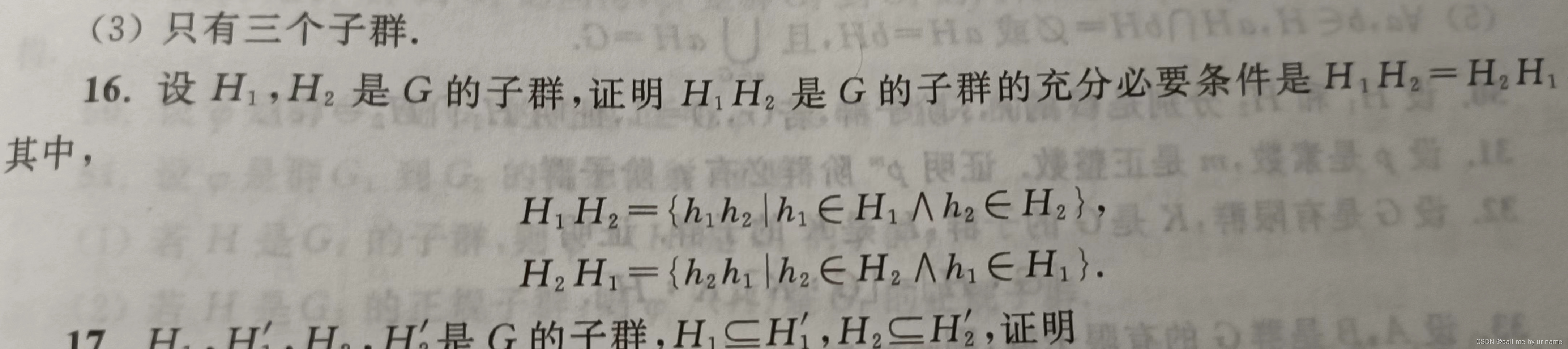


选择e来确定子代数非空,其他的,讲不出什么,主要还是认真看看,这题有点难
19题

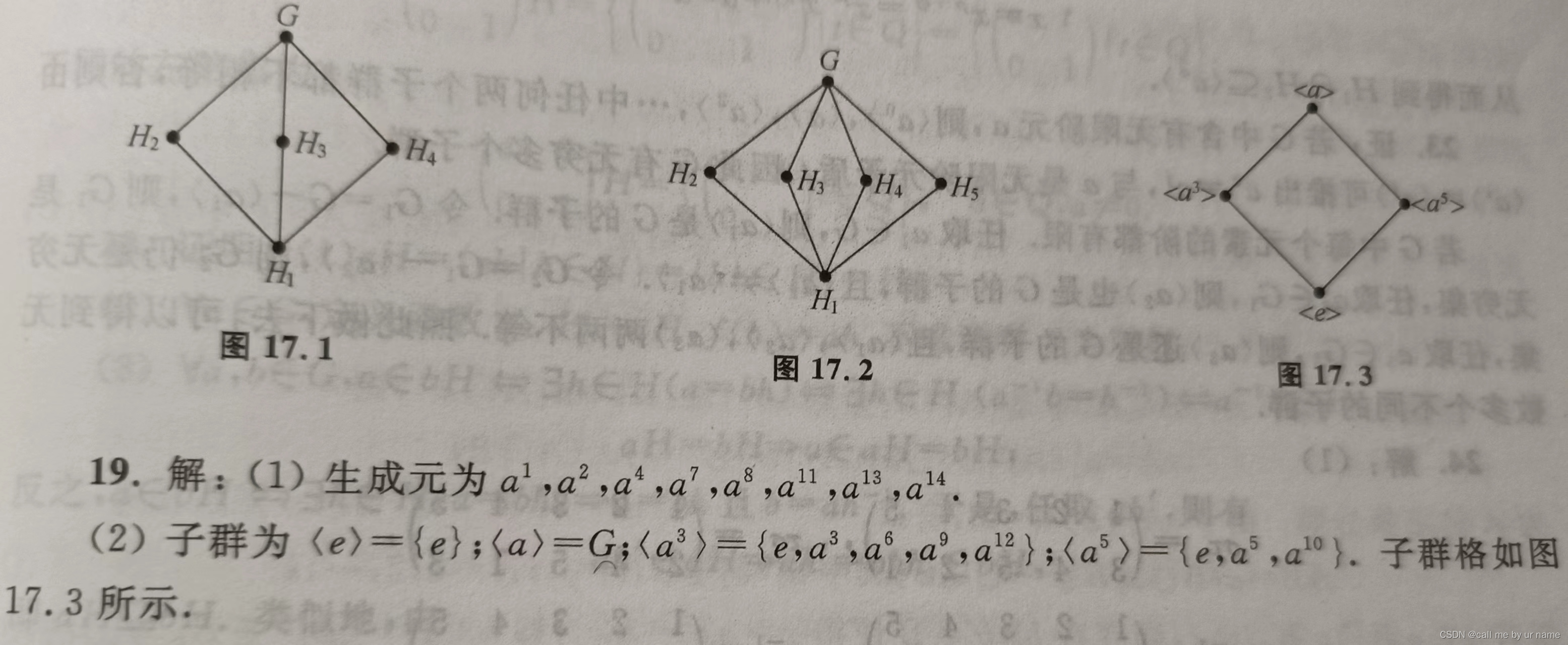
(1):
1.a^2自我循环8次,就变成了a^1,接着a^3……以此类推,所以a^2是生成元
2.a^3不是,因为a^3经过6次自我循环,又变成了a^3,所以不是
(其余的也是这个道理)
(2):
子群需要满足零元运算,所以不难循环出单位元的,不能算作子群
子群格要注意最上方一般是本身,最下方是单位元子群,注意中间的是否可以比较
之前写得不太对,这题翻上去看看循环群那里的知识就可以轻松解决
28题
32题

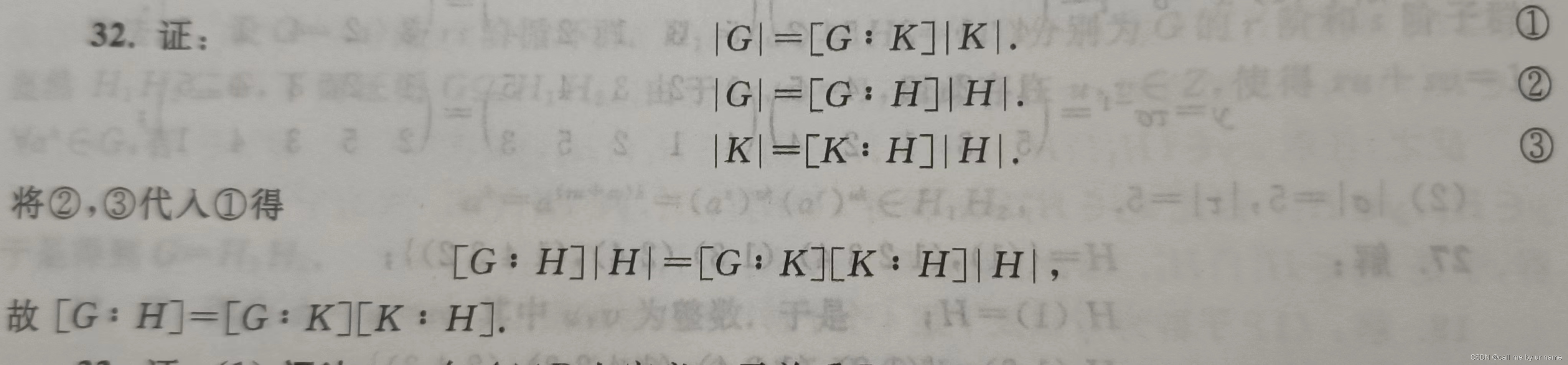
[G:H]——H在G中的指数,即H左(右)陪集数(左右陪集数是相等的) 【来源于lagrange定理】
这题主要是回忆并熟悉一下lagrange定理的知识,题目本身不难
47题

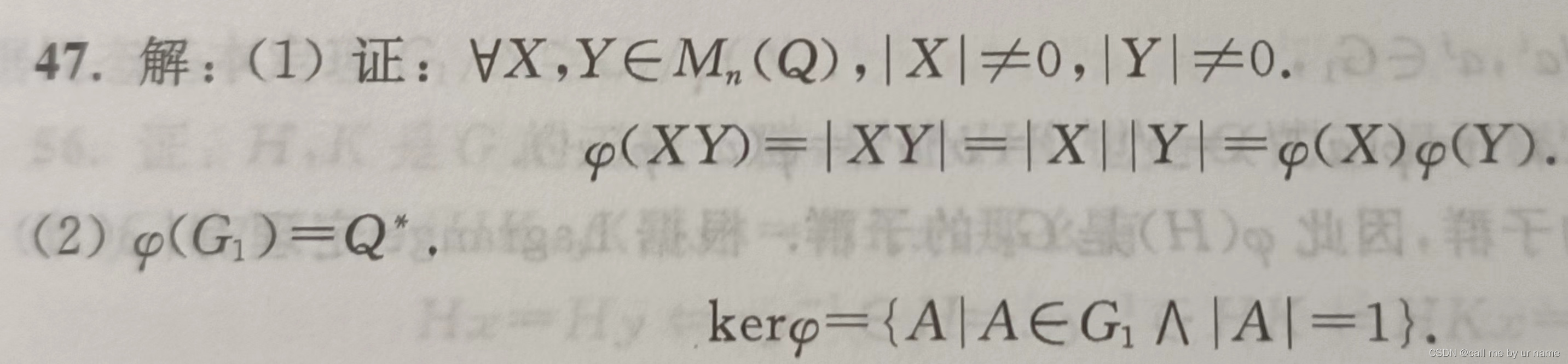
这题比较简单
49题

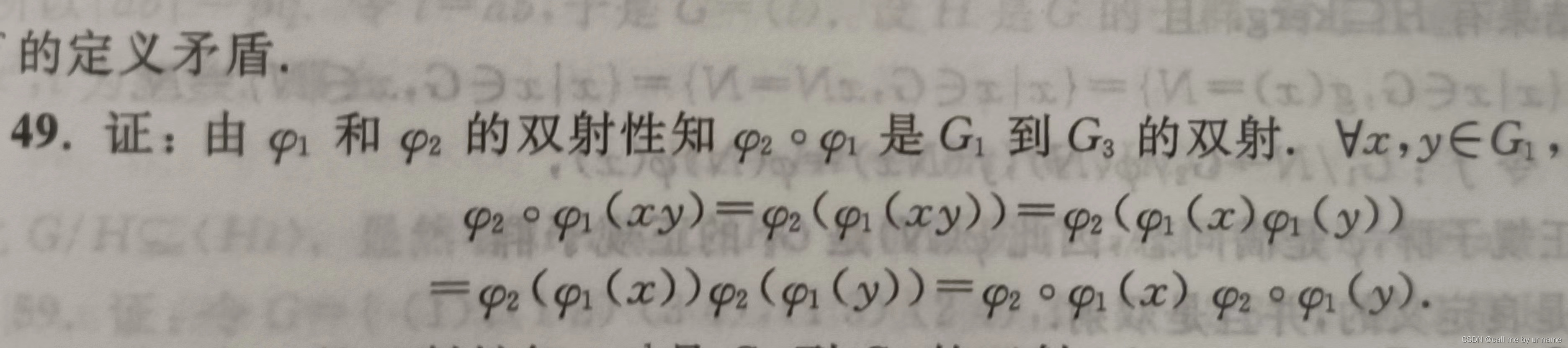
这题比较简单,因为由题意易知,满足双射,所以主要是证明满足同态映射——*(xy)=*'(x)*'(y)(这题就把fai20fai1看作一个运算符)
51题


这题第2问巧啊,有点巧妙,要做对这道题,得能够灵活运用函数的逆,好好看,好好学




 这篇博客介绍了群论的基本概念,包括子群、生成子群、陪集和拉格朗日定理。通过实例解析了置换群和循环群的性质,并探讨了如何判断元素是否为生成元。此外,还涉及到了群的等价关系和同态映射。内容适合数学和理论计算机科学的学生复习使用。
这篇博客介绍了群论的基本概念,包括子群、生成子群、陪集和拉格朗日定理。通过实例解析了置换群和循环群的性质,并探讨了如何判断元素是否为生成元。此外,还涉及到了群的等价关系和同态映射。内容适合数学和理论计算机科学的学生复习使用。








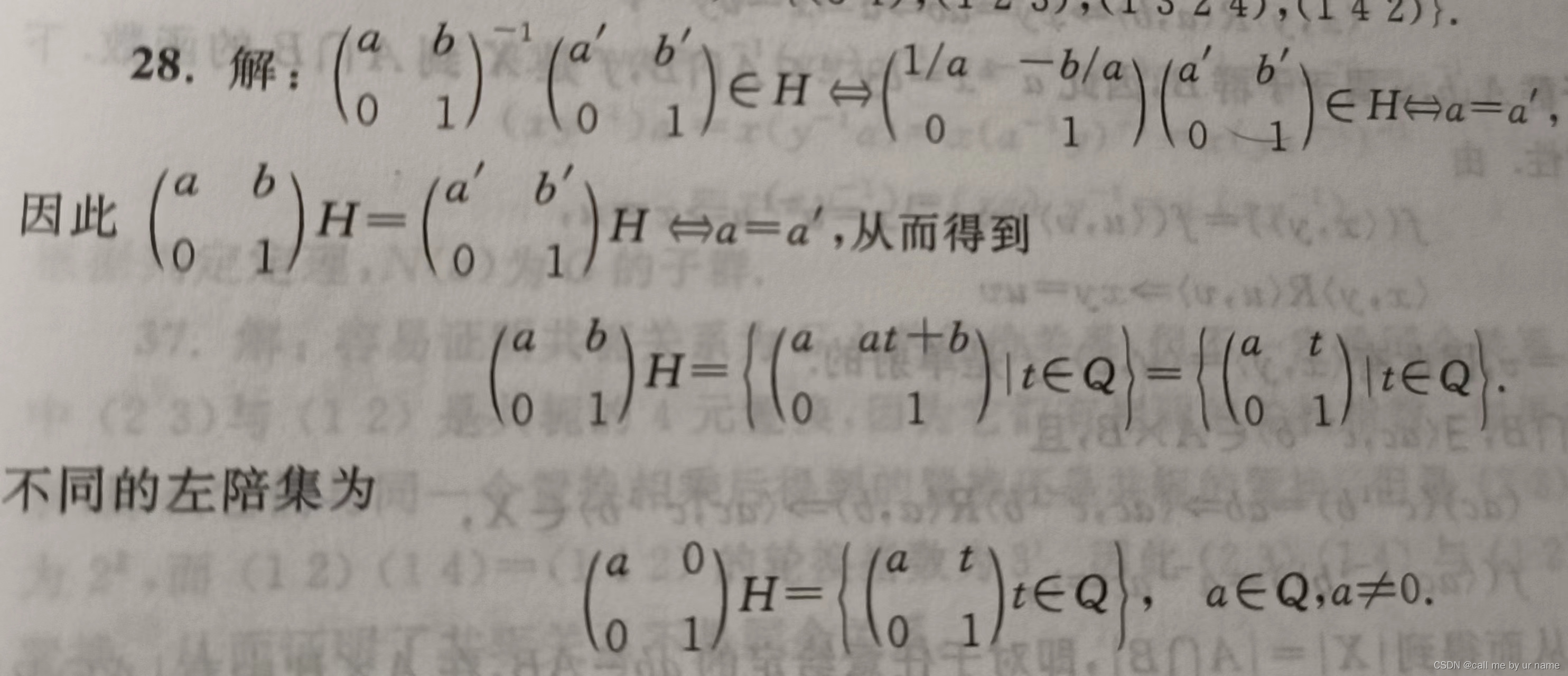
















 1359
1359

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








