头歌计算机组成原理实验—运算器设计(11)第11关：MIPS运算器设计

第11关：MIPS运算器设计

实验目的

学生理解算术逻辑运算单元（ALU）的基本构成，掌握 Logisim 中各种运算组件的使用方法，熟悉多路选择器的使用，能利用前述实验完成的32位加法器、 Logisim 中的运算组件构造指定规格的 ALU 单元。

视频讲解

实验内容

利用前面实验封装好的32位加法器以及 Logisim 平台中现有运算部件，构建一个32位算术逻辑运算单元（禁用 Logisim 系统自带的加法器，减法器），可支持算术加、减、乘、除，逻辑与、或、非、异或运算、逻辑左移、逻辑右移、算术右移运算，支持常用程序状态标志（有符号溢出 OF 、无符号溢出 UOF ，结果相等 Equal ），ALU 功能以及输入输出引脚见后表，在主电路中详细测试自己封装的 ALU ，并分析该运算器的优缺点。

电路框架

alu.circ

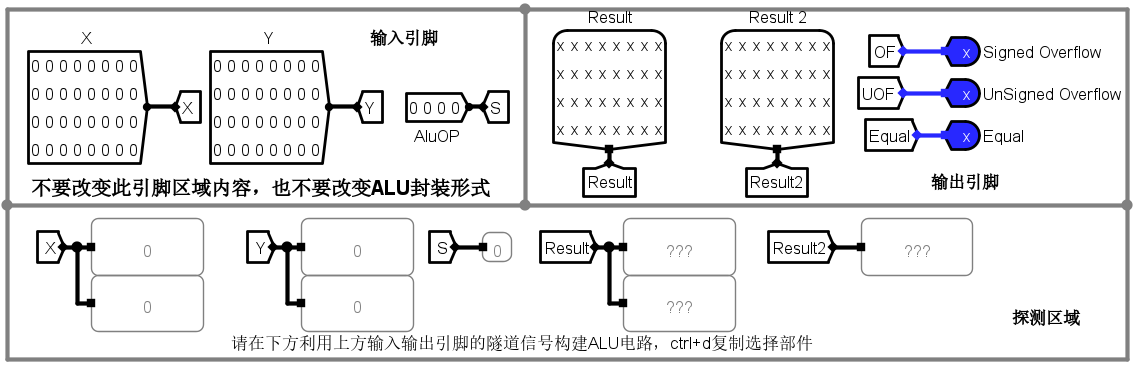
电路引脚

信号	输入/输出	位宽	说明
X	输入	32 位	操作数 X
Y	输入	32 位	操作数 X
ALU_OP	输入	4 位	运算器功能码，具体功能见下表
Result	输出	32 位	ALU 运算结果
Result2	输出	32 位	ALU 结果第二部分，用于乘法指令结果高位或除法指令的余数位，其它运算时值为零
OF	输出	1 位	有符号加减运算溢出标记，其它运算时值为零
UOF	输出	1 位	无符号加减运算溢出标记，其它运算时值为零,溢出条件（加法和小于加数，减法差大于被减数）
Equal	输出	1 位	Equal=(x==y)?1:0, 对所有运算均有效

ALU_OP	十进制	运算功能
0000	0	Result = X << Y 逻辑左移 （Y 取低五位） Result2=0
0001	1	Result = X >>>Y 算术右移 （Y 取低五位） Result2=0
0010	2	Result = X >> Y 逻辑右移 （Y 取低五位） Result2=0
0011	3	Result = (X * Y)[31:0]; Result2 = (X * Y)[63:32] 无符号乘法
0100	4	Result = X/Y; Result2 = X%Y 无符号除法
0101	5	Result = X + Y (Set OF/UOF)
0110	6	Result = X - Y (Set OF/UOF)
0111	7	Result = X & Y 按位与
1000	8	Result = X or Y 按位或
1001	9	Result = X⊕Y 按位异或
1010	10	Result = ~(X orY) 按位或非
1011	11	Result = (X < Y) ? 1 : 0 符号比较
1100	12	Result = (X < Y) ? 1 : 0 无符号比较

电路测试

电路框架提供了自动测试子电路，也可以自行评分，具体测试电路如下图所示：

完成实验后，利用文本编辑工具打开 alu.circ ，将所有文字信息复制粘贴到 Educoder 平台的 alu.circ 文件中，再点击评测按钮即可进行本关测试。平台会对你设计的电路进行自动测试，为方便测试，请勿修改子电路封装，本关测试用例如下:

1. CNT X Y AluOp Result Result2 OF UOF EQ
2. 00 ff00ffff 00000007 0 807fff80 00000000 0 0 0
3. 01 ff00ffff ff00ffff 0 80000000 00000000 0 0 1
4. 02 ff000000 00000018 1 ffffffff 00000000 0 0 0
5. 03 ff00ffff 00000018 2 000000ff 00000000 0 0 0
6. 04 7fffffff 00000010 3 fffffff0 00000007 0 0 0
7. 05 fffffffe 00000010 4 0fffffff 0000000e 0 0 0
8. 06 0000ffff 00000080 5 0001007f 00000000 0 0 0
9. 07 ffffffff ffffffff 5 fffffffe 00000000 0 1 1
10. 08 7fffffff 0000000c 5 8000000b 00000000 1 0 0
11. 09 80000000 80000000 5 00000000 00000000 1 1 1
12. 0a 7ff00000 0000007c 6 7fefff84 00000000 0 0 0
13. 0b 0000007c 7ff00000 6 8010007c 00000000 0 1 0
14. 0c 80000000 00000001 6 7fffffff 00000000 1 0 0
15. 0d 7fffffff fffffffe 6 80000001 00000000 1 1 0
16. 0e ff00ffff 00000018 7 00000018 00000000 0 0 0
17. 0f 7fffffff 00000074 8 7fffffff 00000000 0 0 0

---

开始你的闯关任务吧,升级打怪中....

参考答案：

直接复制代码，字数太多，发不了，后续会上传文件

参考电路图

如果对你有所帮助，感谢点赞加收藏！