灰色预测模型
什么是灰色预测
灰色预测是对既有已知信息和不确定信息的系统进行预测
G M ( 1 , 1 ) 模型 : G r e y M o d e l GM(1,1)模型:Grey Model GM(1,1)模型:GreyModel
GM(1,1)使用原始的离散非负数据,一次累加生成削弱随机性的比较有规律的新的离散数据列,建立微分方程模型,得到近似估计
原理解释
x
(
0
)
=
(
x
(
0
)
(
1
)
,
x
(
0
)
(
2
)
,
.
.
.
,
x
(
0
)
(
n
)
)
是原始数据
,
进行累加之后得到新的数据列
x
(
1
)
(
x
(
0
)
的
1
−
A
G
O
序列
)
(
a
c
c
u
m
u
l
a
t
i
n
g
g
e
n
e
r
a
t
i
o
n
o
p
e
r
a
t
o
r
)
x
(
1
)
=
(
x
(
1
)
(
1
)
,
x
(
1
)
(
2
)
,
.
.
.
,
x
(
1
)
(
n
)
)
x
(
1
)
(
m
)
=
∑
i
=
1
m
x
(
0
)
(
i
)
,
m
=
1
,
2
,
.
.
,
n
再绘制紧邻均值生成数列
z
(
1
)
=
(
z
(
1
)
(
2
)
,
z
(
1
)
(
3
)
,
.
.
.
,
x
(
1
)
(
n
)
)
有
z
(
1
)
(
m
)
=
δ
x
(
1
)
(
m
)
+
(
1
−
δ
)
x
(
1
)
(
m
−
1
)
,
m
=
2
,
.
.
,
n
且
δ
=
0.5
x^{\left( 0 \right)}=\left( x^{\left( 0 \right)}\left( 1 \right) ,x^{\left( 0 \right)}\left( 2 \right) ,...,x^{\left( 0 \right)}\left( n \right) \right) \text{是原始数据},\text{进行累加之后得到新的数据列} \\ x^{\left( 1 \right)}\left( x^{\left( 0 \right)}\text{的}1-AGO\text{序列} \right) \left( accumulating\,\,generation\,\,operator \right) \\ \,\, x^{\left( 1 \right)}=\left( x^{\left( 1 \right)}\left( 1 \right) ,x^{\left( 1 \right)}\left( 2 \right) ,...,x^{\left( 1 \right)}\left( n \right) \right) \\ x^{\left( 1 \right)}\left( m \right) =\sum_{i=1}^m{x^{\left( 0 \right)}\left( i \right) ,m=1,2,..,n} \\ \text{再绘制紧邻均值生成数列} z^{\left( 1 \right)}=\left( z^{\left( 1 \right)}\left( 2 \right) ,z^{\left( 1 \right)}\left( 3 \right) ,...,x^{\left( 1 \right)}\left( n \right) \right) \\ \text{有} z^{\left( 1 \right)}\left( m \right) =\delta x^{\left( 1 \right)}\left( m \right) +\left( 1-\delta \right) x^{\left( 1 \right)}\left( m-1 \right) ,m=2,..,n\text{且}\delta =0.5
x(0)=(x(0)(1),x(0)(2),...,x(0)(n))是原始数据,进行累加之后得到新的数据列x(1)(x(0)的1−AGO序列)(accumulatinggenerationoperator)x(1)=(x(1)(1),x(1)(2),...,x(1)(n))x(1)(m)=i=1∑mx(0)(i),m=1,2,..,n再绘制紧邻均值生成数列z(1)=(z(1)(2),z(1)(3),...,x(1)(n))有z(1)(m)=δx(1)(m)+(1−δ)x(1)(m−1),m=2,..,n且δ=0.5
设计离散型微分方程
x
(
0
)
(
k
)
+
a
z
(
1
)
(
k
)
=
b
x^{\left( 0 \right)}\left( k \right) +az^{\left( 1 \right)}\left( k \right) =b
x(0)(k)+az(1)(k)=b,其中
b
b
b是灰作用量,
−
a
-a
−a表示发展系数
根据上面的式子
x
(
0
)
=
(
x
(
0
)
(
1
)
,
x
(
0
)
(
2
)
,
.
.
.
,
x
(
0
)
(
n
)
)
x^{\left( 0 \right)}=\left( x^{\left( 0 \right)}\left( 1 \right) ,x^{\left( 0 \right)}\left( 2 \right) ,...,x^{\left( 0 \right)}\left( n \right) \right)
x(0)=(x(0)(1),x(0)(2),...,x(0)(n))
可以知道通过矩阵的形式写成
u
=
(
a
,
b
)
T
,
Y
=
[
x
(
0
)
(
2
)
x
(
0
)
(
3
)
⋮
x
(
0
)
(
n
)
]
,
B
=
[
−
z
(
1
)
(
2
)
1
−
z
(
1
)
(
3
)
1
⋮
−
z
(
1
)
(
n
)
1
]
u=\left( a,b \right) ^T,Y=\left[ \begin{array}{c} x^{\left( 0 \right)}\left( 2 \right)\\ x^{\left( 0 \right)}\left( 3 \right)\\ \vdots\\ x^{\left( 0 \right)}\left( \begin{array}{c} n\\ \end{array} \right)\\ \end{array} \right] ,B=\left[ \begin{array}{c} -z^{\left( 1 \right)}\left( 2 \right) \,\,1\\ -z^{\left( 1 \right)}\left( 3 \right) \,\,1\\ \vdots\\ -z^{\left( 1 \right)}\left( n \right) \,\,1\\ \end{array} \right]
u=(a,b)T,Y=⎣
⎡x(0)(2)x(0)(3)⋮x(0)(n)⎦
⎤,B=⎣
⎡−z(1)(2)1−z(1)(3)1⋮−z(1)(n)1⎦
⎤
将式子改写称为
Y
=
B
u
Y=Bu
Y=Bu
使用最小二乘法得到a,b的估计值
u
^
=
(
a
^
b
^
)
=
(
B
T
B
)
−
1
B
T
Y
\hat{u}=\left( \begin{array}{c} \hat{a}\\ \hat{b}\\ \end{array} \right) =\left( B^TB \right) ^{-1}B^TY
u^=(a^b^)=(BTB)−1BTY
可以将累次序列
x
(
0
)
x^{\left( 0 \right)}
x(0)看作因变量,将
z
(
1
)
z^{\left( 1 \right)}
z(1)视为自变量
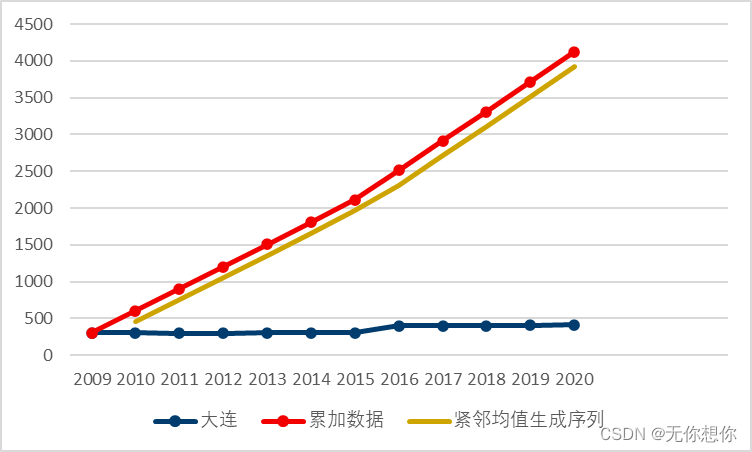
画出数据对应的图像
以2022年辽宁省省赛的数据为例绘制如下图像
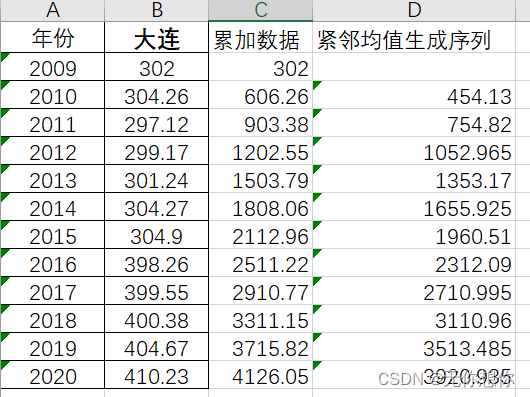
画出如下图像
最小二乘法OLS的介绍
y
i
=
k
x
i
+
b
+
u
i
k
^
,
b
^
=
arg
min
k
,
b
u
^
i
2
=
arg
min
k
,
b
∑
i
=
1
n
(
y
i
−
k
x
i
−
b
)
2
令
L
=
∑
i
=
1
n
(
y
i
−
k
x
i
−
b
)
2
=
[
y
1
−
k
x
1
−
b
,
y
2
−
k
x
2
−
b
,
⋯
,
y
n
−
k
x
n
−
b
]
[
y
1
−
k
x
1
−
b
y
2
−
k
x
2
−
b
⋮
y
n
−
k
x
n
−
b
]
\begin{array}{c} \begin{array}{l} y_{i}=k x_{i}+b+u_{i} \\ \hat{k}, \hat{b}=\underset{k, b}{\arg \min } \hat{u}_{i}^{2}=\underset{k, b}{\arg \min } \sum_{i=1}^{n}\left(y_{i}-k x_{i}-b\right)^{2} \\ \text { 令 } L=\sum_{i=1}^{n}\left(y_{i}-k x_{i}-b\right)^{2}=\left[y_{1}-k x_{1}-b, y_{2}-k x_{2}-b, \cdots, y_{n}-k x_{n}-b\right]\left [\begin{array}{c} y_{1}-k x_{1}-b \\ y_{2}-k x_{2}-b \\ \vdots \\ y_{n}-k x_{n}-b \end{array}\right] \end{array} \end{array}
yi=kxi+b+uik^,b^=k,bargminu^i2=k,bargmin∑i=1n(yi−kxi−b)2 令 L=∑i=1n(yi−kxi−b)2=[y1−kx1−b,y2−kx2−b,⋯,yn−kxn−b]⎣
⎡y1−kx1−by2−kx2−b⋮yn−kxn−b⎦
⎤
L
=
(
Y
−
X
β
)
T
(
Y
−
X
β
)
=
(
Y
T
−
β
T
X
T
)
(
Y
−
X
β
)
=
Y
T
Y
−
Y
T
X
β
−
β
T
X
T
Y
+
β
T
X
T
X
β
则
β
^
=
[
b
^
k
^
]
=
a
r
g
min
β
(
Y
T
Y
−
Y
T
X
β
−
β
T
X
T
Y
+
β
T
X
T
X
β
)
L=(Y-X\beta )^T(Y-X\beta )\ \\ \,\, \begin{array}{l} \,\ \,\ \,\ \,\ \,\ =\left( Y^T-\beta ^TX^T \right) (Y-X\beta )\\ \,\ =Y^TY-Y^TX\beta -\beta ^TX^TY+\beta ^TX^TX\beta\\ \end{array} \\ 则\widehat{\beta }=\left[ \begin{array}{l} \hat{b}\\ \hat{k}\\ \end{array} \right] =\underset{\beta}{\mathrm{arg}\min}\left( Y^TY-Y^TX\beta -\beta ^TX^TY+\beta ^TX^TX\beta \right)
L=(Y−Xβ)T(Y−Xβ) =(YT−βTXT)(Y−Xβ) =YTY−YTXβ−βTXTY+βTXTXβ则β
=[b^k^]=βargmin(YTY−YTXβ−βTXTY+βTXTXβ)
∂ L ∂ β = − X T Y − X T Y + 2 X T X β = 0 ⇒ X T X β = X T Y 转换位置以后可以得到 β ^ = ( X T X ) − 1 X T Y \frac{\partial L}{\partial \beta}=-X^TY-X^TY+2X^TX\beta =0\Rightarrow X^TX\beta =X^TY \\转换位置以后可以得到 \widehat{\beta }=\left( X^TX \right) ^{-1}X^TY ∂β∂L=−XTY−XTY+2XTXβ=0⇒XTXβ=XTY转换位置以后可以得到β =(XTX)−1XTY
这里我们需要注意到的是
(
X
T
X
)
\left( X^TX \right)
(XTX)是可逆的,那么就必须保证X的列向量都是线性无关的,不然会出现完全多重共线性的问题
之后将
β
^
\widehat{\beta }
β
带入式子便可以得到
a
^
\widehat{a}
a
和
b
^
\widehat{b}
b
的值
GM(1,1)原理介绍
根据 O L S 估计得到 a ^ 和 b ^ , 即 x ( 0 ) ( k ) = − a ^ z ( 1 ) ( k ) + b ^ ( k = 2 , 3 , ⋯ , n ) x ( 0 ) ( k ) = − a ^ z ( 1 ) ( k ) + b ^ ⇒ x ( 1 ) ( k ) − x ( 1 ) ( k − 1 ) = − a ^ z ( 1 ) ( k ) + b ^ x ( 1 ) ( k ) − x ( 1 ) ( k − 1 ) = ∫ k − 1 k d x ( 1 ) ( t ) d t d t ( 牛顿 − 莱布尼茨公式 ) z ( 1 ) ( k ) = x ( 1 ) ( k ) + x ( 1 ) ( k − 1 ) 2 ≈ ∫ k − 1 k x ( 1 ) ( t ) d t ( 定积分的几何意义 ) 根据OLS估计得到 \hat{a} 和 \hat{b} , 即 x^{(0)}(k)=-\hat{a} z^{(1)}(k)+\hat{b} \quad(k=2,3, \cdots, n) \\x^{(0)}(k)=-\hat{a} z^{(1)}(k)+\hat{b} \Rightarrow x^{(1)}(k)-x^{(1)}(k-1) \\\\\\=-\hat{a} z^{(1)}(k)+\hat{b} x^{(1)}(k)-x^{(1)}(k-1)=\int_{k-1}^{k} \frac{d x^{(1)}(t)}{d t} d t (牛顿-莱布尼茨公式 ) \\ z^{(1)}(k)=\frac{x^{(1)}(k)+x^{(1)}(k-1)}{2} \approx \int_{k-1}^{k} x^{(1)}(t) d t (定积分的几何意义) 根据OLS估计得到a^和b^,即x(0)(k)=−a^z(1)(k)+b^(k=2,3,⋯,n)x(0)(k)=−a^z(1)(k)+b^⇒x(1)(k)−x(1)(k−1)=−a^z(1)(k)+b^x(1)(k)−x(1)(k−1)=∫k−1kdtdx(1)(t)dt(牛顿−莱布尼茨公式)z(1)(k)=2x(1)(k)+x(1)(k−1)≈∫k−1kx(1)(t)dt(定积分的几何意义)
∫
k
−
1
k
d
x
(
1
)
(
t
)
d
t
d
t
≈
−
a
^
∫
k
−
1
k
x
(
1
)
(
t
)
d
t
+
∫
k
−
1
k
b
^
d
t
=
∫
k
−
1
k
[
−
a
^
x
(
1
)
(
t
)
+
b
^
]
d
t
微分方程
:
d
x
(
1
)
(
t
)
d
t
=
−
a
^
x
(
1
)
(
t
)
+
b
^
被称为
GM
(
1
,
1
)
模型的白化方程
x
(
0
)
(
k
)
+
a
z
(
1
)
(
k
)
=
b
(
GM
(
1
,
1
)
模型的基本形式
)
则被称为灰色微分方程
\begin{aligned} \int_{k-1}^{k} \frac{d x^{(1)}(t)}{d t} d t & \approx-\hat{a} \int_{k-1}^{k} x^{(1)}(t) d t+\int_{k-1}^{k} \hat{b} d t \\ &=\int_{k-1}^{k}\left[-\hat{a} x^{(1)}(t)+\hat{b}\right] d t \end{aligned} \\微分方程: \frac{d x^{(1)}(t)}{d t}=-\hat{a} x^{(1)}(t)+\hat{b} 被称为 \operatorname{GM}(1,1) 模型的白化方程 \\ x^{(0)}(k)+a z^{(1)}(k)=b(\operatorname{GM}(1,1) 模型的基本形式 ) 则被称为灰色微分方程
∫k−1kdtdx(1)(t)dt≈−a^∫k−1kx(1)(t)dt+∫k−1kb^dt=∫k−1k[−a^x(1)(t)+b^]dt微分方程:dtdx(1)(t)=−a^x(1)(t)+b^被称为GM(1,1)模型的白化方程x(0)(k)+az(1)(k)=b(GM(1,1)模型的基本形式)则被称为灰色微分方程
这里所提到的白化方程可以理解为是白噪声(即没有扰动项)的意思
提出灰色微分方程这样一个概念,主要是为了解决信息不完备的系统的问题,建立近似的微分方程
白化方程
:
d
x
(
1
)
(
t
)
d
t
=
−
a
^
x
(
1
)
(
t
)
+
b
^
如果我们取初始值
x
^
(
1
)
(
t
)
∣
t
=
1
=
x
(
0
)
(
1
)
,
我们可以求出其对应的解为
:
x
^
(
1
)
(
t
)
=
[
x
(
0
)
(
1
)
−
b
^
a
^
]
e
−
a
^
(
t
−
1
)
+
b
^
a
^
所以
x
^
(
1
)
(
m
+
1
)
=
[
x
(
0
)
(
1
)
−
b
^
a
^
]
e
−
a
^
m
+
b
^
a
^
,
m
=
1
,
2
,
⋯
,
n
−
1
白化方程: \frac{d x^{(1)}(t)}{d t}=-\hat{a} x^{(1)}(t)+\hat{b} 如果我们取初始值 \\ \left.\hat{x}^{(1)}(t)\right|_{t=1}=x^{(0)}(1) , \\ 我们可以求出其对应的解为: \\ \hat{x}^{(1)}(t)=\left[x^{(0)}(1)-\frac{\hat{b}}{\hat{a}}\right] e^{-\hat{a}(t-1)}+\frac{\hat{b}}{\hat{a}} \\\,\ \text { 所以 } \hat{x}^{(1)}(m+1)=\left[x^{(0)}(1)-\frac{\hat{b}}{\hat{a}}\right] e^{-\hat{a} m}+\frac{\hat{b}}{\hat{a}}, m=1,2, \cdots, n-1
白化方程:dtdx(1)(t)=−a^x(1)(t)+b^如果我们取初始值x^(1)(t)∣
∣t=1=x(0)(1),我们可以求出其对应的解为:x^(1)(t)=[x(0)(1)−a^b^]e−a^(t−1)+a^b^ 所以 x^(1)(m+1)=[x(0)(1)−a^b^]e−a^m+a^b^,m=1,2,⋯,n−1
一次微分方程
一阶齐次线性方程组
形如
d
y
d
x
+
P
(
x
)
y
=
0
的方程称为一阶齐次线性微分方程
,
其通解公式为
:
y
=
C
e
−
∫
P
(
x
)
d
x
形如 \frac{d y}{d x}+P(x) y=0 的方程称为一阶齐次线性微分方程, 其通解公式为: \\y=C e^{-\int P(x) d x}
形如dxdy+P(x)y=0的方程称为一阶齐次线性微分方程,其通解公式为:y=Ce−∫P(x)dx
一阶非齐次线性微分方程
形如
d
y
d
x
+
P
(
x
)
y
=
Q
(
x
)
的方程称为一阶非齐次线性微分方程
,
其通解公式为
:
y
=
[
∫
Q
(
x
)
e
∫
P
(
x
)
d
x
d
x
+
C
]
e
−
∫
P
(
x
)
d
x
形如 \frac{d y}{d x}+P(x) y=Q(x) 的方程称为一阶非齐次线性微分方程, 其通解公式为: \\ y=\left[\int Q(x) e^{\int P(x) d x} d x+C\right] e^{-\int P(x) d x}
形如dxdy+P(x)y=Q(x)的方程称为一阶非齐次线性微分方程,其通解公式为:y=[∫Q(x)e∫P(x)dxdx+C]e−∫P(x)dx
根据上述的微分方程的使用,我们就可以理解并使用
G
M
(
1
,
1
)
GM(1,1)
GM(1,1)来进行预测
根据
x
(
1
)
(
m
)
=
∑
i
=
1
m
x
(
0
)
(
i
)
,
m
=
1
,
2
,
⋯
,
n
,
我们可以有
x
^
(
0
)
(
m
+
1
)
=
x
^
(
1
)
(
m
+
1
)
−
x
^
(
1
)
(
m
)
=
(
1
−
e
a
^
)
[
x
(
0
)
(
1
)
−
b
^
a
^
]
e
−
a
^
m
,
m
=
1
,
2
,
⋯
,
n
−
1
根据 x^{(1)}(m)=\sum_{i=1}^{m} x^{(0)}(i), m=1,2, \cdots, n , \\ 我们可以有 \\ \hat{x}^{(0)}(m+1)=\hat{x}^{(1)}(m+1)-\hat{x}^{(1)}(m)=\left(1-e^{\hat{a}}\right)\left[x^{(0)}(1)-\frac{\hat{b}}{\hat{a}}\right] e^{-\hat{a} m}, m=1,2, \cdots, n-1
根据x(1)(m)=i=1∑mx(0)(i),m=1,2,⋯,n,我们可以有x^(0)(m+1)=x^(1)(m+1)−x^(1)(m)=(1−ea^)[x(0)(1)−a^b^]e−a^m,m=1,2,⋯,n−1
注意到
x
^
(
1
)
(
m
+
1
)
−
x
^
(
1
)
(
m
)
\hat{x}^{(1)}(m+1)-\hat{x}^{(1)}(m)
x^(1)(m+1)−x^(1)(m)这个式子,根据图像的描述可以写成
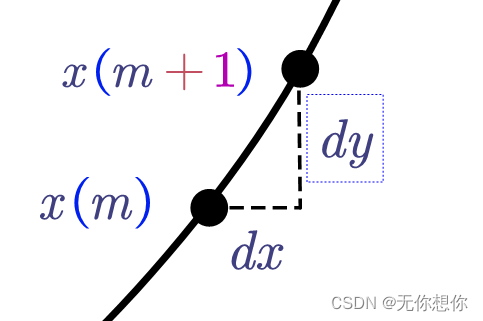
这个式子就和一次微分方程的计算方法相关,也是灰色预测的作用的具体展示,表明了灰色预测是根据前一个值进行预测的,比如说要预测
x
(
m
+
2
)
x(m+2)
x(m+2)这个值,那么就需要有
x
(
m
+
1
)
x(m+1)
x(m+1)这样的一个数据,可以理解为做差
G
M
(
1
,
1
)
模型是有条件的指数拟合
:
f
(
x
)
=
C
1
e
C
2
(
x
−
1
)
GM(1,1)模型是有条件的指数拟合:f(x)=C_{1} e^{C_{2}(x-1)}
GM(1,1)模型是有条件的指数拟合:f(x)=C1eC2(x−1)
准指数规律检验
(
1
)
数据具有准指数规律是使用灰色系统建模的理论基础。
(
2
)
累加
r
次的序列为
:
x
(
r
)
=
(
x
(
r
)
(
1
)
,
x
(
r
)
(
2
)
,
⋯
,
x
(
r
)
(
n
)
)
,
定义级比
σ
(
k
)
=
x
(
r
)
(
k
)
x
(
r
)
(
k
−
1
)
,
k
=
2
,
3
,
⋯
,
n
.
(
3
)
如果
∀
k
,
σ
(
k
)
∈
[
a
,
b
]
,
且区间长度
δ
=
b
−
a
<
0.5
,
则称累加
r
次后的序列具有准指数规律。
(
4
)
具体到
GM
(
1
,
1
)
模型中
,
我们只需要判断累加一次后的序列
x
(
1
)
=
(
x
(
1
)
(
1
)
,
x
(
1
)
(
2
)
,
⋯
,
x
(
1
)
(
n
)
)
是否具有准指数规律。
(
5
)
根据上述公式
:
序列
x
(
1
)
的级比
σ
(
k
)
=
x
(
1
)
(
k
)
x
(
1
)
(
k
−
1
)
=
x
(
0
)
(
k
)
+
x
(
1
)
(
k
−
1
)
x
(
1
)
(
k
−
1
)
=
x
(
0
)
(
k
)
x
(
1
)
(
k
−
1
)
+
1
,
定义
ρ
(
k
)
=
x
(
0
)
(
k
)
x
(
1
)
(
k
−
1
)
为原始序列
x
(
0
)
的光滑比
,
注意到
ρ
(
k
)
=
x
(
0
)
(
k
)
x
(
0
)
(
1
)
+
x
(
0
)
(
2
)
+
⋯
+
x
(
0
)
(
k
−
1
)
,
假设
x
(
0
)
为非负序列(生活中的常见的时间序列几乎都满足非负性),
那么随着
k
增加
,
最终
ρ
(
k
)
会逐渐接近
0
,
因此要使得具有
x
(
1
)
具有准指数规律
,
即
∀
k
,
区间长度
δ
<
0.5
,
只需要只需要保证
ρ
(
k
)
∈
(
0
,
0.5
)
即可
,
此时序列
x
(
1
)
的级比
σ
(
k
)
∈
(
1
,
1.5
)
.
(1) 数据具有准指数规律是使用灰色系统建模的理论基础。 \\(2) 累加 r 次的序列为: x^{(r)}=\left(x^{(r)}(1), x^{(r)}(2), \cdots, x^{(r)}(n)\right) , 定义级比 \sigma(k)=\frac{x^{(r)}(k)}{x^{(r)}(k-1)}, k=2,3, \cdots, n . \\(3) 如果 \forall k, \sigma(k) \in[a, b] , 且区间长度 \delta=b-a<0.5 , 则称累加 r 次后的序列具有准指数规律。 \\(4) 具体到 \operatorname{GM}(1,1) 模型中, 我们只需要判断累加一次后的序列 x^{(1)}=\left(x^{(1)}(1), x^{(1)}(2), \cdots, x^{(1)}(n)\right) 是否 具有准指数规律。 \\(5) 根据上述公式: 序列 x^{(1)} 的级比 \sigma(k)=\frac{x^{(1)}(k)}{x^{(1)}(k-1)}=\frac{x^{(0)}(k)+x^{(1)}(k-1)}{x^{(1)}(k-1)}=\frac{x^{(0)}(k)}{x^{(1)}(k-1)}+1 , \\定义 \rho(k)=\frac{x^{(0)}(k)}{x^{(1)}(k-1)} 为原始序列 x^{(0)} 的光滑比, \\注意到\rho(k)= \frac{x^{(0)}(k)}{x^{(0)}(1)+x^{(0)}(2)+\cdots+x^{(0)}(k-1)} , \\假设 x^{(0)} 为非负序列(生活中的常见的时间序列几乎都满足非负性), \\那么随着 k 增加, 最终 \rho(k) 会逐渐接近 0 , 因此要使得具有 x^{(1)} 具有准指数规律, \\即 \forall k , 区间长度 \delta<0.5 , 只需要只需要保证 \rho(k) \in(0,0.5) 即可, 此 时序列 x^{(1)} 的级比 \sigma(k) \in(1,1.5) .
(1)数据具有准指数规律是使用灰色系统建模的理论基础。(2)累加r次的序列为:x(r)=(x(r)(1),x(r)(2),⋯,x(r)(n)),定义级比σ(k)=x(r)(k−1)x(r)(k),k=2,3,⋯,n.(3)如果∀k,σ(k)∈[a,b],且区间长度δ=b−a<0.5,则称累加r次后的序列具有准指数规律。(4)具体到GM(1,1)模型中,我们只需要判断累加一次后的序列x(1)=(x(1)(1),x(1)(2),⋯,x(1)(n))是否具有准指数规律。(5)根据上述公式:序列x(1)的级比σ(k)=x(1)(k−1)x(1)(k)=x(1)(k−1)x(0)(k)+x(1)(k−1)=x(1)(k−1)x(0)(k)+1,定义ρ(k)=x(1)(k−1)x(0)(k)为原始序列x(0)的光滑比,注意到ρ(k)=x(0)(1)+x(0)(2)+⋯+x(0)(k−1)x(0)(k),假设x(0)为非负序列(生活中的常见的时间序列几乎都满足非负性),那么随着k增加,最终ρ(k)会逐渐接近0,因此要使得具有x(1)具有准指数规律,即∀k,区间长度δ<0.5,只需要只需要保证ρ(k)∈(0,0.5)即可,此时序列x(1)的级比σ(k)∈(1,1.5).
(以上内容再取自清风数学建模老师的ppt)
(摘取自
刘思峰, 谢乃明, 等. 2010. 灰色系统理论及其应用
[
M
]
.
5
版. 北京: 科学出版社
\text { 刘思峰, 谢乃明, 等. 2010. 灰色系统理论及其应用 }[M] .5 \text { 版. 北京: 科学出版社 }
刘思峰, 谢乃明, 等. 2010. 灰色系统理论及其应用 [M].5 版. 北京: 科学出版社 )
在数据当中,我们一般比较关注后期的期数,因为在数据不断增加之后,那么预测出来的结果也会更加精确
书本上对发展系数与预测情形的探究如下
GM
(
1
,
1
)
适用情况和发展系数的大小有很大关系
,
教材中给了如下结论
:
当
∣
a
∣
>
2
时
,
模型没有意义
;
当
∣
a
∣
<
2
时
,
GM
(
1
,
1
)
才有意义。
当
a
取不同值时
,
预测的最终效果也不相同
,
具体讨论如下
:
当
−
a
<
0.3
时
,
G
M
(
1
,
1
)
模型适合于中期和长期数据的预测。
当
0.3
<
−
a
⩽
0.5
时
,
GM
(
1
,
1
)
模型适合于短期预测
,
中长期数据预测应谨慎使用。
当
0.5
<
−
a
⩽
0.8
时
,
GM
(
1
,
1
)
模型对于预测短期数据应谨慎使用。
当
0.8
<
−
a
⩽
1.0
时
,
应对
GM
(
1
,
1
)
进行残差修正
(
见教材
)
后使用。
当
−
a
>
1
时
,
不宜使用
G
M
(
1
,
1
)
模型进行预测。
所以
,
我们可以根据预测出的
a
^
.
来和上述范围比较
,
来确定适用情况。
\operatorname{GM}(1,1) 适用情况和发展系数的大小有很大关系, 教材中给了如下结论: \\ 当 |a|>2 时, 模型没有意义; \\当 |a|<2 时, \operatorname{GM}(1,1) 才有意义。 \\当 a 取不同值时, 预测的最终效果也不相同, 具体讨论如下: \\当 -a<0.3 时, \mathrm{GM}(1,1) 模型适合于中期和长期数据的预测。 \\ 当 0.3<-a \leqslant 0.5 时, \operatorname{GM}(1,1) 模型适合于短期预测, 中长期数据预测应谨慎使用。 \\ 当 0.5<-a \leqslant 0.8 时, \operatorname{GM}(1,1) 模型对于预测短期数据应谨慎使用。 \\ 当 0.8<-a \leqslant 1.0 时, 应对 \operatorname{GM}(1,1) 进行残差修正(见教材)后使用。 \\当 -a>1 时, 不宜使用 \mathrm{GM}(1,1) 模型进行预测。 \\ 所以, 我们可以根据预测出的 \widehat{a} . 来和上述范围比较, 来确定适用情况。
GM(1,1)适用情况和发展系数的大小有很大关系,教材中给了如下结论:当∣a∣>2时,模型没有意义;当∣a∣<2时,GM(1,1)才有意义。当a取不同值时,预测的最终效果也不相同,具体讨论如下:当−a<0.3时,GM(1,1)模型适合于中期和长期数据的预测。当0.3<−a⩽0.5时,GM(1,1)模型适合于短期预测,中长期数据预测应谨慎使用。当0.5<−a⩽0.8时,GM(1,1)模型对于预测短期数据应谨慎使用。当0.8<−a⩽1.0时,应对GM(1,1)进行残差修正(见教材)后使用。当−a>1时,不宜使用GM(1,1)模型进行预测。所以,我们可以根据预测出的a
.来和上述范围比较,来确定适用情况。
上诉结论告诉我们发展系数越小预测的越精确
GM(1,1)模型检验
对模型使用的时候其数值的拟合优度是否高效,可以使用如下办法(以下检验方法都是摘取自上述课程和书本)
残差检验
绝对残差 : ε ( k ) = x ( 0 ) ( k ) − x ^ ( 0 ) ( k ) , k = 2 , 3 , ⋯ , n 相对残差 : ε r ( k ) = ∣ x ( 0 ) ( k ) − x ^ ( 0 ) ( k ) ∣ x ( 0 ) ( k ) × 100 % , k = 2 , 3 , ⋯ , n 平均相对残差 : ε ˉ r = 1 n − 1 ∑ k = 2 n ∣ ε r ( k ) ∣ 如果 ε ˉ r < 20 % , 则认为 G M ( 1 , 1 ) 对原数据的拟合达到一般要求。 如果 ε ˉ r < 10 % , 则认为 G M ( 1 , 1 ) 对原数据的拟合效果非常不错。 注 : ( 1 ) 残差检验可以适用于其他预测模型 ( 2 ) 关于这个 10 % 和 20 % 的标准不是绝对的 , 可以根据题目的需要进行修改 . 绝对残差: \varepsilon(k)=x^{(0)}(k)-\widehat{x}^{(0)}(k), k=2,3, \cdots, n \\相对残差: \varepsilon_{r}(k)=\frac{\left|x^{(0)}(k)-\widehat{x}^{(0)}(k)\right|}{x^{(0)}(k)} \times 100 \%, k=2,3, \cdots, n \\平均相对残差: \bar{\varepsilon}_{r}=\frac{1}{n-1} \sum_{k=2}^{n}\left|\varepsilon_{r}(k)\right| \\ 如果 \bar{\varepsilon}_{r}<20 \% , 则认为 G M(1,1) 对原数据的拟合达到一般要求。 \\如果 \bar{\varepsilon}_{r}<10 \% , 则认为 G M(1,1) 对原数据的拟合效果非常不错。 \\注:(1)残差检验可以适用于其他预测模型 \,\\(2) 关于这个 10 \% 和 20 \% 的标准不是绝对的, 可以根据题目的需要进行修改. 绝对残差:ε(k)=x(0)(k)−x (0)(k),k=2,3,⋯,n相对残差:εr(k)=x(0)(k)∣x(0)(k)−x (0)(k)∣×100%,k=2,3,⋯,n平均相对残差:εˉr=n−11∑k=2n∣εr(k)∣如果εˉr<20%,则认为GM(1,1)对原数据的拟合达到一般要求。如果εˉr<10%,则认为GM(1,1)对原数据的拟合效果非常不错。注:(1)残差检验可以适用于其他预测模型(2)关于这个10%和20%的标准不是绝对的,可以根据题目的需要进行修改.
级比偏差检验
首先由
x
(
0
)
(
k
−
1
)
和
x
(
0
)
(
k
)
计算出原始数据的级比
σ
(
k
)
:
首先由 x^{(0)}(k-1) 和 x^{(0)}(k) 计算出原始数据的级比 \sigma(k) :
首先由x(0)(k−1)和x(0)(k)计算出原始数据的级比σ(k):
σ
(
k
)
=
x
(
0
)
(
k
)
x
(
0
)
(
k
−
1
)
(
k
=
2
,
3
,
⋯
,
n
)
\sigma(k)=\frac{x^{(0)}(k)}{x^{(0)}(k-1)}(k=2,3, \cdots, n)
σ(k)=x(0)(k−1)x(0)(k)(k=2,3,⋯,n)
再根据预测出来的发展系数
(
−
a
^
)
计算出相应的级比偏差和平均级比偏差
:
再根据预测出来的发展系数 (-\widehat{a}) 计算出相应的级比偏差和平均级比偏差:
再根据预测出来的发展系数(−a
)计算出相应的级比偏差和平均级比偏差:
η
(
k
)
=
∣
1
−
1
−
0.5
a
^
1
+
0.5
a
^
1
σ
(
k
)
∣
,
η
ˉ
=
∑
k
=
2
n
η
(
k
)
/
(
n
−
1
)
\\ \eta(k)=\left|1-\frac{1-0.5 \hat{a}}{1+0.5 \hat{a}} \frac{1}{\sigma(k)}\right|, \bar{\eta}=\sum_{k=2}^{n} \eta(k) /(n-1)
η(k)=∣
∣1−1+0.5a^1−0.5a^σ(k)1∣
∣,ηˉ=k=2∑nη(k)/(n−1)
如果
η
ˉ
<
0.2
,
则认为
G
M
(
1
,
1
)
对原数据的拟合达到一般要求。
如果
η
ˉ
<
0.1
,
则认为
G
M
(
1
,
1
)
对原数据的拟合效果非常不错。
\\如果 \bar{\eta}<0.2 , 则认为 G M(1,1) 对原数据的拟合达到一般要求。 \\ 如果 \bar{\eta}<0.1 , 则认为 GM(1,1) 对原数据的拟合效果非常不错。
如果ηˉ<0.2,则认为GM(1,1)对原数据的拟合达到一般要求。如果ηˉ<0.1,则认为GM(1,1)对原数据的拟合效果非常不错。
η
ˉ
\bar{\eta}
ηˉ越小,说明差距越小,也就说明了拟合优度很强
GM(1,1)的拓展
书本的截图

总结为
- 全数据 G M ( 1 , 1 ) GM(1,1) GM(1,1)
- 部分数据 G M ( 1 , 1 ) GM(1,1) GM(1,1)
- 新信息 G M ( 1 , 1 ) GM(1,1) GM(1,1)
- 新陈代谢
G
M
(
1
,
1
)
GM(1,1)
GM(1,1)
目前来看新陈代谢 G M ( 1 , 1 ) GM(1,1) GM(1,1)在大部分预测当中预测效果是最好的,它的使用原理也是比较符合和理想的
什么时候使用灰色预测
大家可以多个方法进行预测,然后使用同一个检验方法来检验那一个使用效率是最高的,然后就可以写入到论文当中,清风老师的看法如下
- 数据是以年份度量的非负数据(如果是月份或者季度数据使用时间序列模型)
- 数据能经过准指数规律的检验(除了前两期外, 后面 至少 90 % 的期数的光滑比要低于 0.5 )
- 数据的期数较短且和其他数据之间的关联性不强(小 于等于 10 , 也不能太短了, 比如只有 3 期数据), 要是数据 期数较长, 一般用传统的时间序列模型比较合适。






















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








