机器学习-逻辑回归算法

逻辑回归算法的名字虽然带有“回归”二字，但实际上逻辑回归算法是用来解决分类问题的算法。

1.预测函数

需要找出 一个预测函数模型，使其值输出在[0,1]之间。然后选择一个基准值，如0.5，如果算出来的预测值大于0.5，就认为其预测值为1，反之则其预测值为0。
选择Sigmoid 函数:$$g(z)=\frac{1}{1+e^{-z}}$$
也称为Logistic函数。

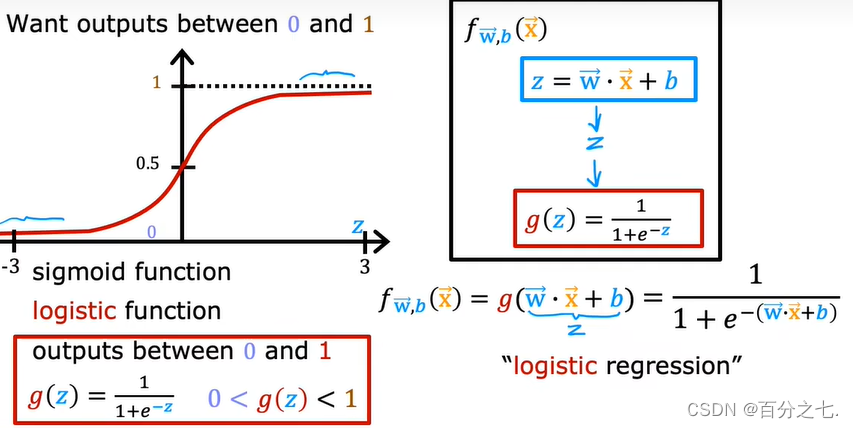
从图中可以看出，Sigmoid函数是一个S型的曲线，它的取值在[0,1]之间，在远离0的地方函数值会很快接近0或1。一个事件发生的概率是在0到1之间的，每一个概率都可以映射到函数的某一个值上，就可以归类为超过50%的概率更容易实现归一为1，低于50%的概率更不容易实现归一为0，这样就存在了只有0/1的二分类问题。

2.判定边界

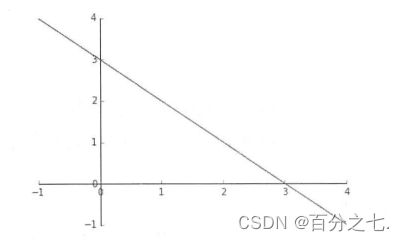
假定有两个变量x1,x2,其逻辑回归预测函数是$$h_{\theta }(x)=g\left({\mathbf{\theta }}_0+{\mathbf{\theta }}_1{x}_1+{\mathbf{\theta }}_2{x}_2\right)$$假设给定参数：$$\theta =\left[\begin{array}{c}-3\\ 1\\ 1\end{array}\right]$$那么可以得到判定边界-3+x1+x2=0，即x1+x2=3，如果以x1为横坐标,x2为纵坐标，则这个函数画出来就是一个通过(0,3)和(3,0)两个点的斜线。这条线就是判定边界。

3.成本函数

我们不能使用线性回归模型的成本函数来推导逻辑回归的成本函数，因为那样的成本函数太复杂，最终很可能会导致无法通过法代找到成本函数值最小的点。
为了容易地求出成本函数的最小值，我们分成 y=1和y=0两种情况来分别考虑其预测值与真实值的误差。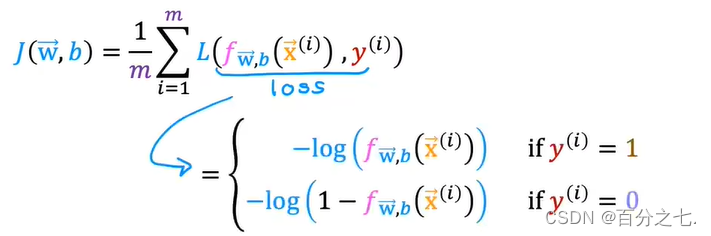
把上述两个公式分别画在二维平面上：


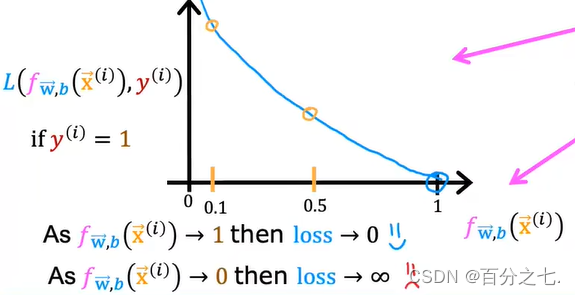
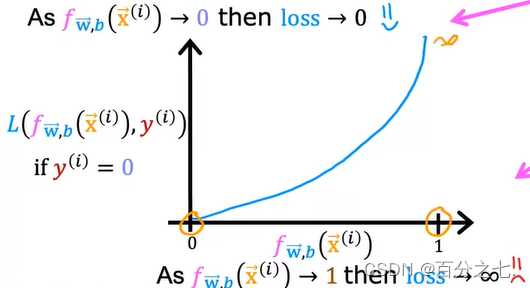
回顾成本的定义，成本是预测值与真实值的差异。当差异越大时，成本越大，模型受到的“惩罚”也就越严重。
成本函数的统一写法：

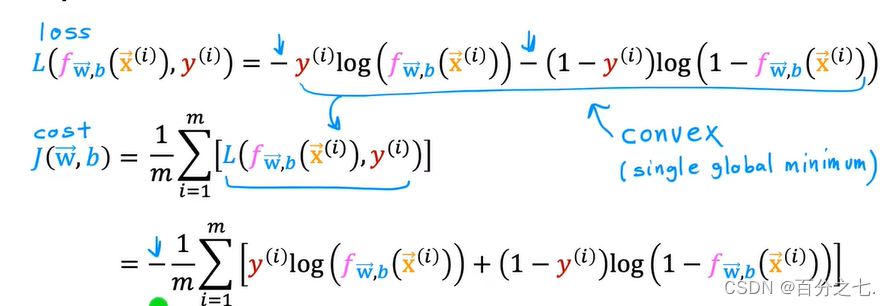
4.梯度下降算法

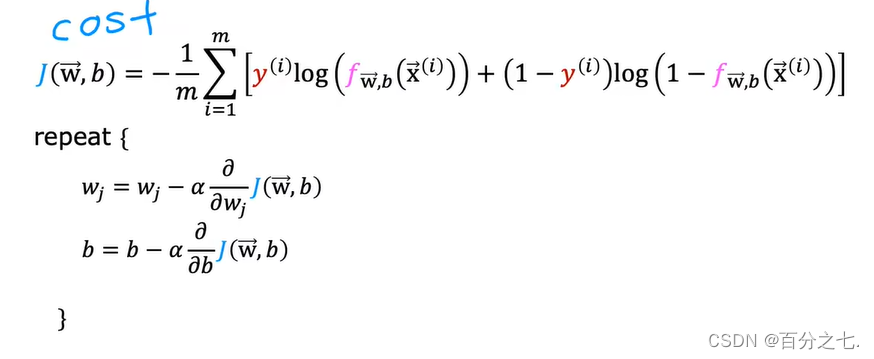
这个公式的形式和线性回归算法的参数迭代公式是一样的。然而预测函数两者的形式完全不同：

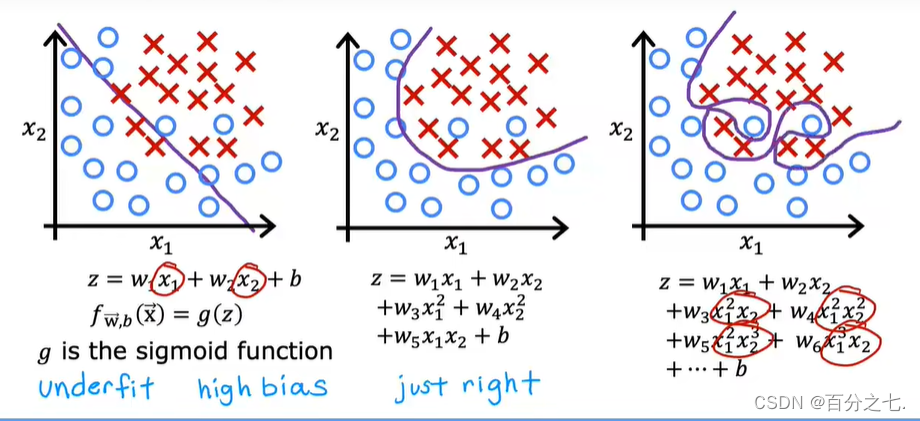
过拟合与欠拟合

过拟合是指模型能很好地拟合训练样本，但对新数据的预测准确性很差。
欠拟合是指模型不能很好地拟合训练样本，且对新数据的预测准确性也不好。
过拟合：

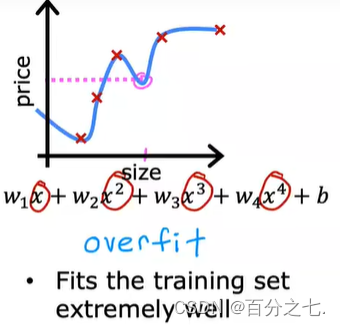
欠拟合：

示例：过拟合是模型非常努力地扭曲自己来找到一个完全符合训练数据的决策边界。

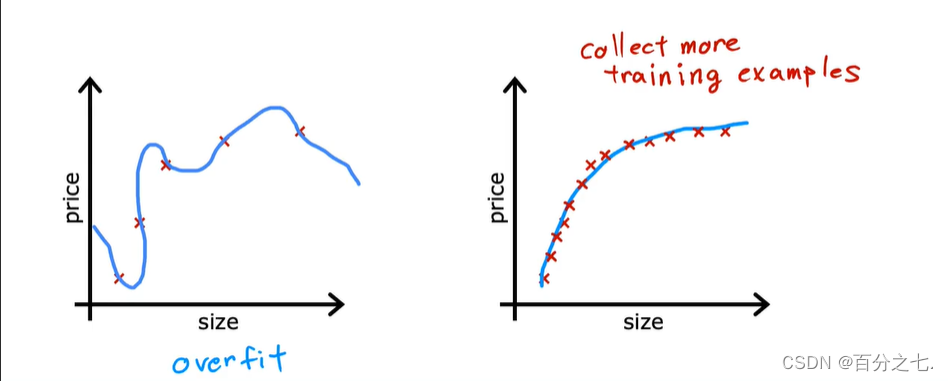
解决过拟合

1.获取更多的训练数据
2.特征选择使用更少的特征
3.正则化来减少父节点的大小

正则化

正则项：
$$\frac{\lambda }{2m}\sum ^n{w}_j^2$$
其中λ是正则化参数。
正则化的成本函数：
$$J(\overrightarrow{\mathrm{w}},b)=\frac{1}{2m}\sum _{i=1}^m{\left(f_{\overrightarrow{\mathrm{w}},b}\left({\overrightarrow{\mathrm{x}}}^{(i)}\right)-y^{(i)}\right)}^2+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$
其中λ的值有两个目的，即要维持对训练样本的拟合，又要避免对训练样本的过拟合。如果λ值等于0，正则项为0，过拟合。如果λ的值非常非常大，则会导致对现有的训练样本出现欠拟合。所以我们想要的是介于两者之间的λ。
从数学角度来看，成本函数增加了一个正则项后，成本函数不再唯一地由预测值与真实值的误差所决定，还和参数w的大小有关。有了这个限制之后，要实现成本函数最小的目的,w就不能随便取值了。比如某个比较大的w值可能会让预测值与真实值的误差值很小，但会导致w^2可很大，最终的结果是成本函数太大。这样，通过调节参数λ就可以控制正则项的权重，从而避免线性回归算法过拟合。

1.线性回归模型正则化

正则化后的参数迭代函数：

其中α和λ是比较小的正数，而m是训练样例的个数，是比较大的正整数。在梯度下降的每一次迭代中，w每次乘以比1略小的数，即收缩一点点，对参数w具有收缩效果。为什么要对w进行收缩昵？因为加入正则项的成本函数和w^2成正比，所以迭代时需要不断地试图减小w的值。

1.逻辑回归模型正则化

使用相同的思路，我们可以对逻辑回归模型的成本函数进行正则化，其方法也是在原来的成本函数基础上加上正则项：
$$J(\overrightarrow{\mathrm{w}},b)=-\frac{1}{m}\sum _{i=1}^m\left[y^{(i)}\log \left(f_{\overrightarrow{\mathrm{w}},b}\left({\overrightarrow{\mathrm{x}}}^{(i)}\right)\right)+\left(1-y^{(i)}\right)\log \left(1-f_{\overrightarrow{\mathrm{w}},b}\left({\overrightarrow{\mathrm{x}}}^{(i)}\right)\right)\right]+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$
相应地，正则化后的参数迭代公式为：

另外需要留意，逻辑回归和线性回归的参数选代算法看起来形式是一样的，但其实它们的算法不一样，因为两个式子的预测函数J不一样。