文章目录
原文章
0. 写在前面
0.1. 通用符号
1️⃣查询有关符号
符号 含义 D D D 待查询的数据集 e e e 带查询的对象, e ∈ D e\in{}D e∈D w 1 , … , w k \mathrm{w}_1, \ldots, \mathrm{w}_k w1,…,wk k k k个给定的关键词, k k k为给定的关键词数量 OUT \text{OUT} OUT 查询结果(输出)的大小 2️⃣ k d - kd\text{-} kd-树有关符号
符号 含义 N N N 叶结点数量 P u P_u Pu 以 k d - kd\text{-} kd-树中间节点 u u u为根的子树的叶节点集,所对应的 R 2 \mathbb{R}^2 R2中的点集 Δ u \Delta_u Δu R 2 \mathbb{R}^2 R2中包住 P u P_u Pu所有点的矩形,矩形长宽平行于坐标 level ( u ) \text{level}(u) level(u) u u u所在的层数,默认根结点在 0 0 0层
- 显然 ∀ u ∈ T \forall{}u\in{}\mathcal{T} ∀u∈T存在 ∣ P u ∣ = O ( N 2 level ( u ) ) \left|P_u\right|=O\left(\cfrac{N}{2^{\text{level } (u)}}\right) ∣Pu∣=O(2level (u)N)
0.2. 通用定义
Item \textbf{Item} Item 定义 查询输入的大小 N : = ∑ e ∈ D ∣ e . Doc ∣ N:=\displaystyle{}\sum_{e \in D} \mid e . \texttt{Doc}\mid N:=e∈D∑∣e.Doc∣即所有对象的文档的总大小 关键词总数 W : = ∣ ⋃ e ∈ D e . Doc ∣ W := \left\lvert \displaystyle\bigcup_{e \in D} e . \texttt{Doc} \right\rvert W:= e∈D⋃e.Doc ,当关键词转化为整数时 [ 1 , W ] [1,W] [1,W]就是关键词集 查询输出集 D ( w 1 , … , w k ) : = D\left(\mathrm{w}_1, \ldots, \mathrm{w}_k\right):= D(w1,…,wk):= 包含所有关键词的对象集 多重对数(符号) polylog ( N ) = log k N \text{polylog}(N) = \log^k N polylog(N)=logkN 0.3. 一些预备知识
1️⃣ L -Norm L\text{-Norm} L-Norm: { p ⃗ = ( p 1 , p 2 , … , p d ) q ⃗ = ( q 1 , q 2 , … , q d ) ⟹ L q ( p , q ) = ( ∑ i = 1 n ∣ p i − q 1 ∣ p ) 1 p \left\{\begin{array}{l}\vec{p}=\left(p_1, p_2, \ldots, p_d\right) \\\\ \vec{q}=\left(q_1, q_2, \ldots, q_d\right)\end{array} \implies \right.L_q(p,q) = \displaystyle\left(\sum_{i=1}^{n} |p_i-q_1|^p \right)^{\frac{1}{p}} ⎩ ⎨ ⎧p=(p1,p2,…,pd)q=(q1,q2,…,qd)⟹Lq(p,q)=(i=1∑n∣pi−q1∣p)p1
- L 1 : L_1\text{: } L1: 即曼哈顿距离,向量的各个分量的绝对值合
- L 2 : L_2\text{: } L2: 即欧几里得距离
- L ∞ : L_{\infty}\text{: } L∞: 即切比雪夫距离, L ∞ ( p , q ) = max i = 1 , … , d ∣ p i − q i ∣ L_{\infty}(p, q)=\max _{i=1, \ldots, d}\left|p_i-q_i\right| L∞(p,q)=maxi=1,…,d∣pi−qi∣
2️⃣线性约束:令 p : = ( p [ 1 ] , … , p [ d ] ) p:=(p[1], \ldots, p[d]) p:=(p[1],…,p[d])则 p p p 受到线性约束 ⇔ ∑ i = 1 d c i ⋅ p [ i ] ≤ c d + 1 \displaystyle\Leftrightarrow \sum_{i=1}^d c_i \cdot p[i] \leq c_{d+1} ⇔i=1∑dci⋅p[i]≤cd+1
3️⃣ k -SI k\text{-SI} k-SI查询概念:给定 m m m个集合 S 1 , S 2 , … , S m S_1, S_2, \ldots, S_m S1,S2,…,Sm
- 查询:给定常数 k ≤ m k\leq{}m k≤m个(整数)关键词 w 1 , w 2 , … , w k \mathrm{w}_1, \mathrm{w}_2, \ldots, \mathrm{w}_k w1,w2,…,wk,返回 ⋂ i = 1 k S w i \displaystyle{}\bigcap_{i=1}^k S_{\mathrm{w}_i} i=1⋂kSwi
- 空查询:返回 ⋂ i = 1 k S w i \displaystyle{}\bigcap_{i=1}^k S_{\mathrm{w}_i} i=1⋂kSwi是否为空
4️⃣ k d - kd\text{-} kd-树
- 定义:给定一个二叉树与点集 P = { x 1 , x 2 , . . . , x N } ⊆ R 2 P=\{x_1,x_2,...,x_N\}\subseteq{}\mathbb{R}^2 P={x1,x2,...,xN}⊆R2
- 对应关系: { 叶结点 i ↔ 一一对应 点 x i 中间结点 u ↔ 一多对应 以 u 为根子树的叶结点 ( P u ) ↔ 一一对应 包住 P u 所有点的矩形 Δ u 根结点 r ↔ 一一对应 所有点 ( P r = P ) \begin{cases} 叶结点i\xleftrightarrow{一一对应}点x_i\\\\ 中间结点u\xleftrightarrow{一多对应}以u为根子树的叶结点(P_u)\xleftrightarrow{一一对应}包住P_u所有点的矩形\Delta_u\\\\ 根结点r\xleftrightarrow{一一对应}所有点(P_{r}=P) \end{cases} ⎩ ⎨ ⎧叶结点i一一对应 点xi中间结点u一多对应 以u为根子树的叶结点(Pu)一一对应 包住Pu所有点的矩形Δu根结点r一一对应 所有点(Pr=P)
- 分割操作:从 u u u开始下降 → { level ( u ) 为偶数 → 将原矩形竖切 level ( u ) 为奇数 → 将原矩形横切 \to{}\begin{cases}\text{level}(u)为偶数\to{}将原矩形竖切\\\\\text{level}(u)为奇数\to{}将原矩形横切\end{cases} →⎩ ⎨ ⎧level(u)为偶数→将原矩形竖切level(u)为奇数→将原矩形横切
- 示例:
1. 研究背景与导论
1.1. 结构化/非结构化查询
1️⃣含义
类型 含义 示例 实现 结构化查询 基于查询对象的预设条件,来检索数据 谓词查询 集合索引(如 kd- \text{kd-} kd-树) 非结构化查询 查询对象不具有任何预设模式 关键词检索 倒排索引 2️⃣示例:以关系
Hotel(price, rating, Doc)为例
- 结构化查询
- 条件 C 1 : \mathbf{C}_1\text{: } C1: 单独约束的结构化条件
SELECT * FROM Hotel WHERE Hotel.price BETWEEN 100 AND 200 AND Hotel.rating >= 8;- 条件 C 1 : \mathbf{C}_1\text{: } C1: 单独约束的结构化条件
SELECT * FROM Hotel WHERE c1 * Hotel.price + c2 * (10 - Hotel.rating) <= c3;- 关键词查询
- 检索得到文档中包含了关键词的对象,关键词例如
pool/parking/bathroom- Ps. \text{Ps. } Ps. 一般会将关键词 Embbeding \text{Embbeding} Embbeding为整数
1.2. 带结构化约束的关键词搜索
1️⃣带关键词的范围查询:对于 D ⊆ R d D \subseteq \mathbb{R}^d D⊆Rd
类型 给定条件 输出集 ORP-KW \text{ORP-KW} ORP-KW d - d\text{-} d-维矩形 q + k q+k q+k个关键词 为点集, e e e在 q q q内 + e +e +e. Doc含所有关键词RR-KW \text{RR-KW} RR-KW d - d\text{-} d-维矩形 q + k q+k q+k个关键词 为矩形集, e q eq eq有交叉 + e +e +e. Doc含所有关键词L ∞ NN-KW L_{\infty}\text{NN-KW} L∞NN-KW 目标点 q + k q+k q+k个关键词 为点集,从 D ( w 1 , … , w k ) D\left(\mathrm{w}_1, \ldots, \mathrm{w}_k\right) D(w1,…,wk)中选择离 q q q最近的 t t t个点 2️⃣带关键词的线性连结:对于 D ⊆ R d D \subseteq \mathbb{R}^d D⊆Rd
类型 给定条件 输出集 LC-KW \text{LC-KW} LC-KW O ( 1 ) O(1) O(1)个线性约束 + k +k +k个关键词 为点集, e e e满足所有约束 + e +e +e. Doc含所有关键词SRP-KW \text{SRP-KW} SRP-KW d - d\text{-} d-维球体 q + k q+k q+k个关键词 为点集, e e e在 q q q内 + e +e +e. Doc含所有关键词L 2 NN-KW L_{2}\text{NN-KW} L2NN-KW 目标点 q + k q+k q+k个关键词 为点集,从 D ( w 1 , … , w k ) D\left(\mathrm{w}_1, \ldots, \mathrm{w}_k\right) D(w1,…,wk)中选离 q q q最近的 t t t个点
- 对于 L 2 NN-KW L_{2}\text{NN-KW} L2NN-KW实际上是 D ⊆ N d D \subseteq \mathbb{N}^d D⊆Nd,且 N ∝ log N \mathbb{N}\propto\log{}N N∝logN
1.3. 研究现状
1.3.1. 面临的困境
1️⃣单独使用结构/关键词查询:需要需要检查大量对象,查询时间渐进等于输入数据量
2️⃣带结构化约束的关键词搜索:在实际数据上表现良好,但理论上缺乏支撑和进展
1.3.2. 本文主要研究
1️⃣设计索引转化框架,将原有仅支持谓词查询的 k d - kd\text{-} kd-树索引,转化为支持关键词的新索引
2️⃣以 OPR-KW \text{OPR-KW} OPR-KW为例,分析得到新索引的复杂度
3️⃣通过将结构化约束的关键词查询,转化为 k-SI \text{k-SI} k-SI查询,从而证明复杂度最优
2. 新索引结果分析
2.1. 复杂性分析: 黄标表示达最优 见 2.2 _{见2.2} 见2.2
查询类型 其它限制 索引空间 查询时间 ORP-KW \text{ORP-KW} ORP-KW d ≤ 2 d \leq 2 d≤2 O ( N ) O(N) O(N) O ( N 1 − 1 k ⋅ ( 1 + OUT 1 k ) ) \small{}O\left(N^{1-\cfrac{1}{k}}\cdot\left(1+\text{OUT}^{\cfrac{1}{k}}\right)\right) O N1−k1⋅ 1+OUTk1 ORP-KW \text{ORP-KW} ORP-KW d ≥ 3 d \geq 3 d≥3 O ( N ⋅ ( log log N ) d − 2 ) \small{}O\left(N \cdot(\log \log N)^{d-2}\right) O(N⋅(loglogN)d−2) O ( N 1 − 1 k ⋅ ( 1 + OUT 1 k ) ) \small{}O\left(N^{1-\cfrac{1}{k}}\cdot\left(1+\text{OUT}^{\cfrac{1}{k}}\right)\right) O N1−k1⋅ 1+OUTk1 RR-KW \text{RR-KW} RR-KW$ N/A \text{N/A} N/A O ( N ⋅ ( log log N ) 2 d − 2 ) \small{}O\left(N \cdot(\log \log N)^{2d-2}\right) O(N⋅(loglogN)2d−2) O ( N 1 − 1 k ⋅ ( 1 + OUT 1 k ) ) \small{}O\left(N^{1-\cfrac{1}{k}}\cdot\left(1+\text{OUT}^{\cfrac{1}{k}}\right)\right) O N1−k1⋅ 1+OUTk1 L ∞ NN-KW L_{\infin}\text{NN-KW} L∞NN-KW N/A \text{N/A} N/A O ( N ⋅ ( log log N ) 2 d − 2 ) \small{}O\left(N \cdot(\log \log N)^{2d-2}\right) O(N⋅(loglogN)2d−2) O ( N 1 − 1 k ⋅ t 1 k ⋅ log N ) \small{}O\left(N^{1-\cfrac{1}{k}}\cdot{}t^{\cfrac{1}{k}}\cdot\log{}N\right) O N1−k1⋅tk1⋅logN LC-KW \text{LC-KW} LC-KW$ d ≤ k d\leq{}k d≤k O ( N ) O(N) O(N) O ( N 1 − 1 k ⋅ ( log N + OUT 1 k ) ) \small{}O\left(N^{1-\cfrac{1}{k}}\cdot\left(\log{}N+\text{OUT}^{\cfrac{1}{k}}\right)\right) O N1−k1⋅ logN+OUTk1 LC-KW \text{LC-KW} LC-KW d > k d>k d>k O ( N ) O(N) O(N) O ( N 1 − 1 d + N 1 − 1 k ⋅ OUT 1 k ) \small{}O\left(N^{1-\cfrac{1}{d}}+N^{1-\cfrac{1}{k}}\cdot\text{OUT}^{\cfrac{1}{k}}\right) O N1−d1+N1−k1⋅OUTk1 SRP-KW \text{SRP-KW} SRP-KW d ≤ k − 1 d\leq{}k-1 d≤k−1 O ( N ) O(N) O(N) O ( N 1 − 1 k ⋅ ( log N + OUT 1 k ) ) \small{}O\left(N^{1-\cfrac{1}{k}}\cdot\left(\log{}N+\text{OUT}^{\cfrac{1}{k}}\right)\right) O N1−k1⋅ logN+OUTk1 SRP-KW \text{SRP-KW} SRP-KW d > k − 1 d>k-1 d>k−1 O ( N ) O(N) O(N) O ( N 1 − 1 d + N 1 − 1 k ⋅ OUT 1 k ) \small{}O\left(N^{1-\cfrac{1}{d}}+N^{1-\cfrac{1}{k}}\cdot\text{OUT}^{\cfrac{1}{k}}\right) O N1−d1+N1−k1⋅OUTk1 L 2 NN-KW L_2\text{ NN-KW} L2 NN-KW d ≤ k − 1 d\leq{}k-1 d≤k−1 O ( N ) O(N) O(N) O ( log N ⋅ N 1 − 1 k ⋅ ( log N + OUT 1 k ) ) \small{}O\left(\log{}N\cdot{}N^{1-\cfrac{1}{k}}\cdot\left(\log{}N+\text{OUT}^{\cfrac{1}{k}}\right)\right) O logN⋅N1−k1⋅ logN+OUTk1 L 2 NN-KW L_2\text{ NN-KW} L2 NN-KW d > k − 1 d>k-1 d>k−1 O ( N ) O(N) O(N) O ( N 1 − 1 d + 1 + N 1 − 1 k ⋅ t 1 k ) \small{}O\left(N^{1-\cfrac{1}{d+1}}+N^{1-\cfrac{1}{k}}\cdot{}t^{\cfrac{1}{k}}\right) O N1−d+11+N1−k1⋅tk1 2.2. 紧致性讨论: O ( N 1 − 1 k ⋅ ( 1 + OUT 1 k ) ) \tiny{}O\left(N^{1-\cfrac{1}{k}}\cdot\left(1+\text{OUT}^{\cfrac{1}{k}}\right)\right) O(N1−k1⋅(1+OUTk1))最优
2.2.1. k -SI k\text{-SI} k-SI查询的等价: 将原问题分析转化为对 k -SI k\text{-SI} k-SI的分析
1️⃣ k -SI k\text{-SI} k-SI查询 ↔ 等价 \xleftrightarrow{等价} 等价 纯粹关键词查询
- D ( w 1 , … , w k ) ⇒ ⋂ i = 1 k S w i \displaystyle{}D\left(\mathrm{w}_1, \ldots, \mathrm{w}_k\right)\xRightarrow{}\bigcap_{i=1}^k S_{\mathrm{w}_i} D(w1,…,wk)i=1⋂kSwi:令集合 S w i S_{\mathrm{w}_i} Swi收集所有包含了 w i \mathrm{w}_i wi关键词的对象 e e e (倒排索引)
- D ( w 1 , … , w k ) ⇐ ⋂ i = 1 k S w i \displaystyle{}\displaystyle{}D\left(\mathrm{w}_1, \ldots, \mathrm{w}_k\right)\xLeftarrow{}\bigcap_{i=1}^k S_{\mathrm{w}_i} D(w1,…,wk)i=1⋂kSwi:为每个对象 e ∈ D = ⋃ i = 1 m S i e\in{}\displaystyle{}D=\bigcup_{i=1}^m S_i e∈D=i=1⋃mSi创建关键词 e . e. e.
Doc: = { i ∣ e ∈ S i } :=\left\{i \mid e \in S_i\right\} :={i∣e∈Si}
- 例如: S 1 S 3 S_1S_3 S1S3包含 e e e则 e . e. e.
Doc={1,3} \text{=\{1,3\}} ={1,3},将同时拥有这些关键词转化为同时在这些集合中2️⃣ k -SI k\text{-SI} k-SI查询 ↔ 等价 \xleftrightarrow{等价} 等价 结构化限制的关键词查询:
- 以搜索矩形 q ∈ R d q\in{}\mathbb{R}^d q∈Rd的 ORP-KW \text{ORP-KW} ORP-KW为例:只需要基于之前的操作,将 e ∈ D e\in{}D e∈D映射到 R d \mathbb{R}^d Rd任一点即可
- 类似可得: ORP-KW/RR-KW/LC-KW \text{ORP-KW/RR-KW/LC-KW} ORP-KW/RR-KW/LC-KW本质上都是 k -SI k\text{-SI} k-SI查询的泛化
2.2.2. k -SI k\text{-SI} k-SI查询紧致性分析基础
1️⃣ k -SI k\text{-SI} k-SI被广泛验证的两个猜想:对于 N : = ∑ i = 1 m ∣ S i ∣ \displaystyle{}N:=\sum_{i=1}^m\left|S_i\right| N:=i=1∑m∣Si∣有
猜想 δ \delta δ 给定查询时间 必须使用的索引空间大小 强相交 δ ∈ ( 0 , 1 ] \delta \in(0,1] δ∈(0,1] O ( N 1 − δ + OUT ) O\left(N^{1-\delta}+\text{OUT}\right) O(N1−δ+OUT) Ω ( N 1 + δ polylog N ) \Omega\left(\cfrac{N^{1+\delta}}{\text{polylog }N}\right) Ω(polylog NN1+δ) 强 k k k不相交 δ ∈ ( 0 , 1 − 1 k ] \delta \in(0,1-\cfrac{1}{k}] δ∈(0,1−k1] O ( N 1 − 1 k − δ ) O\left(N^{1-\cfrac{1}{k}-\delta}\right) O N1−k1−δ Ω ( N 1 + k δ polylog N ) \Omega\left(\cfrac{N^{1+k\delta}}{\text{polylog }N}\right) Ω(polylog NN1+kδ) 2️⃣引理:如果索引结构 1 1 1存在,则索引结构 2 2 2也必定成立
索引 索引空间 查询时间 1 1 1 O ( N ⋅ polylog N ) O\left(N\cdot\text{polylog }N\right) O(N⋅polylog N) O ( N 1 − 1 k + N 1 − 1 k ⋅ OUT 1 k − ϵ + O U T ) O\left(N^{1-\cfrac{1}{k}}+N^{1-\cfrac{1}{k}} \cdot \text { OUT }^{\cfrac{1}{k}-\epsilon}+\mathrm{OUT}\right) O N1−k1+N1−k1⋅ OUT k1−ϵ+OUT 2 2 2 O ( N ⋅ polylog N ) O\left(N\cdot\text{polylog }N\right) O(N⋅polylog N) O ( N 1 − min { 1 k , ϵ 1 − 1 k + ϵ } + O U T ) O\left(N^{1-\min \left\{\cfrac{1}{k}, \cfrac{\epsilon}{1-\frac{1}{k}+\epsilon}\right\}}+\mathrm{OUT}\right) O N1−min{k1,1−k1+ϵϵ}+OUT 2.2.3. 多项式紧致性分析
🤔先说结论: k -SI k\text{-SI} k-SI查询满足以下性质
- 给定索引空间 O ( N ⋅ polylog N ) ⟹ 最优查询时间为 O ( N 1 − 1 k ( 1 + OUT 1 k ) + OUT ) 给定索引空间O\left(N\cdot\text{polylog }N\right)\implies最优查询时间为O\left(N^{1-\cfrac{1}{k}}\left(1+\text { OUT }^{\cfrac{1}{k}}\right)+\text{OUT}\right) 给定索引空间O(N⋅polylog N)⟹最优查询时间为O N1−k1 1+ OUT k1 +OUT
- Ps. \text{Ps. } Ps.
- 展开后的三项多项式都达到了最优 展开后的三项多项式都达到了最优 展开后的三项多项式都达到了最优
- 显而易见有 lim k → ∞ O ( N 1 − 1 k ( 1 + OUT 1 k ) + OUT ) = O ( N + OUT ) \text{显而易见有}\displaystyle\lim_{k \to \infty} O\left(N^{1-\cfrac{1}{k}}\left(1+\text{OUT}^{\cfrac{1}{k}}\right) + \text{OUT}\right) = O(N + \text{OUT}) 显而易见有k→∞limO N1−k1 1+OUTk1 +OUT =O(N+OUT)
1️⃣ O ( N 1 − 1 k ) O\left(N^{1-\cfrac{1}{k}}\right) O N1−k1 为最优证明:
- 假设存在更优解 O ( N 1 − 1 k − ϵ + N 1 − 1 k ⋅ OUT 1 k + OUT ) O\left(N^{1-\cfrac{1}{k}-\epsilon}+N^{1-\cfrac{1}{k}}\cdot\text { OUT }^{\cfrac{1}{k}}+\text{OUT}\right) O N1−k1−ϵ+N1−k1⋅ OUT k1+OUT
- 整个 k -SI k\text{-SI} k-SI查询在 OUT \text{OUT} OUT为空时最快,达到 O ( N 1 − 1 k − ϵ ) O\left(N^{1-\cfrac{1}{k}-\epsilon}\right) O N1−k1−ϵ
- 这就是 k -SI k\text{-SI} k-SI空查询的时间,等于这个时间返回 1 1 1,超出这个时间则立即终止并返回 0 0 0
- 根据强 k k k不相交猜想,索引空间为 Ω ( N 1 + k δ polylog N ) \Omega\left(\cfrac{N^{1+k\delta}}{\text{polylog }N}\right) Ω(polylog NN1+kδ)与 O ( N ⋅ polylog N ) O\left(N\cdot\text{polylog }N\right) O(N⋅polylog N)冲突,所以已最优
2️⃣ O ( N 1 − 1 k ) ⋅ OUT 1 k O\left(N^{1-\cfrac{1}{k}}\right)\cdot\text { OUT }^{\cfrac{1}{k}} O N1−k1 ⋅ OUT k1为最优证明:
- 对于 δ = min { 1 k , ϵ 1 − 1 k + ϵ } \delta=\min \left\{\cfrac{1}{k}, \cfrac{\epsilon}{1-\frac{1}{k}+\epsilon}\right\} δ=min{k1,1−k1+ϵϵ},考虑引理中的两个索引
- 如果索引 1 1 1存在 → 引理 \xrightarrow{引理} 引理索引 2 2 2存在 { → 强相交猜想 索引空间至少为 Ω ( N 1 + δ polylog N ) 索引空间为 O ( N ⋅ polylog N ) → 上下不符 矛盾 \begin{cases}\xrightarrow{强相交猜想}索引空间至少为\Omega\left(\cfrac{N^{1+\delta{}}}{\text{polylog }N}\right)\\\\索引空间为O\left(N\cdot\text{polylog }N\right)\end{cases}\xrightarrow{上下不符}矛盾 ⎩ ⎨ ⎧强相交猜想索引空间至少为Ω(polylog NN1+δ)索引空间为O(N⋅polylog N)上下不符矛盾
- 所以索引 1 1 1不存在,即不可能优化到索引 1 1 1中所示的查询时间
3️⃣ O ( OUT ) O\left(\text{OUT}\right) O(OUT)最优:因为输出不可避免
3. 索引转换框架
3.0. Intro
🤔要干啥:原始 k d - kd\text{-} kd-树: 纯集合索引 → 索引转换框架 \xrightarrow{索引转换框架} 索引转换框架调整 k d - kd\text{-} kd-树: 支持关键词查询 (此处以 ORP-KW \text{ORP-KW} ORP-KW为例)
🚀聚焦的问题: ORP-KW \text{ORP-KW} ORP-KW的时间复杂度为 O ( N 1 − 1 k ⋅ ( 1 + OUT 1 k ) ) O\left(N^{1-\cfrac{1}{k}}\cdot\left(1+\text{OUT}^{\cfrac{1}{k}}\right)\right) O N1−k1⋅ 1+OUTk1
3.1. 数据结构
0️⃣一般位置假设:所有对象 e ∈ D ⊆ R 2 e\in{}D\subseteq{}\mathbb{R}^2 e∈D⊆R2无共享的 x y xy xy坐标,以下分析都基于这个假设
1️⃣在 D D D的详细集上构建 k d - kd\text{-} kd-树 T \mathcal{T} T:对于 e ∈ D e\in{}D e∈D通过以下规则构建详细集 p ∈ P p\in{}P p∈P
原集合 D D D 详细集 P P P 单个 e 1 ∈ D e_1\in{}D e1∈D ∣ e 1 . \mid{}e_1. ∣e1. Doc∣ \mid{} ∣个 e 1 ∈ P e_1\in{}P e1∈P单个 e 2 ∈ D e_2\in{}D e2∈D ∣ e 2 . \mid{}e_2. ∣e2. Doc∣ \mid{} ∣个 e 2 ∈ P e_2\in{}P e2∈P… … 2️⃣定义结点 u u u的活动/枢纽集
- 定义:考虑在 k d - kd\text{-} kd-树的 u u u结点发生以下分割

- u u u的活动集 D u a c t D_u^{act} Duact: { D u a c t ⇔ Δ u D v 1 a c t / D v 2 a c t ⇔ Δ v 1 / Δ v 2 \begin{cases}D_u^{act}\xLeftrightarrow{}\Delta_{u}\\\\D_{v_1}^{act}/D_{v_2}^{act}\xLeftrightarrow{}\Delta_{v_1}/\Delta_{v_2}\end{cases} ⎩ ⎨ ⎧Duact ΔuDv1act/Dv2act Δv1/Δv2
- u u u的枢纽集 D u p v t D_u^{pvt} Dupvt: Δ v 1 \Delta_{v_1} Δv1或 Δ v 2 \Delta_{v_2} Δv2边界上对象的集合
- 性质: D u p v t ⊆ D u a c t ⊆ D D_u^{pvt} \subseteq D_u^{act} \subseteq D Dupvt⊆Duact⊆D, ∣ D u p v t ∣ = O ( 1 ) |D_u^{pvt}|=O(1) ∣Dupvt∣=O(1)
3️⃣定义结点 u u u的大小关键字
- 定义:如果关键字 w \mathrm{w} w在 u u u处满足 ∣ D u a c t ( w ) ∣ ≥ N u 1 − 1 k \left|D_u^{a c t}(\mathrm{w})\right| \geq N_u^{1-\frac{1}{k}} ∣Duact(w)∣≥Nu1−k1则 w \mathrm{w} w为 u u u大关键字,反之为小关键字
- D u a c t ( w ) : = { e ∈ D u a c t ∣ w ∈ e . DOC } D_u^{act}(\mathrm{w}) := \left\{ e \in D_u^{act} \mid \mathrm{w} \in e . \verb|DOC| \right\} Duact(w):={e∈Duact∣w∈e.DOC}即 u u u活动集中包含 w \mathrm{w} w关键字的对象集
- N u : = ∑ e ∈ D u a c t ∣ e . DOC ∣ N_u := \displaystyle\sum_{e \in D_u^{act}} |e . \verb|DOC|| Nu:=e∈Duact∑∣e.DOC∣即 u u u活动集中每个对象关键词数量总,显然 N u ≤ ∣ P u ∣ = O ( N 2 level ( u ) ) N_u \leq\left|P_u\right|=O\left(\cfrac{N}{2^{\text {level }(u)}}\right) Nu≤∣Pu∣=O(2level (u)N)
- 性质: u u u处最多只能有 N u 1 k N_u^{\frac{1}{k}} Nuk1个大关键字
4️⃣定义结点 u u u的复数附属结构 T u T_u Tu
- T u T_u Tu功能
T u T_u Tu输入 T u T_u Tu输出 适用 结点 u u u 枢纽集 D u p v t D_u^{pvt} Dupvt 中间 + + +叶结点 结点 u u u,关键字 w \mathrm{w} w w \mathrm{w} w在 u u u是否为大关键字 中间结点 结点 u u u, u u u处 k k k个大关键字 w 1 , … , w k \mathrm{w}_1, \ldots, \mathrm{w}_k w1,…,wk, u u u子节点 v v v ⋂ i = 1 k D v a c t ( w i ) \displaystyle{}\bigcap_{i=1}^k D_v^{act}\left(\mathrm{w}_i\right) i=1⋂kDvact(wi)是否为空 中间结点 - T u T_u Tu执行时间: O ( N u 1 k ) word + O ( N u ) bit O(N_u^{\frac{1}{k}})\text{ word}+O(N_u)\text{ bit} O(Nuk1) word+O(Nu) bit
5️⃣数据结构的物化
- 含义:数据结构从概念模型 → \to →内存实体
- D u a c t ( w ) D_u^{act}(\mathrm{w}) Duact(w)物化的条件: w \mathrm{w} w是 u u u处的小关键字 + + + w \mathrm{w} w在 u u u的所有祖先处为大关键字
3.2. 转换算法: 以 ORP-KW \text{ORP-KW} ORP-KW查询为例
1️⃣算法的一些模块化操作:给定矩形 q q q和关 W = { w 1 , … , w k } \mathbb{W}=\{\mathrm{w}_1, \ldots, \mathrm{w}_k\} W={w1,…,wk}键词
- 访问结点 u u u操作
- 读取 ∀ e ∈ D u p v t \forall{}e\in{}D_u^{pvt} ∀e∈Dupvt
- 如果 e e e被 q q q覆盖 + e . +e. +e.
Doc包含所有关键词,则报告 e e e- 下降判断操作:要求以下两个操作同时返回是,才访问 u u u的子节点 v v v
- u + 关键字集 W → T u { W 在 u 都为大关键字 + 子节点 v → T u { ⋂ i = 1 k D v a c t ( w i ) 空 → 否 ⋂ i = 1 k D v a c t ( w i ) 不空 → 是 W 在 u 存在小关键字 → 否 u+关键字集\mathbb{W}\xrightarrow{T_u}\begin{cases}\mathbb{W}在u都为大关键字+子节点v\xrightarrow{T_u}\begin{cases}\displaystyle{}\bigcap_{i=1}^k D_v^{act}\left(\mathrm{w}_i\right)空\to{否}\\\\\displaystyle{}\bigcap_{i=1}^k D_v^{act}\left(\mathrm{w}_i\right)不空\to{是}\end{cases}\\\\\mathbb{W}在u存在小关键字\to{}否\end{cases} u+关键字集WTu⎩ ⎨ ⎧W在u都为大关键字+子节点vTu⎩ ⎨ ⎧i=1⋂kDvact(wi)空→否i=1⋂kDvact(wi)不空→是W在u存在小关键字→否
- 矩形 q q q与子节点对应矩形 Δ v \Delta_v Δv有交叉 → \to{} →是
- 停止下降后的报告操作:假设 u u u处含有小关键字 w i \mathrm{w}_i wi从而导致下降终止
- 物化 D u a c t ( w i ) D_u^{act}\left(\mathrm{w}_i\right) Duact(wi) ( u u u的活动集中包括了 w i \mathrm{w}_i wi关键词的对象)
- 检查所有 e ∈ D u a c t ( w i ) e\in{}D_u^{act}\left(\mathrm{w}_i\right) e∈Duact(wi),如果 e e e被 q q q覆盖 + e . +e. +e.
Doc包含所有关键词,则报告 e e e2️⃣算法结构
- 算法流程
- 算法最终输出: q ∩ D ( w 1 , … , w k ) q \cap D\left(\mathrm{w}_1, \ldots, \mathrm{w}_k\right) q∩D(w1,…,wk)
3.3. 算法分析:交叉敏感性的界定
1️⃣辅助数据结构
- 查询子树 T qry \mathcal{T}_{\text {qry}} Tqry:对 T \mathcal{T}_{\text {}} T执行查询过程中遍历的点,所得到的子树
- 交叉子树 T cross \mathcal{T}_{\text {cross}} Tcross: T qry \mathcal{T}_{\text {qry}} Tqry中交叉结点构成的子树
- 覆盖结点: T qry \mathcal{T}_{\text {qry}} Tqry中,满足对应矩形 Δ u ⊆ \Delta_{}u\subseteq Δu⊆查询矩形 q q q的结点 u u u
- 交叉结点: T qry \mathcal{T}_{\text {qry}} Tqry中其它
2️⃣复杂度分析
算法所处理的结构 时间复杂度 T qry \mathcal{T}_{\text {qry}} Tqry中间结点 O ( 1 ) O(1) O(1) T qry \mathcal{T}_{\text {qry}} Tqry叶节点 O ( N z 1 − 1 k ) O\left(N_z^{1-\frac{1}{k}}\right) O(Nz1−k1) 覆盖结点总耗时 O ( N 1 − 1 k ( 1 + O U T 1 k ) ) O\left(N^{1-\cfrac{1}{k}}\left(1+\mathrm{OUT}^{\cfrac{1}{k}}\right)\right) O N1−k1 1+OUTk1 交叉结点总耗时 ∑ int u of T cross O ( 1 ) + ∑ leaf z of T cross O ( N z 1 − 1 k ) \displaystyle{}\sum_{\text {int } u \text { of } \mathcal{T}_{\text {cross }}} O(1)+\sum_{\text {leaf } z \text { of } \mathcal{T}_{\text {cross }}} O\left(N_z^{1-\frac{1}{k}}\right) int u of Tcross ∑O(1)+leaf z of Tcross ∑O(Nz1−k1)
- 总体复杂度 = = =覆盖节点耗时 + + +交叉节点耗时
- 对大多数索引来说,覆盖结点总耗时都不变,形成差异化的是交叉结点耗时,故定义为交叉敏感性
3️⃣交叉敏感性的界定
- 对任意二维矩形查询区域 q q q,交叉敏感性为 O ( N 1 − 1 k ) O\left(N^{1-\frac{1}{k}}\right) O(N1−k1)
- 由此可得 ORP-KW \text{ORP-KW} ORP-KW查询的总耗时就是 O ( N 1 − 1 k ( 1 + O U T 1 k ) ) O\left(N^{1-\cfrac{1}{k}}\left(1+\mathrm{OUT}^{\cfrac{1}{k}}\right)\right) O N1−k1 1+OUTk1
- 证明思路:
- 处理特殊情况: q q q为垂线时交叉敏感性为 O ( N 1 − 1 k ) O\left(N^{1-\frac{1}{k}}\right) O(N1−k1)
- 处理一般情况:
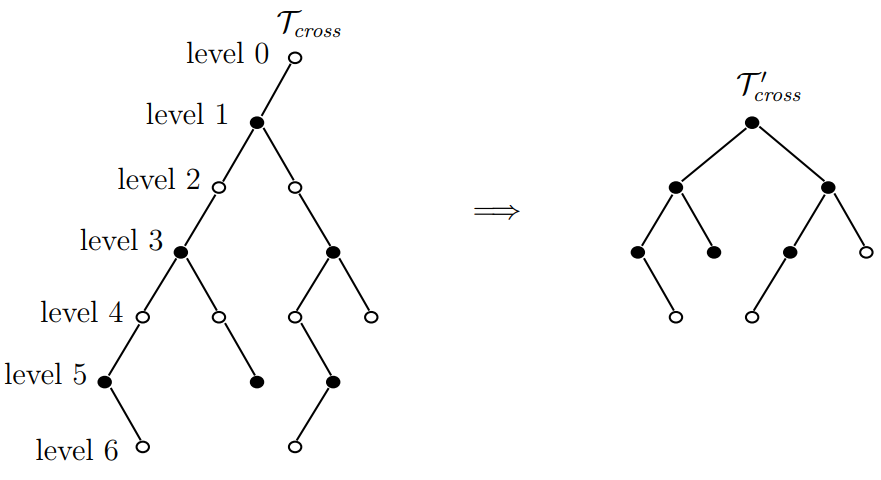
- k d - kd\text{-} kd-树压缩: k d - kd\text{-} kd-树每偶数层仅一点在 T cross \mathcal{T}_{\text {cross}} Tcross中 → \to{} →删除(非叶)偶数层让上下的奇数层直连
- 对简化的树结构分析可得,交叉敏感性任然是 O ( N 1 − 1 k ) O\left(N^{1-\frac{1}{k}}\right) O(N1−k1)
4. 一种关键词下的降维技术
4.0. Intro
🚀聚焦的问题:用一种降维技术,使每二维以后增加一个维度, ORP-KW \text{ORP-KW} ORP-KW空间复杂度只加 O ( log 2 N ) O(\log^2 N) O(log2N)
🌵分析的基础:关于 ORP-KW \text{ORP-KW} ORP-KW索引的一个引理,如果索引 1 1 1存在,则索引 2 2 2也一定存在
索引 维度限制 索引空间 查询时间 ORP-KW \text{ORP-KW} ORP-KW(索引 1 1 1) d = λ ≥ 2 d=\lambda{}\geq{}2 d=λ≥2 O ( N ⋅ ( log log N ) λ − 2 ) O\left(N \cdot(\log \log N)^{\lambda-2}\right) O(N⋅(loglogN)λ−2) ( N 1 − 1 k ⋅ ( 1 + OUT 1 k ) ) \left(N^{1-\cfrac{1}{k}}\cdot\left(1+\text{OUT}^{\cfrac{1}{k}}\right)\right) N1−k1⋅ 1+OUTk1 ORP-KW \text{ORP-KW} ORP-KW(索引 2 2 2) d = λ + 1 d=\lambda{}+1 d=λ+1 O ( N ⋅ ( log log N ) λ − 1 ) O\left(N \cdot(\log \log N)^{\lambda-1}\right) O(N⋅(loglogN)λ−1) ( N 1 − 1 k ⋅ ( 1 + OUT 1 k ) ) \left(N^{1-\cfrac{1}{k}}\cdot\left(1+\text{OUT}^{\cfrac{1}{k}}\right)\right) N1−k1⋅ 1+OUTk1
- Ps. \text{Ps. } Ps. 对于 D ⊂ R λ + 1 D\subset{}\mathbb{R}^{\lambda{}+1} D⊂Rλ+1称第一维度为 x x x维
🤔分析思路:上述引理 + + +二维时 ORP-KW \text{ORP-KW} ORP-KW的复杂度分析 → \to →高纬时 ORP-KW \text{ORP-KW} ORP-KW的复杂度
4.1. 数据结构
1️⃣基础的一些定义
- 子集权重: weight ( D ′ ) : = ∑ e ∈ D ′ ⊆ D ∣ e . DOC ∣ \displaystyle{}\text {weight }\left(D^{\prime}\right):=\sum_{e \in D^{\prime}\subseteq D} \mid e . \verb|DOC| \mid weight (D′):=e∈D′⊆D∑∣e.DOC∣,显然有 weight ( D ′ ) ≥ ∣ D ′ ∣ \text{weight}\left(D^{\prime}\right) \geq\left|D^{\prime}\right| weight(D′)≥∣D′∣
- D ′ D^{\prime} D′的 f - f\text{-} f-平衡分割:无论 D ′ D^{\prime} D′和 f f f如何,总有一元组 ( D 1 , D 2 , … , D f , e 1 ∗ , e 2 ∗ , … , e f − 1 ∗ ) \left(D_1, D_2, \ldots, D_f, e_1^*, e_2^*, \ldots, e_{f-1}^*\right) (D1,D2,…,Df,e1∗,e2∗,…,ef−1∗)满足
- D i ⊆ D D_i\subseteq{}D Di⊆D, e i ∈ D ′ e_i\in{}D^{\prime} ei∈D′或者 e i = null e_i=\text{null} ei=null
- D 1 , D 2 , … , D f , { e 1 ∗ } , { e 2 ∗ } , … , { e f − 1 ∗ } D_1, D_2, \ldots, D_f,\left\{e_1^*\right\},\left\{e_2^*\right\}, \ldots,\left\{e_{f-1}^*\right\} D1,D2,…,Df,{e1∗},{e2∗},…,{ef−1∗}彼此互斥,并且并集为 D ′ D^{\prime} D′
- D i D_i Di中每个对象的 x x x坐标,都小于 D i + k D_{i+k} Di+k中每个对象的 x x x坐标
- weight ( D i ) ≤ weight ( D i ) f \text{weight}\left(D_{i}\right) \leq\cfrac{\text{weight}\left(D_{i}\right)}{f} weight(Di)≤fweight(Di)
2️⃣定义树 T \mathcal{T} T的活动/枢纽集
- u ∈ T u\in{\mathcal{T}} u∈T中活动集 D u a c t D_u^{act} Duact:与先前定义一样与 Δ u \Delta_{u} Δu对应
- u ∈ T u\in{\mathcal{T}} u∈T中枢纽集 D u p v t D_u^{pvt} Dupvt:对 D u D_u Du,执行 f u : = 2 ⋅ 2 k level ( u ) − f_u:=2 \cdot 2^{k^{\text{level}(u)}}- fu:=2⋅2klevel(u)−平衡切割 ( D 1 , … , D f u , e 1 ∗ , … , e f u − 1 ∗ ) \left(D_1, \ldots, D_{f_u}, e_1^*, \ldots, e_{f_u-1}^*\right) (D1,…,Dfu,e1∗,…,efu−1∗)

- 对于 u u u本身: D u p v t : = { e 1 ∗ , … , e f u − 1 ∗ } D_u^{pvt}:=\left\{e_1^*, \ldots, e_{f_u-1}^*\right\} Dupvt:={e1∗,…,efu−1∗}
- 生成 u u u的(多)子节点 v → { D 1 , … , D f u 皆空 → u 为叶结点 ( v 不存在 ) 否则 → 为每个非空 D i 创建子节点 → D v a c t : = D i {}v\to{}\begin{cases}D_1, \ldots, D_{f_u}皆空\to{}u为叶结点(v不存在)\\\\否则\to{}为每个非空D_i创建子节点\to{}D_v^{act}:=D_i\end{cases} v→⎩ ⎨ ⎧D1,…,Dfu皆空→u为叶结点(v不存在)否则→为每个非空Di创建子节点→Dvact:=Di
3️⃣定义树结点 u u u的次级结构:考虑 input → T u output \text{input}\xrightarrow{T_u}\text{output} inputTuoutput
- input \text{input} input:所在结点 u + k u+k u+k个关键词 + ( λ +1 ) - +(\lambda\text{+1})\text{-} +(λ+1)-矩形 q q q
- 且 q q q在 x x x的投影为 ( − ∞ , ∞ ) (-\infty, \infty) (−∞,∞)
- output \text{output} output: u u u活动集中的部分对象 e e e,满足 e e e被矩形 q q q覆盖 + + + e . e. e.
Doc包含所有关键词4.2. 查询算法
1️⃣一些记号
- σ ( u ) \sigma(u) σ(u)为覆盖 D u a c t D_u^{act} Duact中所有点的 x x x坐标的最紧密区间
- q [ i ] q[i] q[i]为 q q q在 i ∈ [ 1 , λ + 1 ] i \in[1, \lambda+1] i∈[1,λ+1]上的投影区间, q [ 1 ] q[1] q[1]是 x x x维的区间
2️⃣查询操作:输入 ( λ + 1 ) - (\lambda+1)\text{-} (λ+1)-矩形 q q q,关键词 w 1 , … , w k \mathrm{w}_1, \ldots, \mathrm{w}_k w1,…,wk
- 访问满足以下条件的结点 u ∈ T u\in{}\mathcal{T} u∈T,并将被访问到的结点剥离出为 T qry \mathcal{T}_{\text {qry}} Tqry
- σ ( u ) ∩ q [ 1 ] ≠ ∅ \sigma(u) \cap q[1] \neq \emptyset σ(u)∩q[1]=∅
- u u u的所有祖先 v v v的 σ ( v ) \sigma(v) σ(v),都没完全包含在 q [ 1 ] q[1] q[1]中
- 将 T qry \mathcal{T}_{\text {qry}} Tqry中的点分类
- 类型 1 1 1(图中黑点): σ ( u ) ⊆ q [ 1 ] \sigma{(u)}\subseteq{}q[1] σ(u)⊆q[1]
- 类型 2 2 2(图中白点):其它结点,每层最多只有两个白点
- 报告对象
- 对类型 1 1 1的点:执行 T u T_u Tu以报告对象
- 对类型 2 2 2的点:检查并报告枢纽集中合要求的对象,时间开销 O ( ∣ D u p v t ∣ ) = O ( f u ) O\left(\left|D_u^{pvt}\right|\right)=O\left(f_u\right) O(∣Dupvt∣)=O(fu)
4.3. 复杂度分析
1️⃣空间复杂度分析
- T \mathcal{T} T每层结点的辅助结构总占用空间 O ( N ⋅ ( log log N ) λ − 2 ) O\left(N \cdot(\log \log N)^{\lambda-2}\right) O(N⋅(loglogN)λ−2)
- 由于 T \mathcal{T} T有 O ( log log N ) O(\log \log N) O(loglogN)层故总空间为 O ( N ⋅ ( log log N ) λ − 1 ) O\left(N \cdot(\log \log N)^{\lambda-1}\right) O(N⋅(loglogN)λ−1)
2️⃣时间复杂度分析
- 类型 1 1 1结点成本: O ( N 1 − 1 k ) O\left(N^{1-\frac{1}{k}}\right) O(N1−k1)
- 类型 2 2 2结点成本: O ( N 1 − 1 k ) O\left(N^{1-\frac{1}{k}}\right) O(N1−k1)
























 1498
1498

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








