STB仿真和AC仿真的区别与联系

烟波蓑衣

已于 2024-10-12 19:34:43 修改

阅读量3.8k

点赞数 44

文章标签：笔记其他

于 2024-10-12 16:12:25 首次发布

本文链接：https://blog.csdn.net/qq_65548634/article/details/142875698

版权

我们之所以想讨论stb和ac仿真的区别是因为我们在仿真稳定性时遇到了问题，其中ac仿真通过给定1V的激励源然后开环仿真可以得到波特图，然后由波特图得到相位裕度；而通过stb仿真也能得到相位裕度但是两者之间存在区别，这两个不知道哪一个是准确的，所以现在的问题是相位裕度是和闭环增益有关还是和环路增益有关，以及是应该闭环仿真还是开环仿真。

我们应该首先了解放大器的稳定性问题，放大器在使用时一般接成负反馈的形式，而在接成负反馈系统之后就会存在稳定性问题，因为在负反馈系统是其闭环增益为：

其中H(S)为前馈放大器增益，β为反馈系数，如果在某一频率处 $\beta H(S)=-1$ ，则产生的闭环增益会变为无穷大，使得电路中的噪声放大直到振荡，所以负反馈系统中会存在稳定性问题。为此提出了巴克豪森判据，如下：（即 $\beta H(j\omega )=-1$ 的另一种表达）

从上述判据中可以看出，反馈系统的稳定性是和环路增益有关的，而不是和闭环增益有关，所得到的波特图可用于对稳定性做出判断（注：波特图的纵轴是环路增益），如下所示是稳定和不稳定电路的两种波特图：

对于稳定的系统要求其增益交点频率要小于相位交点频率（相位裕度一般要大于60°）

现在我们知道了稳定性是和环路增益有关的，那么如何求环路增益呢？

环路增益的计算一般按照下面的方法进行，如下图所示：

将主输入置零（交流信号置零，保留直流偏置），在某点断开环路，在“顺时针方向”注入一个测试信号，使信号沿环路环绕，直到回到这个断点，我们得到一个电压值，与测试电压相比可以得到传输函数，该传输函数的负值就是环路增益。这里想问个问题如果β=1，岂不是说就相当于在前馈放大器的输入端加上测试信号，那得到的传输函数不就是开环传输函数吗？那在开环情况下得到的输出电压与输入电压的比值与频率的关系不就是环路增益与频率的关系吗？（即波特图）

现在我们需要知道AC仿真的原理是啥？

在AC仿真中可以绘制出的四种曲线如下所示：

Magnitude表示的是输出信号的幅度，Phase表示的是输出信号的相位，dB10表示的是 $10\log_{10}\left ( V_{OUT} \right )$ ，dB20表示的是 $20\log_{10}( V_{OUT} )$ ，而在输入的交流信号为1V时 $20\log_{10}\left ( V_{OUT} \right )$ 就可以表示为 $20\log_{10}\left ( V_{OUT} /V_{IN}\right )$ ，因此我们常常令输入的交流信号为1V，这样画出的dB20曲线就是其开环情况下增益与频率的关系曲线，如果环路增益为1，这个曲线就可以代表环路增益的曲线，也就是波特图，由此我们可以得到与电路稳定性相关的一些数据。

然而通过这种方法所得到的与稳定有关的数据存在一定误差，尤其是没有在断点处加大电容电感。我们有如下的结论：

稳定性一律用闭环跑，开环没有意义

stb在哪里插iprobe都可以，cadence也推荐用这个方法跑；

ac需要在闭环的情况下找个点断开环路然后加大电容大电感，这个断点最好是高阻低电容的，比如运放的输入，否则会有误差

【解释】加iprobe的方式是MIiddlebrook Method，[1][2]环路增益的公式是

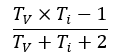
其中 $T_{V}$ ， $T_{i}$ 分别是电压增益和电流增益，而ac方式测量的只是电压增益 $T_{V}$ 。如果采用ac方式在高阻点断开环路，那 $T_{i}$ 近似为无穷。这种情况下ac和stb方式测得的环路增益基本一致，但是高频会有区别。如果采用ac方式但是没有在高阻点断开环路，这样 $T_{i}$ 就不是无穷了，这时候ac和stb测量的环路增益在低频下就会出现区别，此时ac方式得到的环路增益是不准确的。

接着我们利用一个密勒补偿的两级放大器来验证以下情况：

①、ac仿真——开环仿真

②、ac仿真——闭环仿真但不加大电容大电感

③、ac仿真——闭环仿真加大电容大电感

④、stb仿真——闭环仿真

1、ac开环仿真

在这里又遇到了一个问题：ac输出的结果是 $V_{OUT}$ ，对于单端输入单端输出的放大器来说当输入的ac电压幅度为1V时其输出的电压就可以代表其电压增益；而对于差分输入单端输出的放大器来说，其增益的表达式就不是简单的 $V_{OUT}/V_{IN}$ 了，直接给ac激励源一个1V的ac信号所得到的结果就不能够代表放大器的电压增益。为了解决这个问题我们应该首先了解对于差分放大器其增益具体是如何表达的？

对于差分放大器其存在三个增益，分别是差模增益，共模增益和共模到差模的增益，其中差模增益是我们期待的增益，其表达式为：

对于差分输入差分输出放大器为：

对于差分输入单端输出放大器为：

而共模增益是在电流源为有限阻抗时出现的输入共模电平的变化引起的输出共模电平的变化，（注：在此失配下其差分输出的共模电压是相同的，可以短接）表达式为：

而共模到差模的增益是在电路出现是失配时出现的输入共模电平的变化在输出产生了差模变化，其表达式为：

（注：对于差分输入单端输出，共模电平的变化还能引起共模增益和共模到差模增益吗？可以想象的是共模电平的变化会引起共模增益，但是似乎共模到差模的增益是难以想象的。所以这里我们应该知道双端输出的全差分放大器其共模抑制比： $CMRR=A_{DM}/A_{CM-DM}$ ，而对于单端输出的差分放大器其共模抑制比： $CMRR=A_{DM}/A_{CM}$ ）

所以在ac仿真差分放大器时，为了使得到的输出电压可以代表电压增益我们应该使 $V_{IN2}-V_{IN1}=1V$ ，这样得到的输出电压就可以代表电压增益，可以给 $V_{IN2}=0.5V,V_{IN1}=-0.5V$ 。这里指小信号ac电压。

（当然你也可以选择 $V_{IN2}=1V,V_{IN1}=0V$ 等，只要差值为1V即可，对得到的增益结果没有影响）

下面我们对下述电路进行仿真：

首先我们给定 $V_{P}=0.5V,V_{N}=-0.5V$ 得到的结果如下所示：

我们再给定 $V_{P}=1V,V_{N}=0V$ 得到结果如下所示：

再给定 $V_{P}=0.7V,V_{N}=-0.3V$ 得到结果如下所示：

从上述的三个仿真结果可以看出我们给出的两种输入情况的增益仿真结果是相同的，但是在相位上存在一定的误差。（为什么？可能和仿真中使用的小信号模型有关，输出信号的相位对两个输入的依赖关系不同，不过不确定，或许可以做个小信号推导输出信号和输入信号的相位关系）

2、ac闭环仿真——不加大电容大电感

其仿真的电路图如下所示：

直接将输出接在负输入端，输入信号的ac幅值设为1V，得到：

可以看到其输出信号的幅值近似为1V,dB值接近0

3、ac闭环仿真——加大电容大电感

这里其实有个困惑如何加大电容大电感，我在查找资料后找到

上述所示的解释，即不仅可以加大电感也可以加大电阻，其串联在反馈回路中，而电容则并联在输入端，这样就产生了一个直流时短路交流时开路的负反馈结构，从而可以做直流分析，在查找资料时还看到下面的论述：

论述了串联电感和电阻的主要优缺点。

仿真大电感大电容的原理图如下：

得到结果为：

感觉得到的结果好奇怪，我们试图给电感加上寄生电阻得到的结果如下所示：

看起来就正常了点，接着我们用电阻加电容仿真，得到：

可以看到这个和上面的电感加寄生电阻和电容的接法的仿真结果完全相同，同时和上面的闭环无电感电容的方法相比其出现了不同的增益情况，表明加电容电感和不加电容电感是完全不同的。主要就在于创建了一个交流时开路的反馈结构。

4、stb闭环仿真

其仿真电路图如下所示：

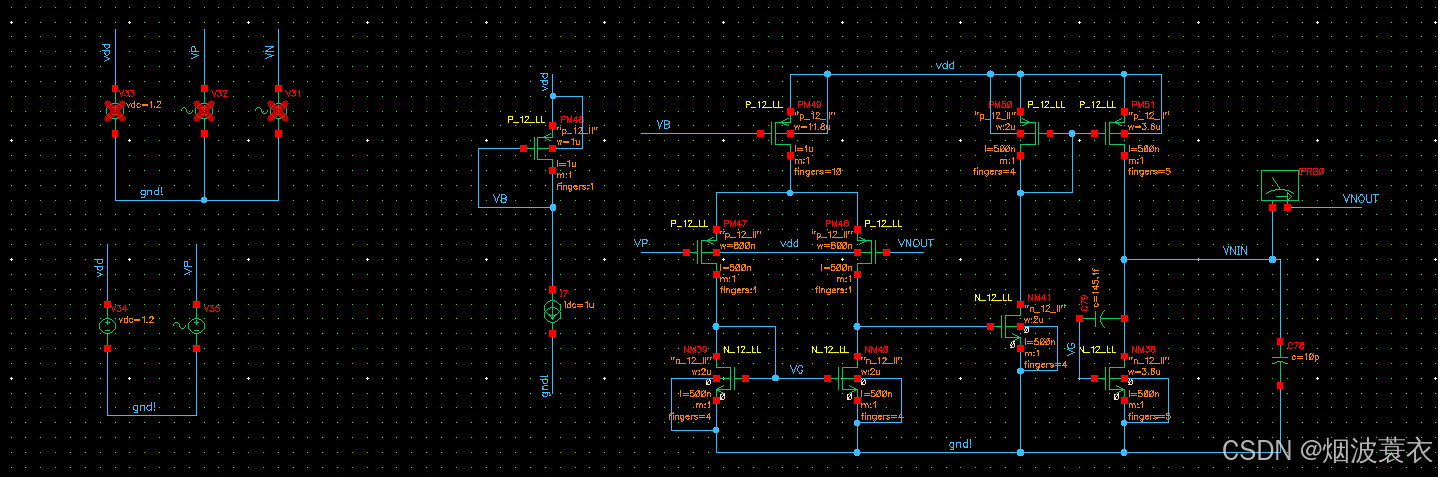
仿真得到的结果如下所示：

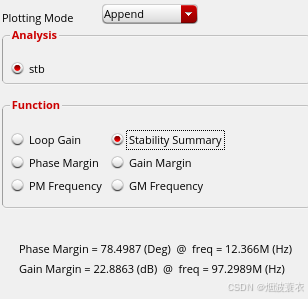
可以看出这和开环仿真的结果差别较大而和闭环加大电阻电容的方法虽然存在一定差距，但是差距不是很大，所以从上述论断我们可以得到：

正确的仿真环路稳定性的方法是stb仿真，再次是闭环加大电阻电容的方法【这里要注意在什么地方断开环路再加大电阻大电容】（闭环不加电阻电容以及开环测量得到的增益都是一种错误的绘制波特图的方法）

【在交流仿真中打破闭环的正确方法：

我们以一种典型的反馈结构作为示例，该电路结构如下所示：

当打破闭环时，为了构建更加准确的模型，断点处的输出阻抗和输入阻抗都应该被考虑到。如下图所示：

模块β的输出阻抗 $Z_{o,\beta }$ 被插入到打断点的前端处，而模块A的输入阻抗 $Z_{i,A }$ 被加到打断点的后端。按照下图所示连接电感和电容就可以通过仿真提取传递函数：

电感L用来传导直流信号，以保持直流工作电压的稳定，同时也隔断了交流信号，因此从小信号的角度来看就形成了一个开环电路。与之对比，电容C只传导交流测试信号，阻碍直流信号的传输。X处的直流电压不会受到交流信号的影响。传递函数能够通过观察 $v_{FB}/v_{ac}$ 的值得到。

但是，推导出输出/输入阻抗的准确值既不容易，也不方便。因此一个打破闭环的可能的方法是选择一个高阻抗的结点作为打断点，来减小分析过程的复杂度。正是我们上面仿真所使用的断开环路的方法，但是有时很难在环路中找到高阻抗结点，因此提出了下述仿真电路：

直流分析时，每个电路模块的直流工作点都被设定在如下图所示的位置：

而在考虑交流情况时，电路模块呈现出开路特性，如下所示：

虚拟电路用于提供 $Z_{i,A }$ 。相应的我们就可以确认电路的直流和交流特性。这个方法可以得到一个不受打断点选择影响的准确模型，类似的，传递函数能够通过观察 $v_{FB,1}/v_{ac}$ 的值得到。

】

[1] Middlebrook, R.D., "Measurement of Loop Gain in Feedback Systems", Int. J. Electronics, vol 38, No. 4, pp. 485-512, 1975

[2]Michael Tian, V. Visvanathan, Jeffrey Hantgan, and Kenneth Kundert,"Striving for Small-Signal Stability", IEEE Circuits and Devices Magazine,vol. 17, no. 1, pp. 31-41, January 2001.

[3]集成电路设计中的电源管理技术/陈科宏著；陈铖颖等译.—北京：机械工业出版社，2020.4