Uniform continuity

In mathematics, a real function {\displaystyle f}f of real numbers is said to be uniformly continuous if there is a positive real number {\displaystyle \delta }\delta such that function values over any function domain interval of the size {\displaystyle \delta }\delta are as close to each other as we want. In other words, for a uniformly continuous real function of real numbers, if we want function value differences to be less than any positive real number {\displaystyle \epsilon }\epsilon , then there is a positive real number {\displaystyle \delta }\delta such that {\displaystyle |f(x)-f(y)|<\epsilon }{\displaystyle |f(x)-f(y)|<\epsilon } at any {\displaystyle x}x and {\displaystyle y}y in any function interval of the size {\displaystyle \delta }\delta .

The difference between uniform continuity and (ordinary) continuity is that, in uniform continuity there is a globally applicable {\displaystyle \delta }\delta (the size of a function domain interval over which function value differences are less than {\displaystyle \epsilon }\epsilon ) that depends on only {\displaystyle \varepsilon }\varepsilon , while in (ordinary) continuity there is a locally applicable {\displaystyle \delta }\delta that depends on the both {\displaystyle \varepsilon }\varepsilon and {\displaystyle x}x. So uniform continuity is a stronger continuity condition than continuity; a function that is uniformly continuous is continuous but a function that is continuous is not necessarily uniformly continuous. The concepts of uniform continuity and continuity can be expanded to functions defined between metric spaces.

Continuous functions can fail to be uniformly continuous if they are unbounded on a bounded domain, such as {\displaystyle f(x)={\tfrac {1}{x}}}{\displaystyle f(x)={\tfrac {1}{x}}} on {\displaystyle (0,1)}(0,1), or if their slopes become unbounded on an infinite domain, such as {\displaystyle f(x)=x^{2}}f(x)=x{2} on the real (number) line. However, any Lipschitz map between metric spaces is uniformly continuous, in particular any isometry (distance-preserving map).

Although continuity can be defined for functions between general topological spaces, defining uniform continuity requires more structure. The concept relies on comparing the sizes of neighbourhoods of distinct points, so it requires a metric space, or more generally a uniform space.

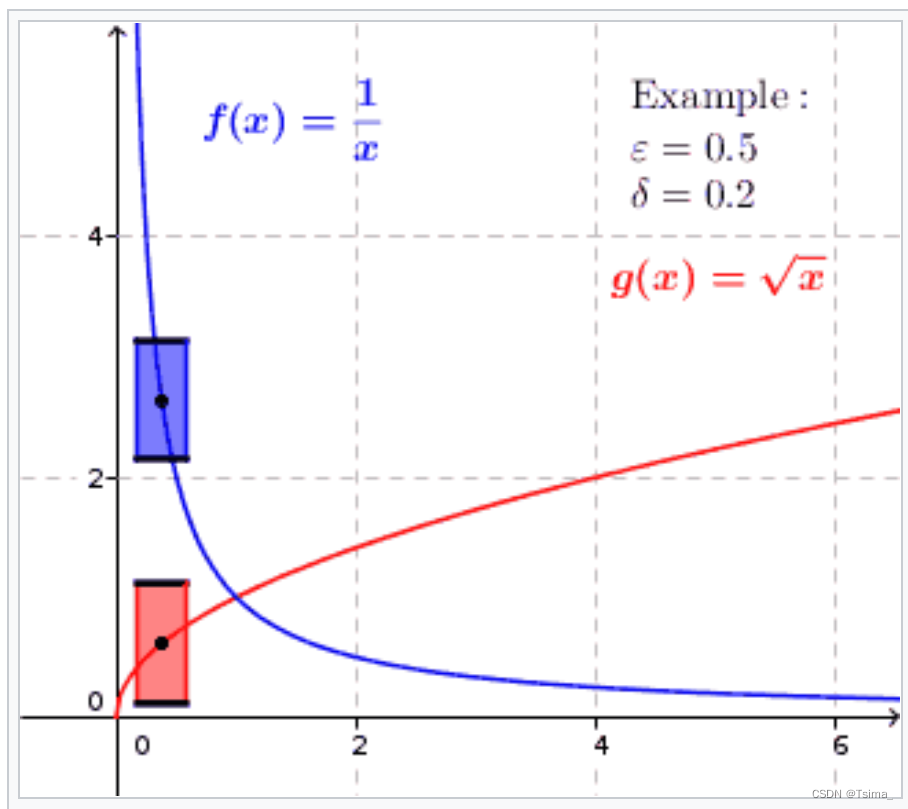
At some point the graph of {\displaystyle f(x)={\tfrac {1}{x}}}{\displaystyle f(x)={\tfrac {1}{x}}} will penetrate the top and/or bottom of a (here blue) window with height {\displaystyle 2\varepsilon \in \mathbb {R} _{>0}}{\displaystyle 2\varepsilon \in \mathbb {R} _{>0}} and width {\displaystyle 2\delta \in \mathbb {R} _{>0}}{\displaystyle 2\delta \in \mathbb {R} _{>0}} while {\displaystyle (f)}(f) ranging over an interval less than that width, as that window’s center moves over the graph in the direction of {\displaystyle x=0}{\displaystyle x=0}. If there existed a window whereof top and/or bottom is not penetrated by this graph as the window moves over the graph in the direction of {\displaystyle x=0}x=0, then its width would be infinitesimally small, so {\displaystyle f(x)}f(x) is not uniformly continuous. The function {\displaystyle g(x)={\sqrt {x}}}{\displaystyle g(x)={\sqrt {x}}}, on the other hand, is uniformly continuous.

1 Definition for functions on metric spaces

For a function {\displaystyle f:X\to Y}f:X\to Y with metric spaces {\displaystyle (X,d_{1})}{\displaystyle (X,d_{1})} and {\displaystyle (Y,d_{2})}{\displaystyle (Y,d_{2})}, the following definitions of uniform continuity and (ordinary) continuity hold.

1.1 Definition of uniform continuity

{\displaystyle f}f is called uniformly continuous if for every real number {\displaystyle \varepsilon >0}\varepsilon >0 there exists a real number {\displaystyle \delta >0} \delta > 0 such that for every {\displaystyle x,y\in X}{\displaystyle x,y\in X} with {\displaystyle d_{1}(x,y)<\delta }{\displaystyle d_{1}(x,y)<\delta }, we have {\displaystyle d_{2}(f(x),f(y))<\varepsilon }{\displaystyle d_{2}(f(x),f(y))<\varepsilon }. The set {\displaystyle {y\in X:d_{1}(x,y)<\delta }}{\displaystyle {y\in X:d_{1}(x,y)<\delta }} for each {\displaystyle x}x is a neighbourhood of {\displaystyle x}x and the set {\displaystyle {x\in X:d_{1}(x,y)<\delta }}{\displaystyle {x\in X:d_{1}(x,y)<\delta }} for each {\displaystyle y}y is a neighbourhood of {\displaystyle y}y by the definition of a neighbourhood in a metric space.
If {\displaystyle X}X and {\displaystyle Y}Y are subsets of the real line, then {\displaystyle d_{1}} d_1 and {\displaystyle d_{2}} d_2 can be the standard one-dimensional Euclidean distance, yielding the following definition: for every real number {\displaystyle \varepsilon >0}\varepsilon >0 there exists a real number {\displaystyle \delta >0} \delta > 0 such that for every {\displaystyle x,y\in X}{\displaystyle x,y\in X}, {\displaystyle |x-y|<\delta \implies |f(x)-f(y)|<\varepsilon }{\displaystyle |x-y|<\delta \implies |f(x)-f(y)|<\varepsilon } (where {\displaystyle A\implies B}{\displaystyle A\implies B} is a material conditional statement saying “if {\displaystyle A}A, then {\displaystyle B}B”).
Equivalently, {\displaystyle f}f is said to be uniformly continuous if {\displaystyle \forall \varepsilon >0;\exists \delta >0;\forall x\in X;\forall y\in X:,d_{1}(x,y)<\delta ,\Rightarrow ,d_{2}(f(x),f(y))<\varepsilon }{\displaystyle \forall \varepsilon >0;\exists \delta >0;\forall x\in X;\forall y\in X:,d_{1}(x,y)<\delta ,\Rightarrow ,d_{2}(f(x),f(y))<\varepsilon }. Here quantifications ({\displaystyle \forall \varepsilon >0}{\displaystyle \forall \varepsilon >0}, {\displaystyle \exists \delta >0}{\displaystyle \exists \delta >0}, {\displaystyle \forall x\in X}{\displaystyle \forall x\in X}, and {\displaystyle \forall y\in X}{\displaystyle \forall y\in X}) are used.
Alternatively, {\displaystyle f}f is said to be uniformly continuous if there is a function of all positive real numbers {\displaystyle \varepsilon }\varepsilon , {\displaystyle \delta (\varepsilon )}\delta(\varepsilon) representing the maximum positive real number, such that for every {\displaystyle x,y\in X}{\displaystyle x,y\in X} if {\displaystyle d_{1}(x,y)<\delta (\varepsilon )}{\displaystyle d_{1}(x,y)<\delta (\varepsilon )} then {\displaystyle d_{2}(f(x),f(y))<\varepsilon }{\displaystyle d_{2}(f(x),f(y))<\varepsilon }. {\displaystyle \delta (\varepsilon )}\delta(\varepsilon) is a monotonically non-decreasing function.

1.2 Definition of (ordinary) continuity

{\displaystyle f}f is called continuous {\displaystyle {\underline {{\text{at }}x}}}{\displaystyle {\underline {{\text{at }}x}}} if for every real number {\displaystyle \varepsilon >0}\varepsilon >0 there exists a real number {\displaystyle \delta >0} \delta > 0 such that for every {\displaystyle y\in X} y \in X with {\displaystyle d_{1}(x,y)<\delta }{\displaystyle d_{1}(x,y)<\delta }, we have {\displaystyle d_{2}(f(x),f(y))<\varepsilon }{\displaystyle d_{2}(f(x),f(y))<\varepsilon }. The set {\displaystyle {y\in X:d_{1}(x,y)<\delta }}{\displaystyle {y\in X:d_{1}(x,y)<\delta }} is a neighbourhood of {\displaystyle x}x. Thus, (ordinary) continuity is a local property of the function at the point {\displaystyle x}x.
Equivalently, a function {\displaystyle f}f is said to be continuous if {\displaystyle \forall x\in X;\forall \varepsilon >0;\exists \delta >0;\forall y\in X:,d_{1}(x,y)<\delta ,\Rightarrow ,d_{2}(f(x),f(y))<\varepsilon }{\displaystyle \forall x\in X;\forall \varepsilon >0;\exists \delta >0;\forall y\in X:,d_{1}(x,y)<\delta ,\Rightarrow ,d_{2}(f(x),f(y))<\varepsilon }.
Alternatively, a function {\displaystyle f}f is said to be continuous if there is a function of all positive real numbers {\displaystyle \varepsilon }\varepsilon and {\displaystyle x\in X}x\in X, {\displaystyle \delta (\varepsilon ,x)}{\displaystyle \delta (\varepsilon ,x)} representing the maximum positive real number, such that at each {\displaystyle x}x if {\displaystyle y\in X}y \in X satisfies {\displaystyle d_{1}(x,y)<\delta (\varepsilon ,x)}{\displaystyle d_{1}(x,y)<\delta (\varepsilon ,x)} then {\displaystyle d_{2}(f(x),f(y))<\varepsilon }{\displaystyle d_{2}(f(x),f(y))<\varepsilon }. At every {\displaystyle x}x, {\displaystyle \delta (\varepsilon ,x)}{\displaystyle \delta (\varepsilon ,x)} is a monotonically non-decreasing function.

2 Local continuity versus global uniform continuity

In the definitions, the difference between uniform continuity and continuity is that, in uniform continuity there is a globally applicable {\displaystyle \delta }\delta (the size of a neighbourhood in {\displaystyle X}X over which values of the metric for function values in {\displaystyle Y}Y are less than {\displaystyle \varepsilon }\varepsilon ) that depends on only {\displaystyle \varepsilon }\varepsilon while in continuity there is a locally applicable {\displaystyle \delta }\delta that depends on the both {\displaystyle \varepsilon }\varepsilon and {\displaystyle x}x. Continuity is a local property of a function — that is, a function {\displaystyle f}f is continuous, or not, at a particular point {\displaystyle x}x of the function domain {\displaystyle X}X, and this can be determined by looking at only the values of the function in an arbitrarily small neighbourhood of that point. When we speak of a function being continuous on an interval, we mean that the function is continuous at every point of the interval. In contrast, uniform continuity is a global property of {\displaystyle f}f, in the sense that the standard definition of uniform continuity refers to every point of {\displaystyle X}X. On the other hand, it is possible to give a definition that is local in terms of the natural extension {\displaystyle f^{*}}f{*}(the characteristics of which at nonstandard points are determined by the global properties of {\displaystyle f}f), although it is not possible to give a local definition of uniform continuity for an arbitrary hyperreal-valued function, see below.

A mathematical definition that a function {\displaystyle f}f is continuous on an interval {\displaystyle I}I and a definition that {\displaystyle f}f is uniformly continuous on {\displaystyle I}I are structurally similar as shown in the following.

Continuity of a function {\displaystyle f:X\to Y}f:X\to Y for metric spaces {\displaystyle (X,d_{1})}{\displaystyle (X,d_{1})} and {\displaystyle (Y,d_{2})}{\displaystyle (Y,d_{2})} at every point {\displaystyle x}x of an interval {\displaystyle I\subseteq X}{\displaystyle I\subseteq X} (i.e., continuity of {\displaystyle f}f on the interval {\displaystyle I}I) is expressed by a formula starting with quantifications

{\displaystyle \forall \varepsilon >0;\forall x\in I;\exists \delta >0;\forall y\in I:,d_{1}(x,y)<\delta ,\Rightarrow ,d_{2}(f(x),f(y))<\varepsilon }{\displaystyle \forall \varepsilon >0;\forall x\in I;\exists \delta >0;\forall y\in I:,d_{1}(x,y)<\delta ,\Rightarrow ,d_{2}(f(x),f(y))<\varepsilon },
(metrics {\displaystyle d_{1}(x,y)}{\displaystyle d_{1}(x,y)} and {\displaystyle d_{2}(f(x),f(y))}{\displaystyle d_{2}(f(x),f(y))} are {\displaystyle |x-y|}{\displaystyle |x-y|} and {\displaystyle |f(x)-f(y)|}{\displaystyle |f(x)-f(y)|} for {\displaystyle f:\mathbb {R} \to \mathbb {R} }f:{\mathbb {R}}\to {\mathbb {R}} for the set of real numbers {\displaystyle \mathbb {R} }{\mathbb {R}}).

For uniform continuity, the order of the first, second, and third quantifications ({\displaystyle \forall x\in I}{\displaystyle \forall x\in I}, {\displaystyle \forall \varepsilon >0}{\displaystyle \forall \varepsilon >0}, and {\displaystyle \exists \delta >0}{\displaystyle \exists \delta >0}) are rotated:

{\displaystyle \forall \varepsilon >0;\exists \delta >0;\forall x\in I;\forall y\in I:,d_{1}(x,y)<\delta ,\Rightarrow ,d_{2}(f(x),f(y))<\varepsilon }{\displaystyle \forall \varepsilon >0;\exists \delta >0;\forall x\in I;\forall y\in I:,d_{1}(x,y)<\delta ,\Rightarrow ,d_{2}(f(x),f(y))<\varepsilon }.
Thus for continuity on the interval, one takes an arbitrary point {\displaystyle x}x of the interval, and then there must exist a distance {\displaystyle \delta }\delta ,

{\displaystyle \cdots \forall x,\exists \delta \cdots ,}\cdots \forall x,\exists \delta \cdots ,
while for uniform continuity, a single {\displaystyle \delta }\delta must work uniformly for all points {\displaystyle x}x of the interval,

{\displaystyle \cdots \exists \delta ,\forall x\cdots .}{\displaystyle \cdots \exists \delta ,\forall x\cdots .}

3 Properties

4 Examples and nonexamples

4.1 Examples

4.2 Nonexamples

5 Visualization

6 History

7 Other characterizations

7.1 Non-standard analysis

7.2 Cauchy continuity

8 Relations with the extension problem

9 Generalization to topological vector spaces

10 Generalization to uniform spaces

11 See also