Harris角点检测原理及库实现

SukiAme

已于 2024-04-26 11:54:03 修改

阅读量1.7k

点赞数 30

文章标签： opencv 人工智能计算机视觉

于 2024-04-26 11:51:58 首次发布

本文链接：https://blog.csdn.net/qq_67037885/article/details/138212388

版权

今天主要讲原理以及如何用OpenCV库实现，大家如果有兴趣下期可以出算法代码实现。

角点(Corner Points)

通常意义上来说，角点就是极值点，即在某方面属性特别突出的点，是在某些属性上强度最大或者最小的孤立点、线段的终点。对于图像而言，角点是指物体边缘的拐点(交点)，它是一种非常重要的局部特征，决定了图像中目标的形状，所以在图像匹配、目标描述与识别以及运动估计、目标跟踪等领域，角点提取都具有十分重要的意义。

1.Harris角点检测

利用矩形窗在图像上移动，若窗内包含有角点，则窗口向各个方向移动进而利用这一规律实现图像角点检测的目时，窗内的灰度值都会发生变化。具体地，考虑以下三种情况:

从数学角度来看，Harris角点检测算法受信号处理中自相关函数的启发，设计了以下自相关函数来描述局部窗口的亮度变化:

(u,v)代表当前待判定的像素点，△x,△y 分别是水平、垂直方向上的偏移量; I(x, y)代表图像 I在点(x,y)的亮度值; w(x,y)是局部窗口加权函数，有高斯加权和均值加权等。

但是如何求解平移后的图像灰度呢？

需要用到高数中的泰勒展开式：

再将其带入原来的亮度变化公式：

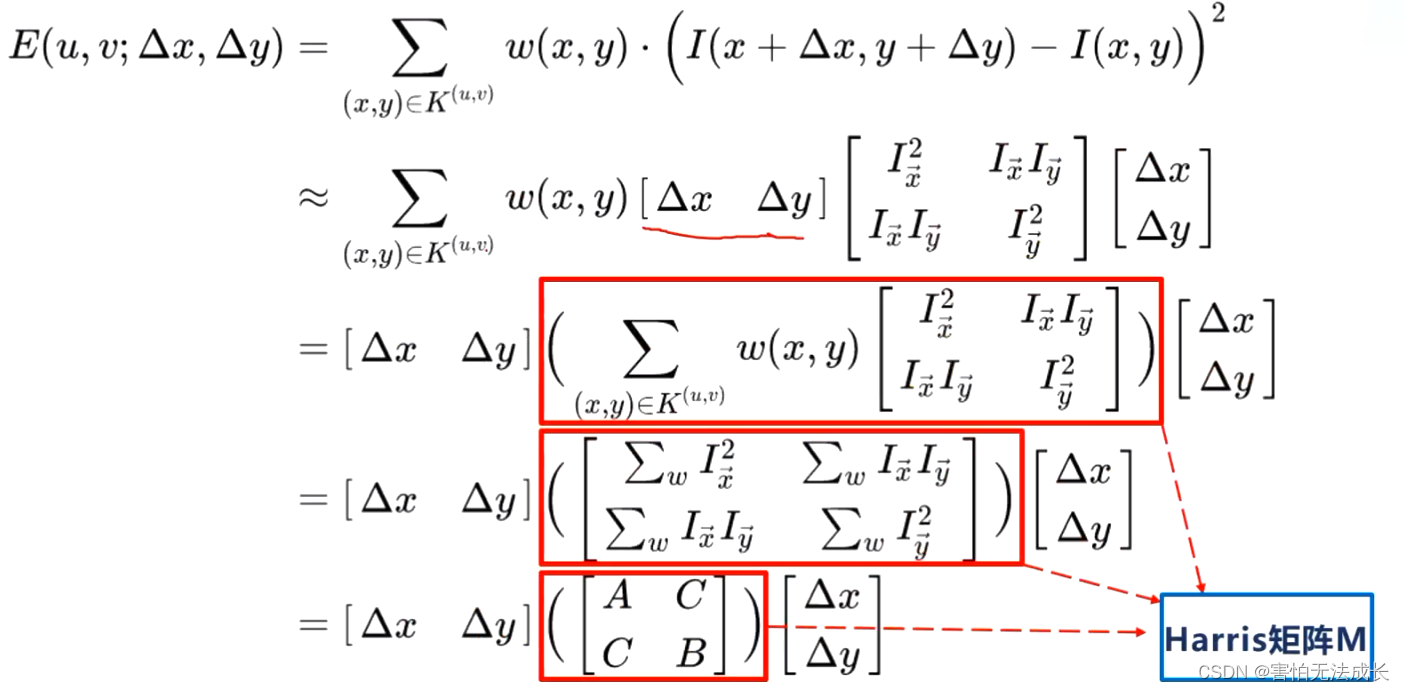
1.1Harris矩阵M

将公式展开，可以发现交叉项为0时，即C=0,令表达式等于常数Q，则其为一个椭圆。

此时局部区域的域的梯度方向信息都集中在主对角线上，入1表征了x方向的梯度信息，入2表征了y方向的梯度. 有如下结论：

但是上述结论是交叉项C=0得出的，如果C不为0呢？

我们可以采用线性代数的方法。此时，我们可以通过对Harris矩阵M进行正交相似对角化来消除交叉项，从而将坐标轴旋转到实际椭圆对应的梯度方向上。如下：

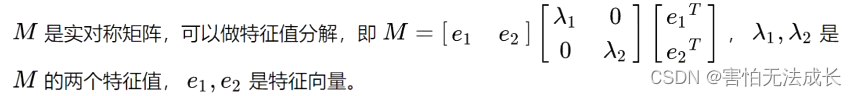
带入亮度变化公式：

展开上式：

可以看到，只有入1和入2都为较大值时E才能取到较大数，此时(u,v)为角点.综上所述，我们可以有如下结论：

M矩阵的两个特征值入1、入2的大小相对关系可以判断角点，即：

1.2如何界定特征值入1、入2的大小相对关系？

到底什么情况特征值入1、入2为较大值，什么情况为较小值？

角点响应函数

$\theta =det(M)-\alpha trace(M^{2})=\lambda _{1}\lambda _{2}-\alpha(\lambda _{1}+\lambda _{2})^{2}$

因此一般步骤为：

用OpenCV库函数调用示例：

cornerHarris(img,dst,blockSize,ksize,k) blockSize:检测窗口大小 ksize:sobel卷积核 k:权重系数，经验值，一般取0.02-0.04之间

import cv2
import numpy as np


blockSize=2
ksize=3
k=0.04
img=cv2.imread(r"C:\Users\86166\Desktop\corner2.png")
cv2.imshow("img",img)
#灰度 化   角点检测需要灰度图 否则 会报错
gray=cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

dst=cv2.cornerHarris(gray,blockSize,ksize,k)
print(dst.shape)
img[dst>0.01*dst.max()]=[0,0,255]

cv2.imshow('harris',img)
cv2.waitKey(0)

现象如下：