粒子群算法及蜂群算法求多维函数极值对比

1.粒子群算法

        1.1粒子群算法简单介绍

        粒子群优化算法源于对鸟群活动的研究。20 世纪 70 年代许多学者对鸟群的群体性活动进行了深入研究。生物学家 Reynolds 提出了 Boids模型,用来模拟鸟群聚集飞行的行为。在这个模型中每个个体都遵守三条规则：避免碰撞、速度一致,向中心聚集。该模型的仿真结果与自然界鸟群时而聚集时而分散的飞行特性基本一致。验证了鸟群个体的飞行轨迹与邻近个体的行为有关。生物学家 Erank Heppner对鸟群的趋同性进行了深入研究,建立了这样的鸟群运动模型:一群小鸟在空中漫无目的地飞行,当群体中的一只小鸟发现栖息地时,它会飞向这个栖息地,同时也会将它周围的小鸟吸引过来,而它周围的这些鸟也将影响群体中其他的小鸟,最终将整个鸟群引向这个栖息地。研究发现,鸟群的同步飞行只是建立在每只鸟对邻近鸟的局部感知,而并不存在一个集中控制者。

        1.2粒子群算法流程图

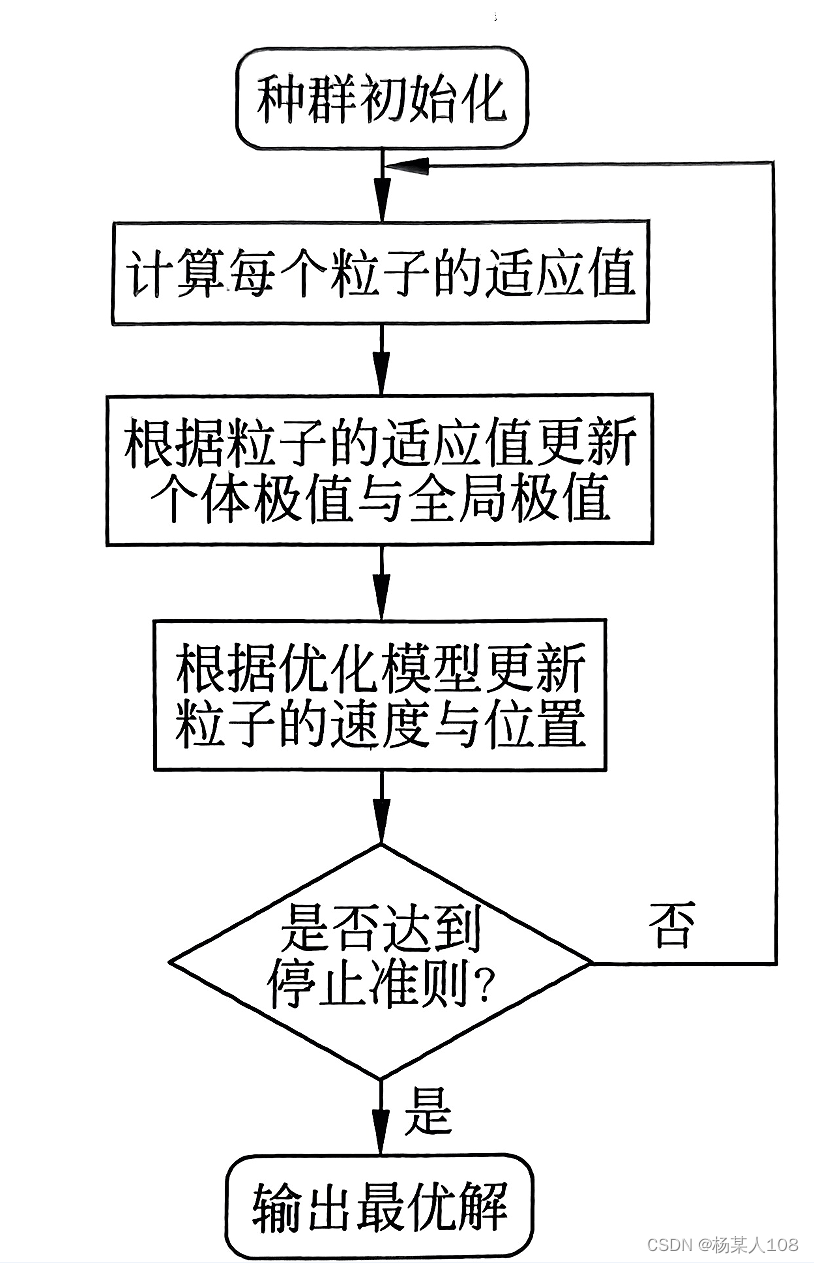
        1.3python代码求极小值

import math
import random
import numpy as np
import matplotlib.pyplot as plt
import pylab as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']


class PSO:
    def __init__(self, dimension, time, size, low, up, v_low, v_high):
        # 初始化
        self.dimension = dimension  # 变量个数
        self.time = time  # 迭代的代数
        self.size = size  # 种群大小
        self.bound = []  # 变量的约束范围
        self.bound.append(low)
        self.bound.append(up)
        self.v_low = v_low
        self.v_high = v_high
        self.x = np.zeros((self.size, self.dimension))  # 所有粒子的位置
        self.v = np.zeros((self.size, self.dimension))  # 所有粒子的速度
        self.p_best = np.zeros((self.size, self.dimension))  # 每个粒子最优的位置
        self.g_best = np.zeros((1, self.dimension))[0]  # 全局最优的位置

        # 初始化第0代初始全局最优解
        temp = -1000000
        for i in range(self.size):
            for j in range(self.dimension):
                self.x[i][j] = random.uniform(self.bound[0][j], self.bound[1][j])
                self.v[i][j] = random.uniform(self.v_low, self.v_high)
            self.p_best[i] = self.x[i]  # 储存最优的个体
            fit = self.fitness(self.p_best[i])
            # 做出修改
            if fit > temp:
                self.g_best = self.p_best[i]
                temp = fit

    #函数1
    def fitness(self, x):
        total=0
        for i in range(1,len(x)):
            total = total+x[i] 
        y=np.floor((total*100)/100)
        return y
    
    #函数2
    # def fitness(self, x):
    #     sun=0
    #     for i in range(1,len(x)):
    #         if i<len(x)-1:
    #             sun+=100*(x[i+1]-x[i]**2)**2+(x[i]-1)**2
    #     return sun
    
    #函数3
    # def fitness(self,x):  
    #     sun=0
    #     for i in range(1,len(x)):
    #         sun+=(x[i]**2-10*np.cos(2*np.pi*x[i])+10)
    #     sun=sun+10*len(x)
    #     return sun 
    
    #函数4
    # def fitness(self,x):  
    #     sun1=0
    #     sun2=1
    #     sun=0
    #     for i in range(1,len(x)):
    #         sun1+=x[i]**2
    #         sun2*=np.cos(x[i]/np.sqrt(i))
    #     sun=(1/400)*sun1-sun2+1
    #     return sun
    
    

    def update(self, size):
        c1 = 2.0  # 学习因子
        c2 = 2.0
        w = 0.8  # 自身权重因子
        for i in range(size):
            # 更新速度(核心公式)
            self.v[i] = w * self.v[i] + c1 * random.uniform(0, 1) * (
                    self.p_best[i] - self.x[i]) + c2 * random.uniform(0, 1) * (self.g_best - self.x[i])
            # 速度限制
            for j in range(self.dimension):
                if self.v[i][j] < self.v_low:
                    self.v[i][j] = self.v_low
                if self.v[i][j] > self.v_high:
                    self.v[i][j] = self.v_high

            # 更新位置
            self.x[i] = self.x[i] + self.v[i]
            # 位置限制
            for j in range(self.dimension):
                if self.x[i][j] < self.bound[0][j]:
                    self.x[i][j] = self.bound[0][j]
                if self.x[i][j] > self.bound[1][j]:
                    self.x[i][j] = self.bound[1][j]
            # 更新p_best和g_best
            if self.fitness(self.x[i]) < self.fitness(self.p_best[i]):
                self.p_best[i] = self.x[i]
            if self.fitness(self.x[i]) < self.fitness(self.g_best):
                self.g_best = self.x[i]

    def pso(self):
        best = []
        self.final_best = np.array([i for i in range(dimension)])
        for gen in range(self.time):
            self.update(self.size)
            if self.fitness(self.g_best) < self.fitness(self.final_best):
                self.final_best = self.g_best.copy()
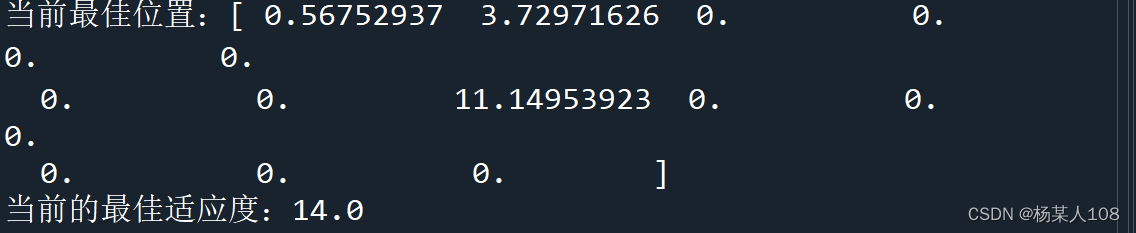
            print('当前最佳位置：{}'.format(self.final_best))
            temp = self.fitness(self.final_best)
            print('当前的最佳适应度：{}'.format(temp))
            best.append(temp)
        t = [i for i in range(self.time)]
#函数图像
        plt.figure()
        plt.plot(t, best, color='red', marker='.', ms=15)
        plt.rcParams['axes.unicode_minus'] = False
        plt.margins(0)
        plt.xlabel(u"迭代次数")  # X轴标签
        plt.ylabel(u"适应度")  # Y轴标签
        plt.title(u"迭代过程")  # 标题
        plt.show()


if __name__ == '__main__':
    time = 50
    size = 100
    dimension = 50
    v_low = -1
    v_high = 1
    low=[]
    up=[]
    for i in range(dimension):
        low.append(0)
        up.append(40)
    pso = PSO(dimension, time, size, low, up, v_low, v_high)
    pso.pso()

2.蜂群算法

        1.1蜂群算法简单介绍

       ABC算法利用蜜蜂觅食的自组织特性,通过蜜蜂不断地搜索和探索来完成解的更新。在现实的蜜蜂群中,蜂群包含三个基本要素：蜜源、雇佣蜂、非雇佣蜂，以及两种主要的行为模式；蜜源招募蜜蜂和放弃食物源。蜜源的好坏由多种因素决定,如蜜源到蜂巢的距离,蜂蜜的多少及开采的难易等。为了简单起见,用收益来表示蜜源的好坏。雇佣蜂是指正在某个蜜源采蜜或已经被这个蜜源雇佣的蜜蜂。它们会把这个蜜源的信息,如离蜂巢的距离和方向、蜜源的收益等通过舞蹈的方式告知其他的蜜蜂。非雇佣蜂包括侦查蜂和跟随蜂,侦查蜂四处探索寻找新的蜜源。一般来说,侦查蜂的数量为蜂群总数的 5％～10％。跟随蜂在舞蹈区等待由雇佣蜂带回的蜜源信息,根据舞蹈信息决定到哪个蜜源采蜜。较大收益的蜜源,可以招募到更多的蜜蜂去采蜜。

        1.2蜂群算法流程图

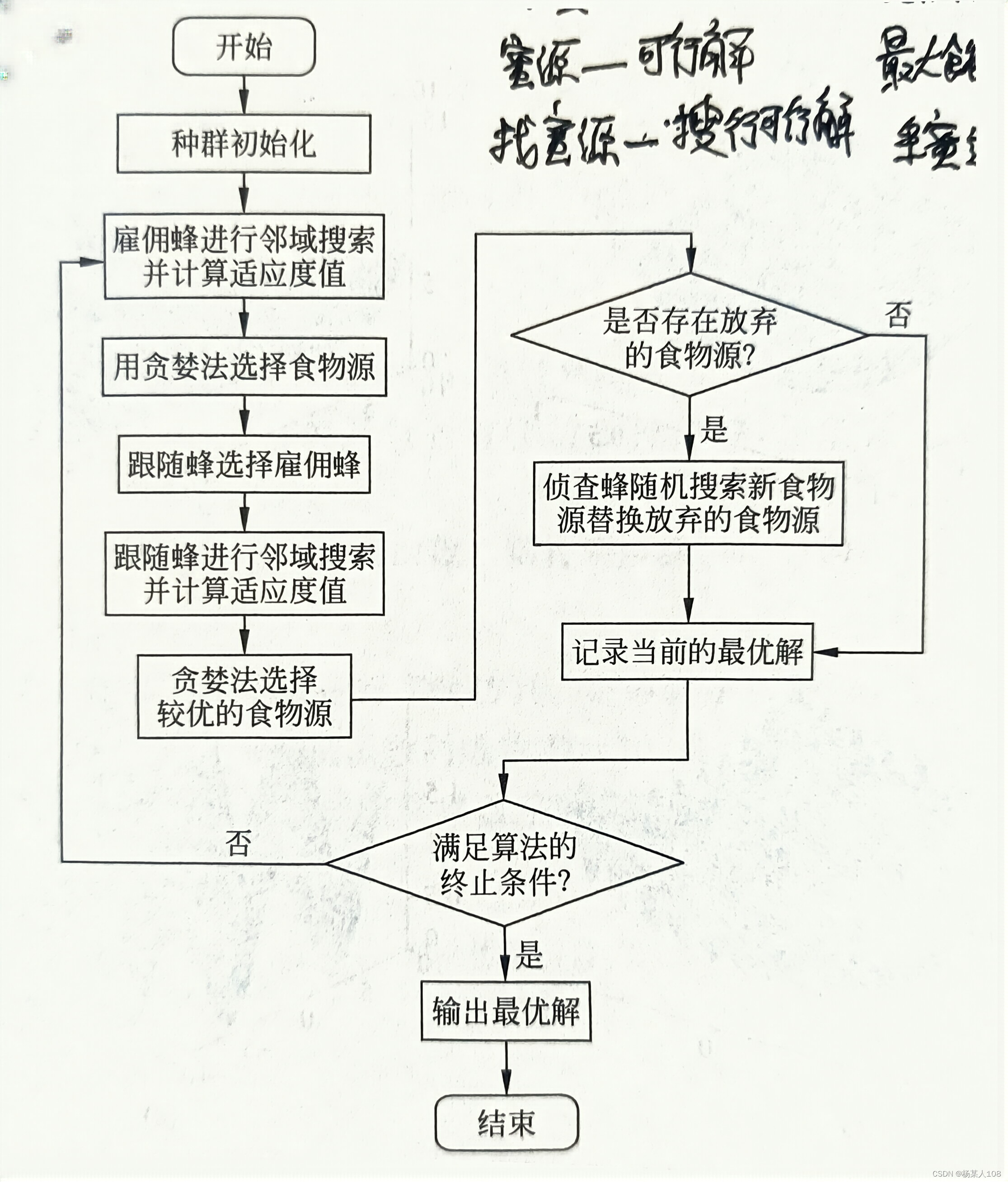
        1.3python代码求极小值

import numpy as np  
import random  
import matplotlib.pyplot as plt
#函数1
def objective_function(x): 
    total=0
    for i in range(1,len(x)):
        total = total+x[i] 
    y=np.floor((total*100)/100)
    return y

#函数2
# def objective_function(x): 
#     sun=0
#     for i in range(1,len(x)):
#         if i<len(x)-1:
#             sun+=100*(x[i+1]-x[i]**2)**2+(x[i]-1)**2
#     return sun

#函数3
# def objective_function(x): 
#     sun=0
#     for i in range(1,len(x)):
#         sun+=(x[i]**2-10*np.cos(2*np.pi*x[i])+10)
#     sun=sun+10*len(x)
#     return sun 

#函数4
# def objective_function(x):  
#     sun1=0
#     sun2=1
#     sun=0
#     for i in range(1,len(x)):
#         sun1+=x[i]**2
#         sun2*=np.cos(x[i]/np.sqrt(i))
#     sun=(1/400)*sun1-sun2+1
#     return sun

  
# ABC参数  
N = 50  # 蜜蜂总数（通常工蜂和观察蜂数量相等）  
D = 6 # 问题维度  
limit = 100  # 蜜源的最大迭代次数限制  
  
# 初始化蜜源（解）  
solutions = np.random.rand(N, D)  
fitness = np.array([objective_function(sol) for sol in solutions])  
trials = np.zeros(N, dtype=int)  # 记录蜜源被放弃的次数  

# ABC主循环  
for iter_count in range(limit):  
    # 工蜂阶段（搜索新蜜源）  
    for i in range(N):  
        # 选择一个随机蜜源作为邻居  
        j = random.randint(0, N-1)  
        while j == i:  
            j = random.randint(0, N-1)  
          
        # 在两个蜜源之间进行邻域搜索  
        phi = np.random.uniform(-1, 1, D)  
        new_solution = solutions[i] + phi * (solutions[i] - solutions[j])  
          
        # 检查新蜜源是否越界，并适当处理  
        new_solution = np.clip(new_solution, 0, 1)  # 假设解在[0,1]范围内  
          
        # 评估新蜜源的适应度  
        new_fitness = objective_function(new_solution)  
          
        # 如果新蜜源更好，则替换当前蜜源  
        if new_fitness < fitness[i]:  
            solutions[i] = new_solution  
            fitness[i] = new_fitness  
            trials[i] = 0  # 重置放弃次数  
        else:  
            trials[i] += 1  
      
    # 观察蜂阶段（选择蜜源并搜索）  
    # ...（与工蜂阶段类似，但选择是基于适应度的）  
      
    # 侦查蜂阶段（当蜜源被放弃多次后，随机生成新蜜源）  
    for i in range(N):  
        if trials[i] > limit:  
            solutions[i] = np.random.rand(D)  
            fitness[i] = objective_function(solutions[i])  
            trials[i] = 0  
      
    # 可以添加一些输出或收敛检查  
    # ...  

#画图
t = [i for i in range(N)]
plt.figure()
plt.plot(t, fitness, color='red', marker='.', ms=15)
plt.rcParams['axes.unicode_minus'] = False
plt.margins(0)
plt.xlabel(u"迭代次数")  # X轴标签
plt.ylabel(u"适应度")  # Y轴标签
plt.title(u"迭代过程")  # 标题
plt.show() 
      
  
# 输出最佳解  
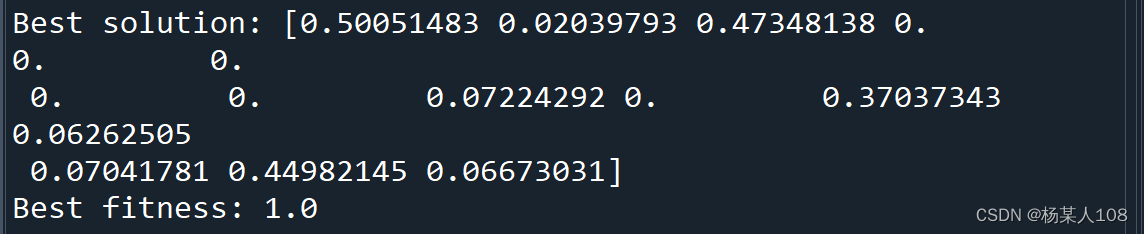
best_idx = np.argmin(fitness)  
print("Best solution:", solutions[best_idx])  
print("Best fitness:", fitness[best_idx])

3.多维度下极值对比

        3.1涉及多维函数

        代码涉及函数分别为以下四个函数：

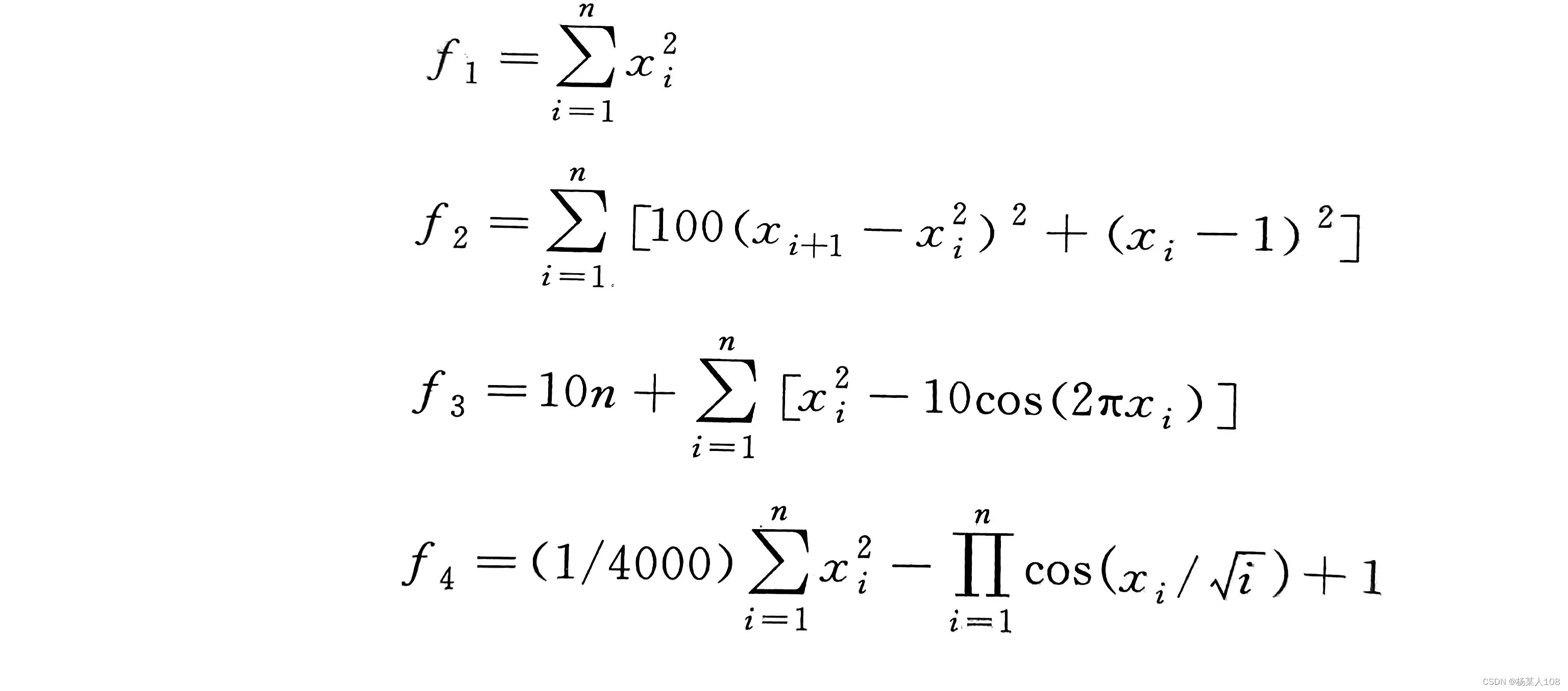
        3.2粒子群算法与蜂群算法各维度图像及输出值对比

           左边为粒子群算法，右边为蜂群算法，n为函数维度

  n=5时

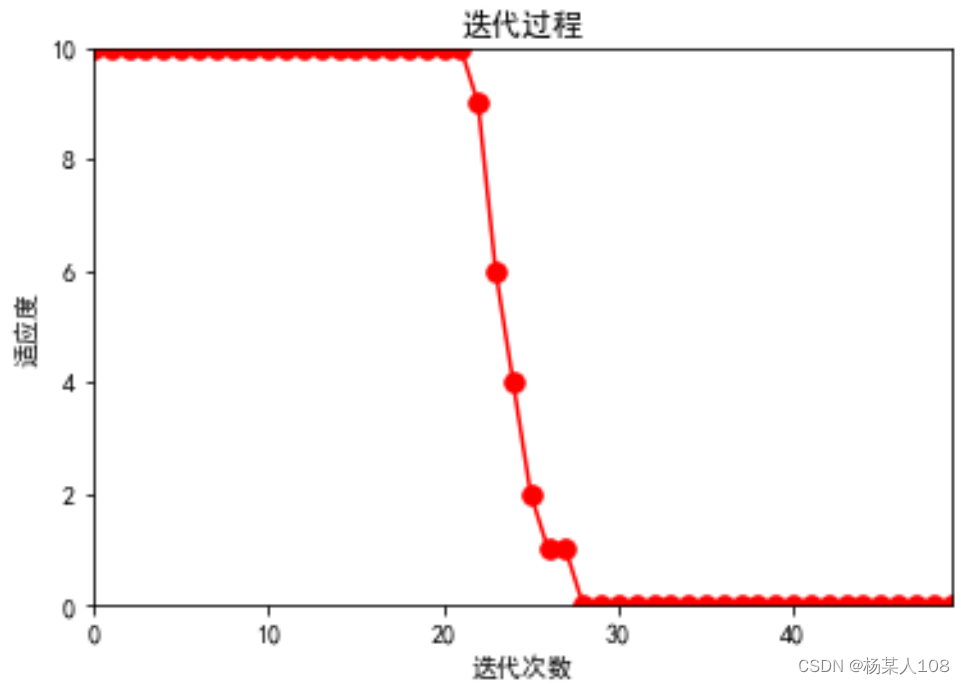
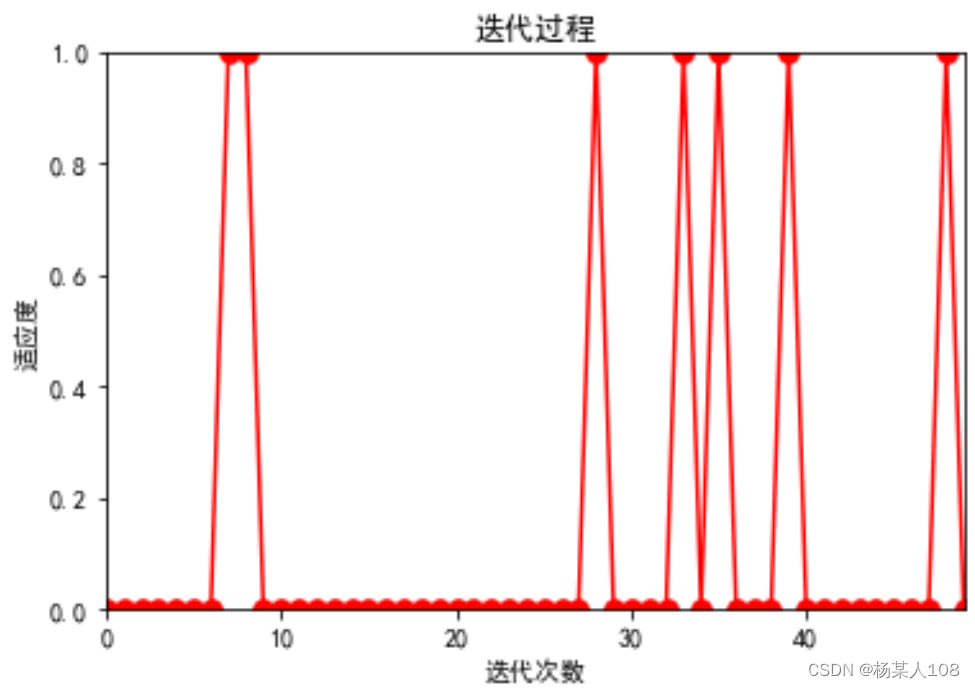
      n=10时

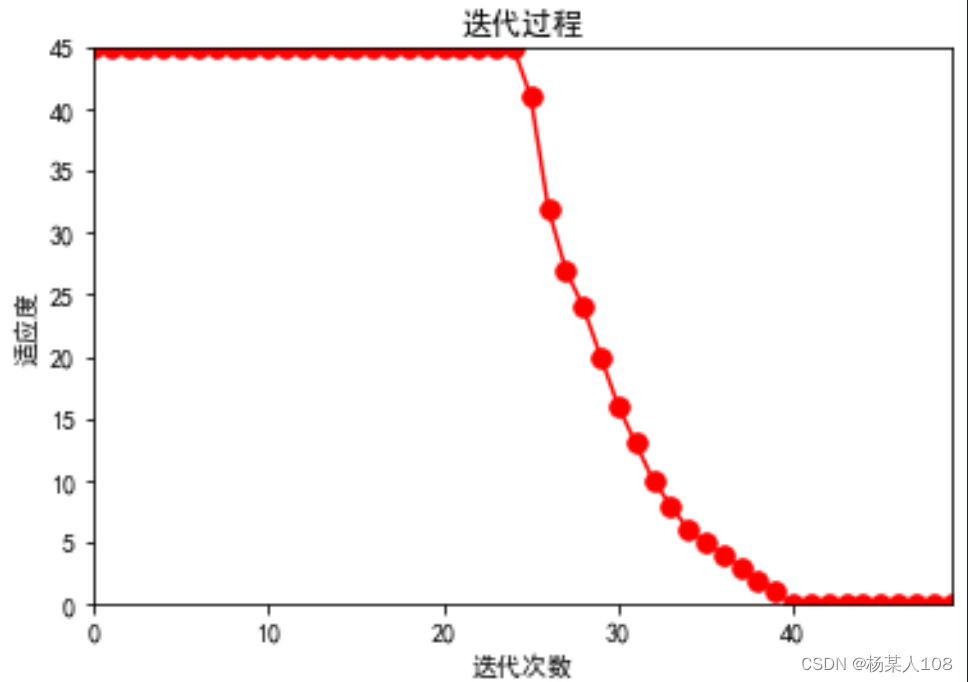
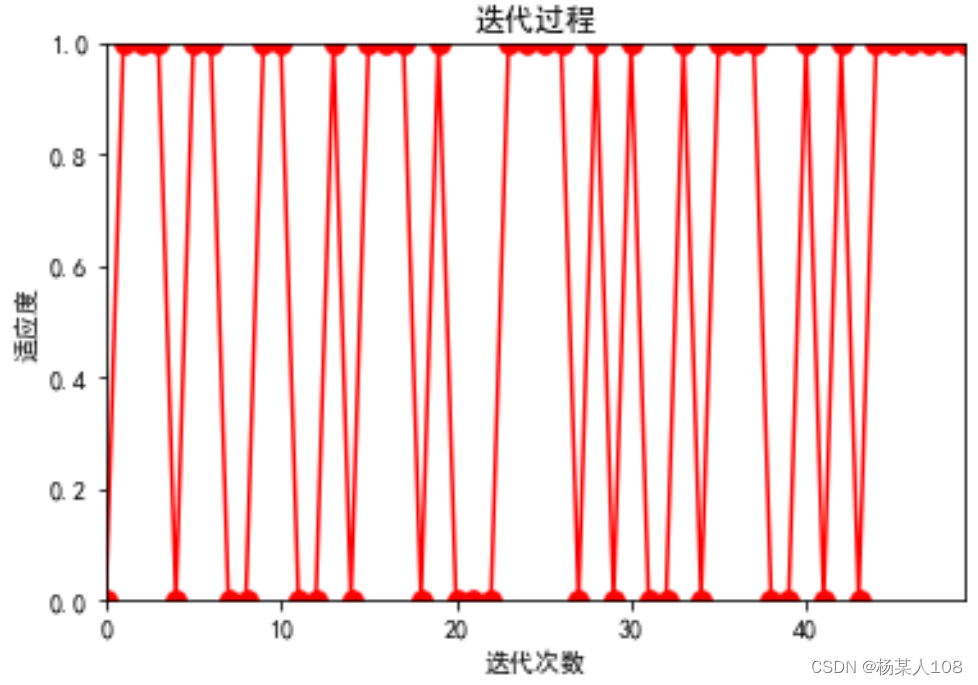
      n=15时

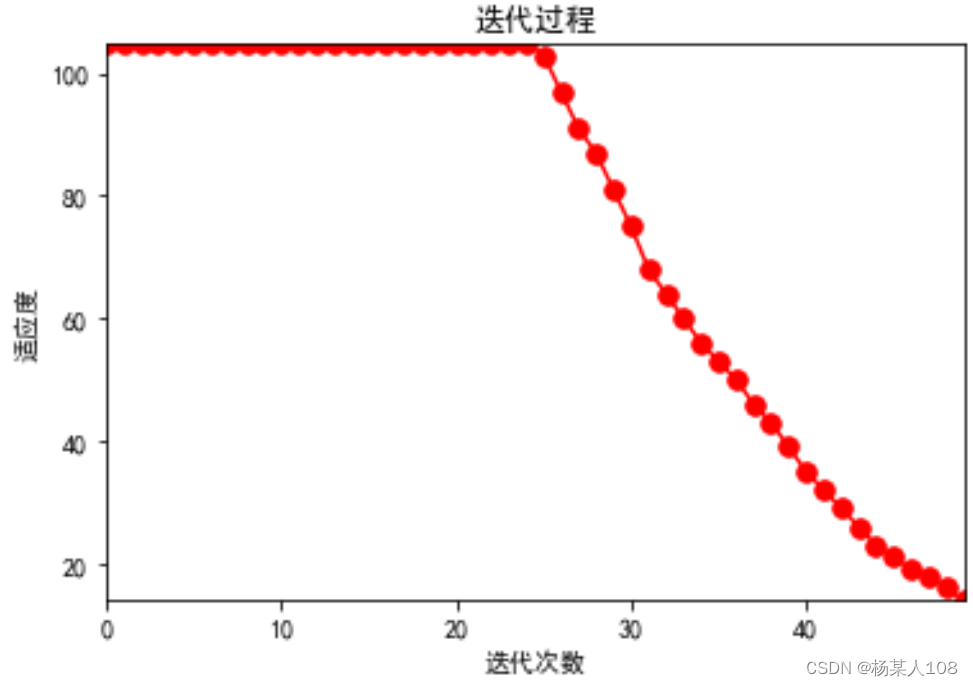
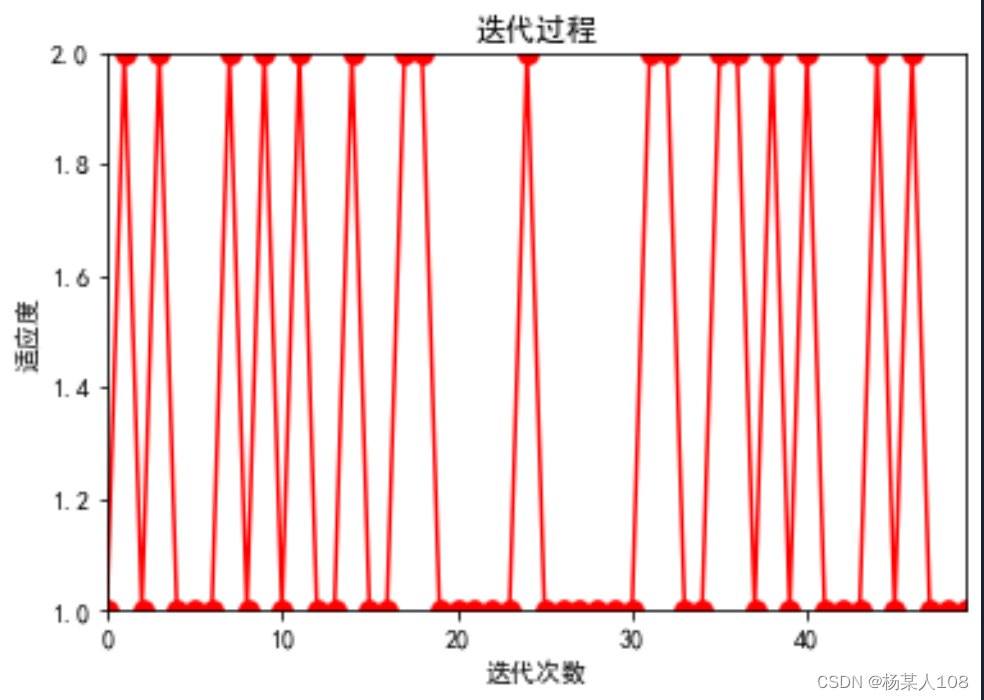
      n=20时

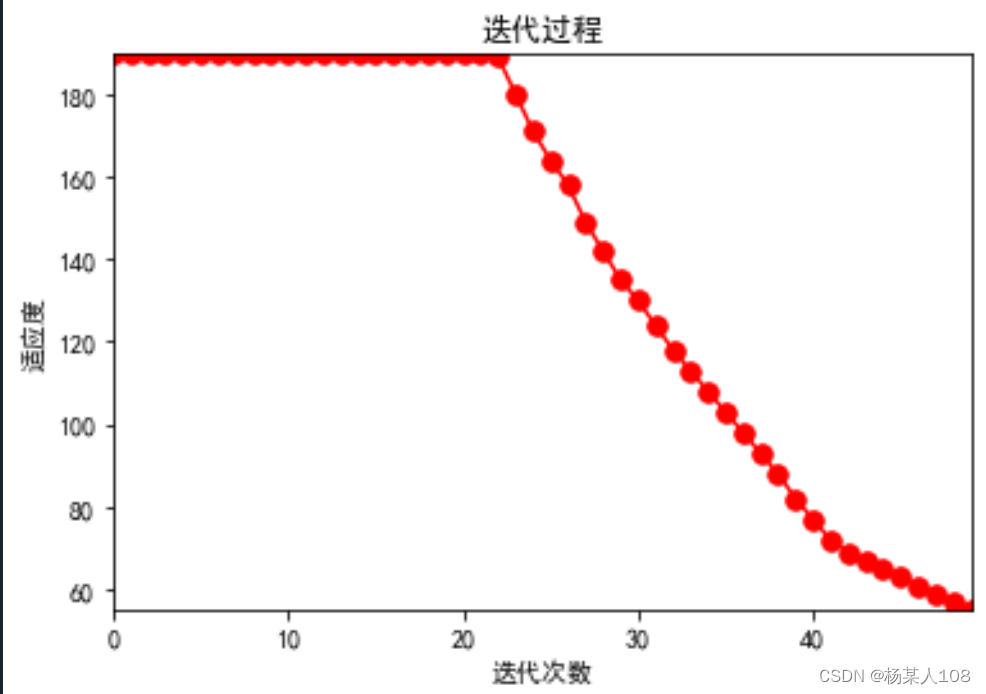
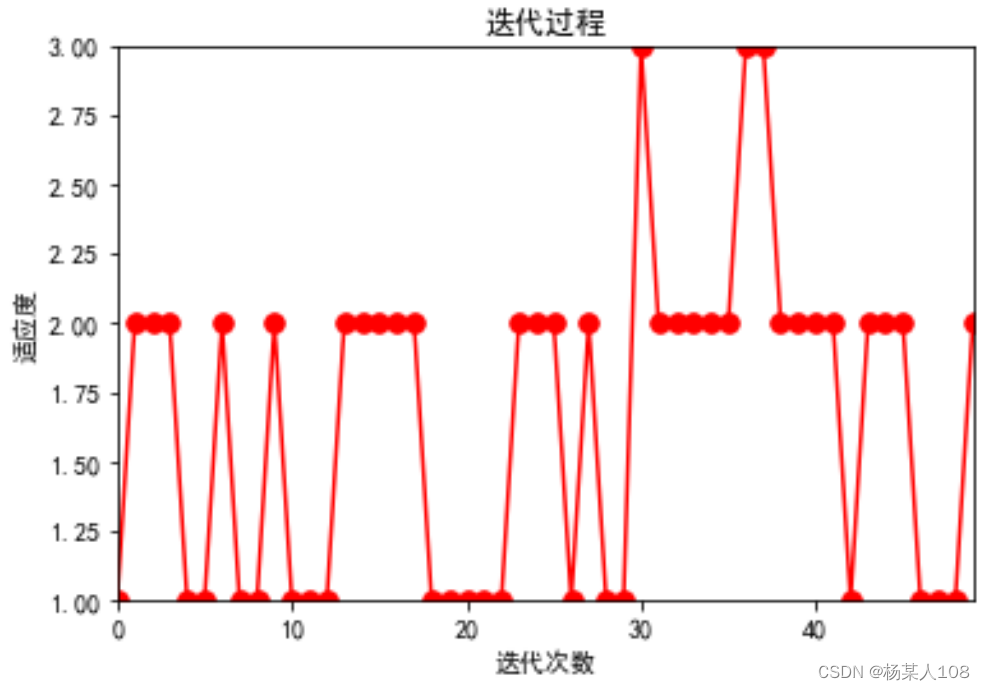
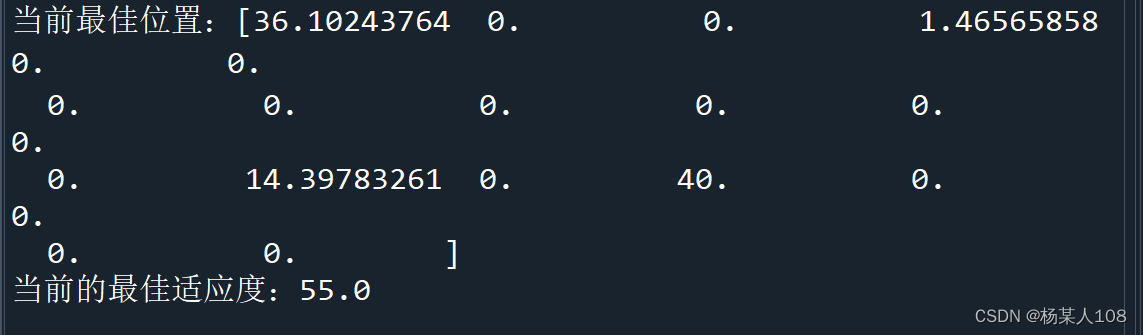
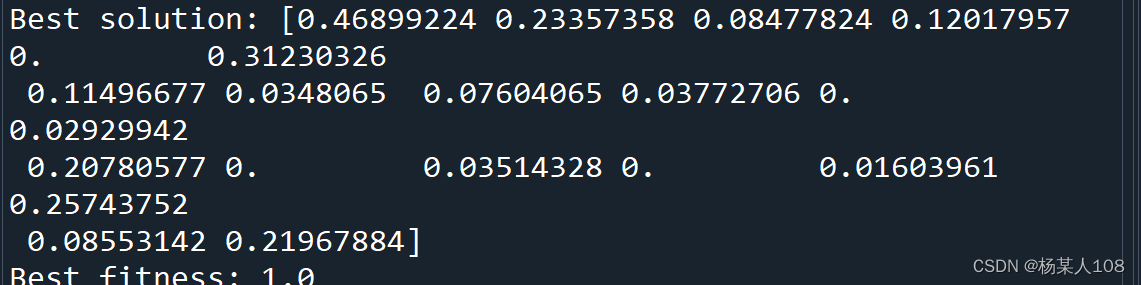
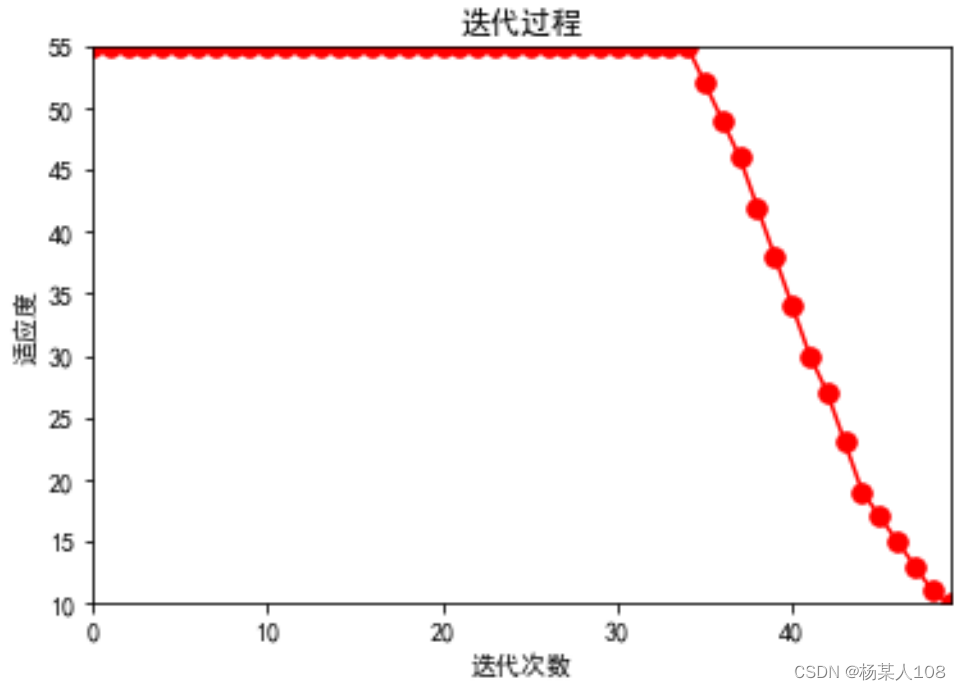
        这里发现在n=15时，两种算法均出现极值收敛错误，故分别取n=11、12、13、14多次实验，发现在n=11时粒子群算法多次出现极值收敛错误，蜂群算法并未出现错误。后续逐渐取大维数，发现在n=15时，蜂群算法开始出现极值收敛错误。

n=11

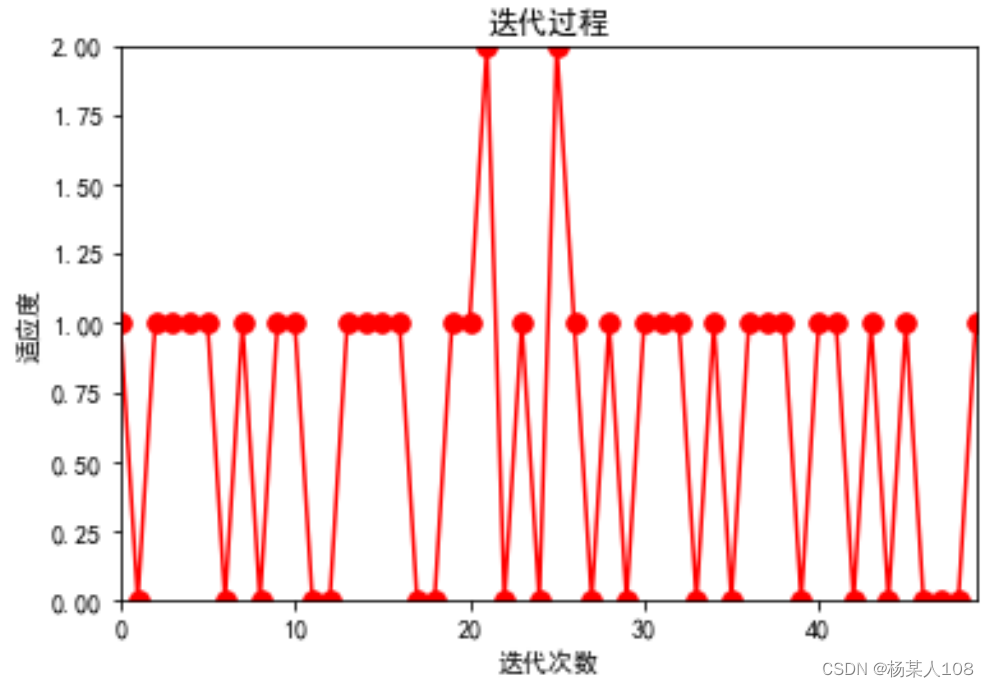
4. 对比结论

        由于粒子群算法和蜂群算法涉及参数较多，如粒子群算法涉及学习因子、惯性权重、粒子速度及方向等，蜂群算法涉及食物源、雇佣蜂、跟随蜂等，无法很好控制变量得出结论。但从多维函数极值对比可以得出初步结论：在维度n=11时,粒子群算法极值收敛位置出现问题，且收敛极值也出现错误。蜂群算法更加适用于多维度函数极值问题，蜂群算法适用于15维以内的极值问题。