＜＜数值分析＞＞第二章线性方程组的直接解法

解线性方程组是工程数学中最常见的模型之一。所说的“最常见”有两方面的含义：

１）一部分工程问题的本身建立的就是线性方程组模型；

２）较多工程问题建立的非线性方程组模型需要转化为线性方程组的求解。

线性方程组为Ax=b，x=以下介绍求解方法:

一.高斯列主元消去法

求解思路:把一般的线性方程组转换为梯形形式，再用每列最大数消去其他数。

1.1介绍

方程需要有唯一解，并且不接近不接近奇异矩阵。高斯列主元素消去法就是在消元的每一步选取（列）主元素——列中绝对值最大的元（数）取作主元素。在每轮消元前,根据需要消去的行，确定消元因子Lij（小于1的数）。以下是运算的步骤：

（1）选列主元素：从最左侧列开始选，同一列中最大值。 （2）交换两行：是列主元所在的行为第一行,若不是，则交换两行。 （3）消元运算：用列主元将每一列的其余项消为0。 （4）重复以上步骤 （5）代入求解：得到一个x的解，代入其他行，求解得到其他的x解。

1.2例题

用高斯列主元消去法解方程组：

解：

首先把方程组写成简化形式，再交换行，使首列从大到小排列，再用最大的数将其他的数化为0

易得方程组的解为

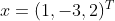
1.3特点

高斯列主元消去法是数值稳定的方法。

二.LU分解求解方程组

2.1公式介绍

高斯消去法的过程，可以看作下三角矩阵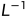左乘系数矩阵A ,乘积为可逆的上三角矩阵U。系数方程组为Ax=b,将Ux看作y，先解y，再解x。则有以下的公式：

 其中A为系数矩阵，L为单位的下三角矩阵，U为可逆的上三角矩阵

A=LU系数展开

2.2求解思路

（1）首先确定A分成的L和U。由 A 的第一行、第一列元素确定 U 的第一行、L 的第一列元素。再确定U的下一行，L的下一列。可以确定全部的L、U值。

（2）解方程组Ly=b，求解y的值，再解方程组Ux=y，求解x的值。

2.3例题

用LU分解，解方程组

线性方程组Ax=b

（1）对A进行LU分解：A=LU

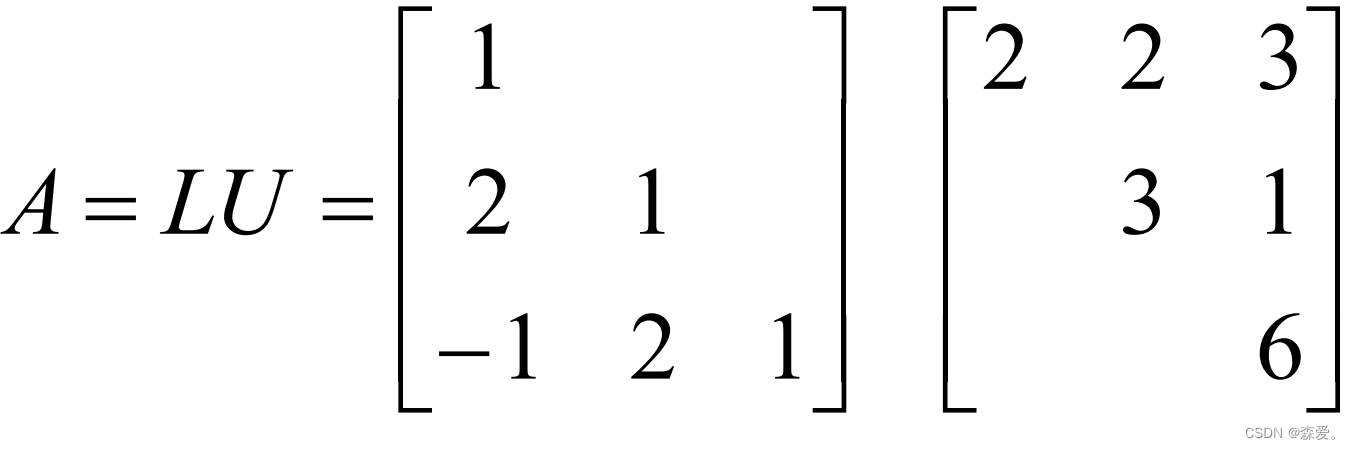
将系数矩阵A分解

易得y的解为

x的解为

三.特殊的LU分解

对称正定矩阵A的Cholesky的分解方法，和以A为系数矩阵的线性方程组的改进的平方根法。

3.1平方根法(Cholesky)

平方根法是解对称正定方程组的有效方法，系数矩阵A分解为L和U，再将U分解成D和Uo。可以得到A=L·D·Uo 。

(1)对称正定矩阵A有唯一的分解:

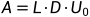，，且对称矩阵,则有，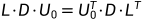

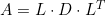
具体分解如下：

在A=LU分解的基础上，将U在分解成D和Uo。其中D是正定的对角矩阵,Uo为单位上三角矩阵。

(2)D是正定对角阵

其中D是正定对角阵——对角矩阵只在对角线上含有非0元素，其它位置都为0。

D的对角元素Uij。 记作:

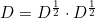
其中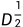为下图矩阵

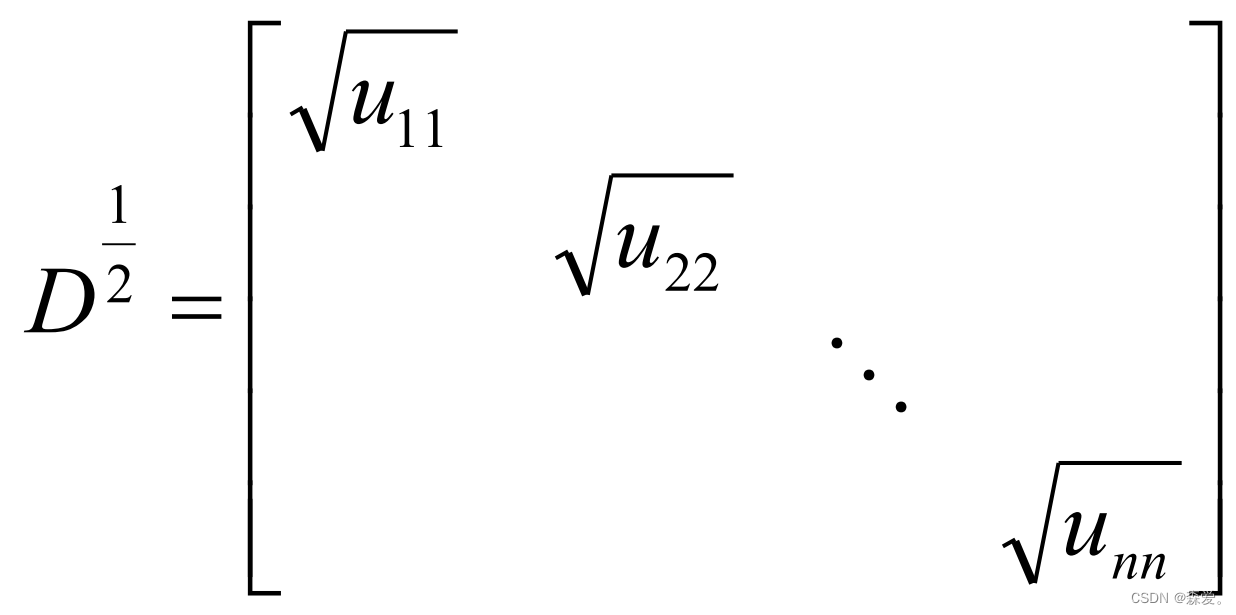
则A可以写作

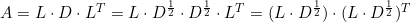
(3)Cholesky分解

将上述中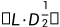记作L,则可以得到

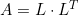
则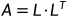被称为Cholesky分解。利用 Cholesky 直接分解公式，推导出的解方程组方法，称为 Cholesky 方法或平方根法。

(4)解方程组的平方根法(Cholesky)法

求解思路:

（1）首先将对称正定矩阵A分解成。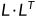

（2）根据矩阵乘法，逐步确定L的第i行元素，得到 。

（3）对于方程组 Ax=b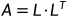，，得到,解Ly=b，得到y，在解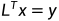，解得到x。

3.2改进的平方根法

3.2.1方法介绍

用平方根法解对称正定方程组时，求解L时用到开方的运算。为避免开方运算，改进平方根法，得到改进的平方根法——其适用于A是对称正定，或A对称且顺序主子式全不为0的情况。

将A分解为 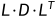，其中L是单位下三角矩阵，D是对角矩阵，分解的L、D如下 ：

求解思路

（1）首先将对称正定矩阵A分解为。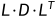

（2）解Ax=b， ，Ly=b首先解y，再解，解得y。

3.3例题：

3.3.1 用Cholesky 方法解方程组

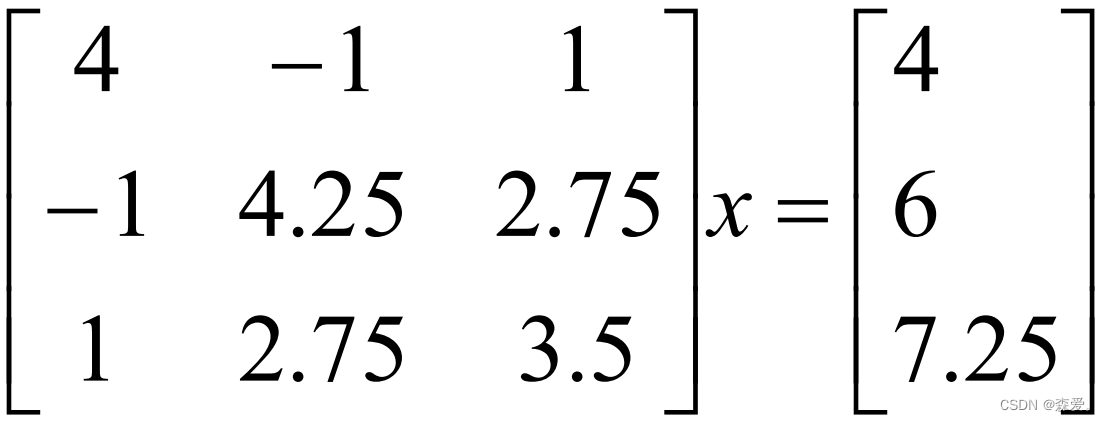
解：对系数矩阵A进行分解得到

解Ax=b，A=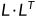,即，，先解Ly=b,得到y，再解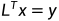，解得到x。

3.3.2 用改进的平方根方法解方程组

四.向量和矩阵的范数

为了对线性方程组的直接法做出误差分析，为了讨论方程组迭代法的收敛性。引入向量空间中向量及向量序列极限的大小。范数是用来度量向量和矩阵的大小的。

解向量位于n维空间的向量

1实数的绝对值: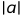是数轴上的点a到原点的距离。

2复数的模:=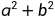，是平面上点(a，b)到原点(0，0)的距离。

4.1向量的范数

对于一个向量x，其满足条件，

（1）1—范数：取值为所有向量的绝对值之和。

向量方向相同

（2）2—范数：取值为向量和他的转置向量乘积，再开根号。

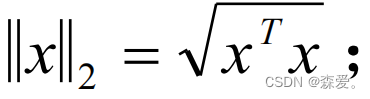
两个向量相垂直

（3）—范数：取值为向量中的最大值

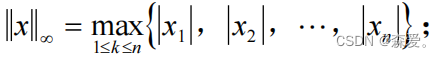
无穷向量取最大值

4.2矩阵的范数

（1）1—范数：取值为所有的列向量组中绝对值和最大值。

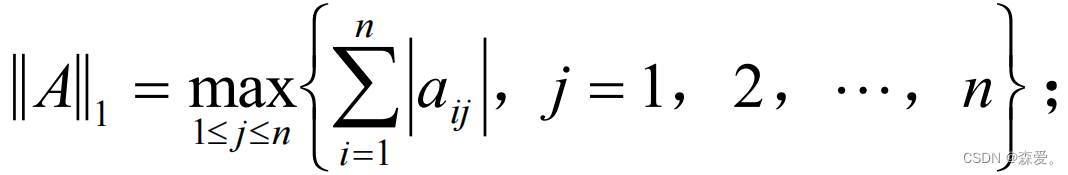
（2）2—范数：取值为A的转置和A的乘积的矩阵的最大的特征值，再开根号。

（3）—范数：取值为所有的行向量组中绝对值和的最大值。

（4）F—范数：取值为矩阵中所有值的平方和，再开根号。

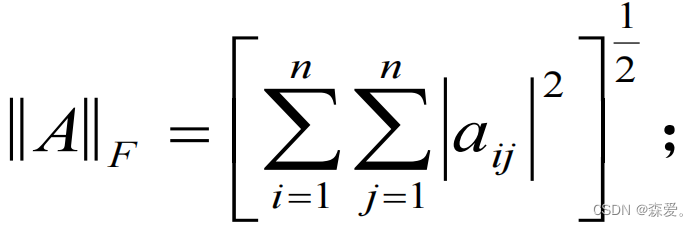
4.2.1 例题:

求矩阵的范数：

解得：

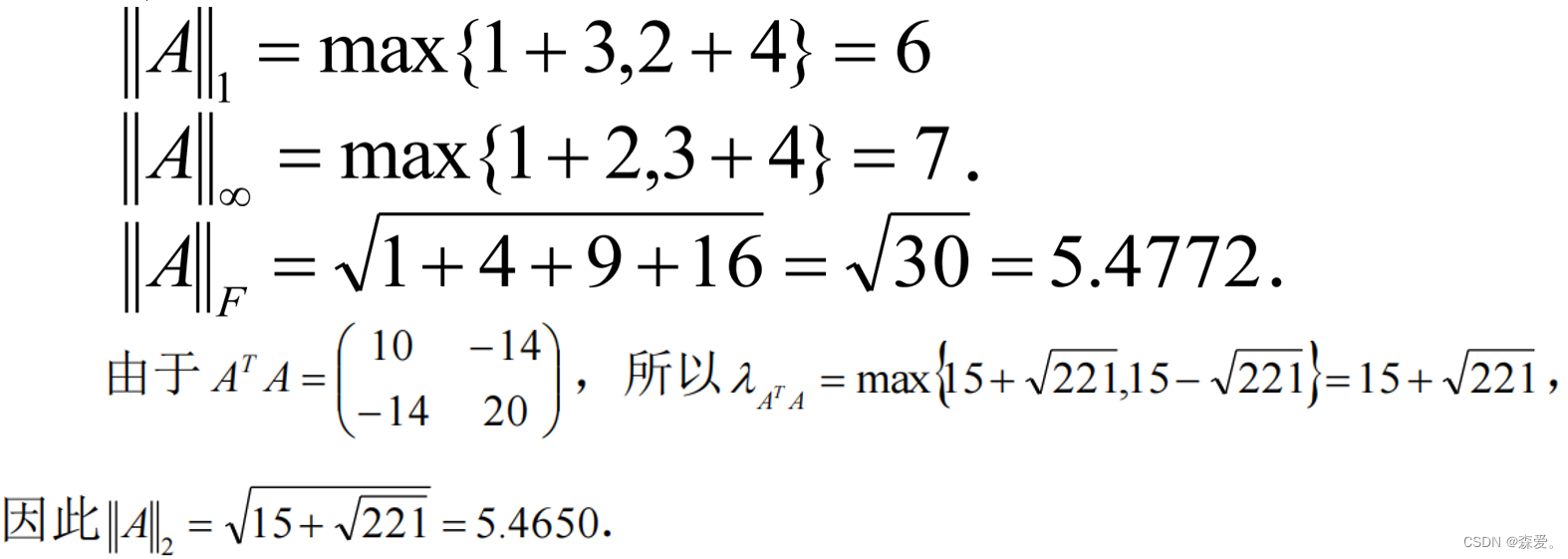
五.矩阵的条件数与直接法的误差分析

5.1误差原因

直接法解线性方程组产生误差的主要原因：

（1）算法的不同及舍入误差的影响。

（2）方程组固有的问题，本身存在病态——原始数据扰动对解影响。

5.1.1矩阵A和b扰动原因

矩阵A或常数项b存在观测误差和舍入误差，我们实际处理的可能是或者。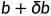

5.1.2病态矩阵介绍

如果矩阵A或者常数项b的微小变化，引起了方程组Ax=b的解——x的巨大变化，称此方程组为病态方程组，矩阵A相对于方程组为病态矩阵，反之称为良态方程组、良态矩阵。

5.1.3误差分析理论

刻划矩阵和方程组'病态'程度的标准——构建解的相对误差和系数矩阵A以及常数b的关系。

5.2线性方程组的误差分析

线性方程组为:Ax=b

其中，x和b，A为非奇异矩阵，x*为精确解，为解的误差，记作.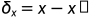

设为A的误差，为b的误差。

下面讨论与、的关系。

5.2.1 b有误差而A无误差的情形

将带有误差的右端项b和带误差的解向量x*代入方程组Ax=b，则有等式：

因为 x*为精确值，有A x*=b，同时消去，则有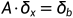，取范数，得不等式1

，

对Ax=b，取范数得不等式2

不等式1比不等式2可得

误差估计式：

其中方阵A的条件数 :

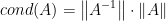
5.2.2条件数的性质

条件数很大的矩阵称为“病态”矩阵；病态矩阵对应的方程组称为病态方程组。反之，则称矩阵为良态矩阵，对应的方程组为良态方程组。

（1）解的相对误差是右端项b的相对误差的 cond(A)倍； （2）如果条件数越大，则解的相对误差就可能越大；

（3）条件数成了刻划矩阵的病态程度和方程组解对A或b扰动的敏感程度。

5.2.3A和b都有误差的情形

设方程组Ax=b0，A为非奇异矩阵，A和b都有误差，若A的误差非常小，使得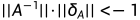，则有误差估计式:

5.2.3例题：

已知方程组Ax=b，b的扰动为，估计解的相对误差。

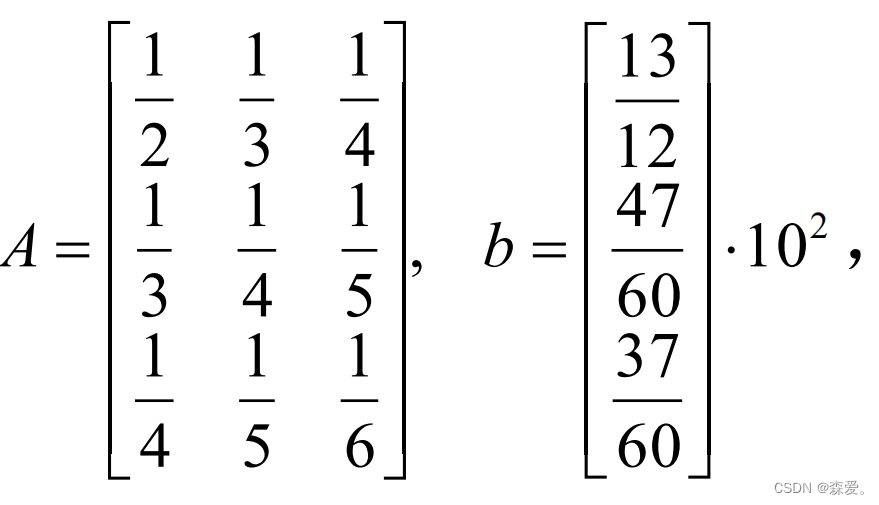
根据误差估计式：

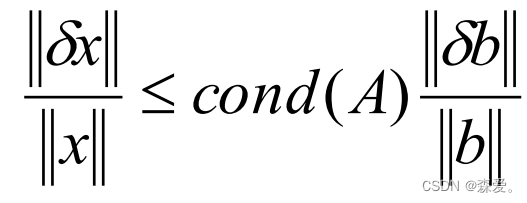
分别求解右侧的值cond(A)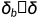，，并求解其无穷范数，代入不等式得 :

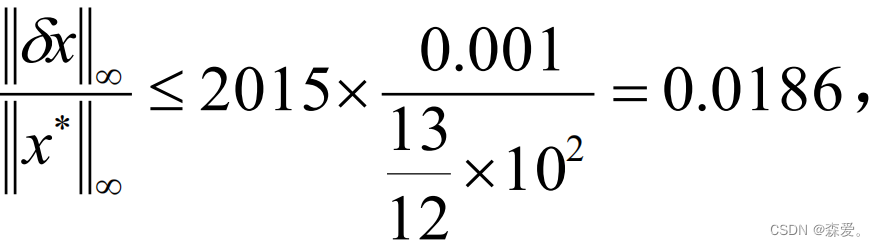
解的相对误差相比右端项b的相对误差相差了2015倍。

六.参考资料

1.<<数值分析>>北京理工大学出版，感谢曾繁慧 胡行华两位老师

2.辽宁工程技术大学，工程数学考试重点。

3.感谢鞠采洋对我的支持。

重点问题:

1方程组求解:使用高斯列主元消去法，(3阶以下方程)；

2方程组求解;使用LU分解求解方程组；

3特殊的LU分解:(Cholesky-平方根法)和(改进的平方根法);

4向量，矩阵，条件数，范数;

5直接法求解方程的误差分析。