【无标题】

奇异值分解(Singular Value Decomposition)是机器学习领域广泛应用的算法，可以用于降维，推荐系统，自然语言处理等领域。

          Ax=λx     （式-1）

A为n阶矩阵，x为非零向量，λ为常数，则称λ为A的特征值，x为A的特征向量

对于多个λ特征值，则有一个特征向量矩阵，得到如下公式

为特征向量矩阵，主对角线上为特征值，其余为0。

1. 右奇异矩阵V

      特征分解只能对方阵进行。对于非方阵的矩阵可以使用奇异值分解（SVD）。

        使用SVD，您可以将矩阵分解为三个矩阵。我们将这些新矩阵视为空间的子变换。不是在一个动作中进行转换，而是将其分解为三个动作。

        最后，我们会将SVD应用于图像处理，看到SVD对示例图像的影响。

        我们将A分解为3个矩阵（而不是使用特征分解的两个）：

奇异值分解 (SVD)
         矩阵 U、D 和 V 具有以下属性：

        U和V是正交矩阵并且

        D是一个对角矩阵（除对角线外全为 0）。 然而D不一定是正方形的。 

        U称为A的左奇异向量，而V称为A的右奇异向量。沿D对角线的值是A的奇异值。

        以下是分解的维度：

奇异值分解的维度
         奇异值的对角矩阵不是正方形，而是具有 A 的形状。

        下面是Numpy文档中提供的示例，创建了一个与 A 形状相同的零矩阵并用奇异值填充它：

smat = np.zeros((9, 6), dtype=complex)
smat[:6, :6] = np.diag(s)
        对于奇异值分解背后的直觉需要对矩阵变换的思想进行一些解释。这里有几个示例展示了如何通过 2D 方阵转换空间。 希望可以更好地理解：A 是一个矩阵，可以看作是一个线性变换。 该变换可以分解为三个子变换：1. 旋转，2. 重新缩放，3. 旋转。 这三个步骤对应于三个矩阵 U、D 和 V。
 

2.　对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：

　　　　其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵

来表示。

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）

3.行降维和列将维

本节通过协方差的角度去理解行降维和列降维，首先探讨下协方差的含义：

单个变量用方差描述，无偏方差公式：

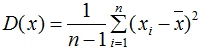
两个变量用协方差描述，协方差公式：

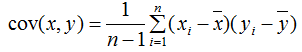
多个变量（如三个变量）之间的关系可以用协方差矩阵描述：

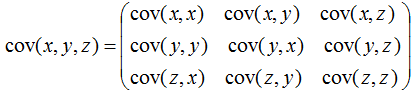
相关系数公式：

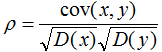
由上式可知，协方差是描述变量间的相关关系程度：

1）协方差cov(x,y) > 0时，变量x与y正相关；

2）协方差cov(x,y)<0时，变量x与y负相关；

3）协方差cov(x,y)=0时，变量x与y不相关；

 

4.任何矩阵都能进行SVD分解，SVD可以用于行降维和列降维，SVD在数据压缩、推荐系统和语义分析有广泛的应用，SVD与PCA的缺点一样，分解出的矩阵解释性不强 .