文章目录
三角函数常用公式的证明
只需证明和差公式即可证明其它公式。
和差公式几何证明
此处我们用几何来证明:
如图所示,矩形BEDF中存在一斜边长度为1的直角三角形 △ A C B \triangle ACB △ACB ,求证: sin ( α + β ) = sin α cos β + cos α sin β , sin ( γ − β ) = sin γ cos β − cos γ sin β \sin{(\alpha+\beta)} = \sin{\alpha} \cos{\beta} + \cos{\alpha}\sin{\beta}, \sin{(\gamma-\beta)} = \sin{\gamma}\cos{\beta} - \cos{\gamma}\sin{\beta} sin(α+β)=sinαcosβ+cosαsinβ,sin(γ−β)=sinγcosβ−cosγsinβ。

解:易得 α + β = ∠ E B A = ∠ F A B \alpha + \beta = \angle EBA = \angle FAB α+β=∠EBA=∠FAB,将BF平移至A点,有 B F = sin ( α + β ) , A F = cos ( α + β ) BF = \sin{(\alpha+\beta)}\,,AF=\cos{(\alpha+\beta)} BF=sin(α+β),AF=cos(α+β),
其中 B F = E C + C D = B C sin ∠ E B C + A C cos ∠ D C A BF = EC + CD = BC \sin{\angle EBC} + AC \cos{\angle DCA} BF=EC+CD=BCsin∠EBC+ACcos∠DCA,
A F = D F − D A = E B − D A = B C cos ∠ E B C − A C sin ∠ D C A AF = DF - DA = EB - DA = BC \cos{\angle EBC} - AC \sin{\angle DCA} AF=DF−DA=EB−DA=BCcos∠EBC−ACsin∠DCA,
又 ∠ E B C + ∠ B C E = ∠ B C E + ∠ D C A = π 2 \angle EBC + \angle BCE = \angle BCE + \angle DCA = \frac \pi 2 ∠EBC+∠BCE=∠BCE+∠DCA=2π, B C = cos β BC = \cos{\beta} BC=cosβ, A C = sin β AC = \sin{\beta} AC=sinβ,
故
sin
(
α
+
β
)
=
sin
α
cos
β
+
cos
α
sin
β
\sin{(\alpha+\beta)} =\sin{\alpha}\cos{\beta} +\cos{\alpha}\sin{\beta}
sin(α+β)=sinαcosβ+cosαsinβ,
cos ( α + β ) = cos α cos β − sin α sin β \cos{(\alpha+\beta)} = \cos{\alpha} \cos{\beta}-\sin{\alpha}\sin{\beta} cos(α+β)=cosαcosβ−sinαsinβ, 两式相除得 tan ( α + β ) = t a n α + t a n β 1 − tan α tan β \tan{(\alpha+\beta)} = \frac {tan{\alpha + tan{\beta}}}{1-\tan{\alpha}\tan{\beta}} tan(α+β)=1−tanαtanβtanα+tanβ 。
对于 sin ( γ − β ) \sin{(\gamma-\beta)} sin(γ−β) ,方法类似,当然也可以通过 γ = π 2 − α \gamma = \frac \pi 2 - \alpha γ=2π−α 和诱导公式来做:
sin ( γ − β ) = cos ( α + β ) = cos α cos β − sin α sin β = sin γ cos β − cos γ sin β \sin{(\gamma - \beta)} = \cos{(\alpha+\beta)}=\cos{\alpha} \cos{\beta} - \sin{\alpha}\sin{\beta}=\sin{\gamma} \cos{\beta} - \cos{\gamma}\sin{\beta} sin(γ−β)=cos(α+β)=cosαcosβ−sinαsinβ=sinγcosβ−cosγsinβ ,
cos ( γ − β ) = sin ( α + β ) = sin α cos β + cos α sin β = cos γ cos β + sin γ sin β \cos{(\gamma - \beta)} = \sin{(\alpha+\beta)}=\sin{\alpha} \cos{\beta} + \cos{\alpha}\sin{\beta}=\cos{\gamma} \cos{\beta} + \sin{\gamma}\sin{\beta} cos(γ−β)=sin(α+β)=sinαcosβ+cosαsinβ=cosγcosβ+sinγsinβ ,
tan ( γ − β ) = t a n γ − t a n β 1 + tan γ tan β \tan{(\gamma-\beta)} = \frac {tan{\gamma - tan{\beta}}}{1+\tan{\gamma}\tan{\beta}} tan(γ−β)=1+tanγtanβtanγ−tanβ
和差公式的欧拉证明:
用欧拉公式证明三角函数和差公式的核心在于利用指数函数与三角函数的关系,将复数乘法转化为三角函数运算。以下是具体证明过程:
欧拉公式为: e i θ = cos θ + i sin θ e^{i\theta} = \cos\theta + i\sin\theta eiθ=cosθ+isinθ ,其共轭形式为: e − i θ = cos θ − i sin θ e^{-i\theta} = \cos\theta - i\sin\theta e−iθ=cosθ−isinθ
1. cos ( a + b ) \cos(a + b) cos(a+b) 和 sin ( a + b ) \sin(a + b) sin(a+b)
考虑 e i ( a + b ) e^{i(a + b)} ei(a+b),根据指数运算性质: e i ( a + b ) = e i a ⋅ e i b e^{i(a + b)} = e^{ia} \cdot e^{ib} ei(a+b)=eia⋅eib 将右边展开为复数乘积:
( cos a + i sin a ) ( cos b + i sin b ) = cos a cos b + i cos a sin b + i sin a cos b + i 2 sin a sin b (\cos a + i\sin a)(\cos b + i\sin b) = \cos a\cos b + i\cos a\sin b + i\sin a\cos b + i^2\sin a\sin b (cosa+isina)(cosb+isinb)=cosacosb+icosasinb+isinacosb+i2sinasinb
由于 i 2 = − 1 i^2 = -1 i2=−1,化简后得到: cos a cos b − sin a sin b + i ( cos a sin b + sin a cos b ) \cos a\cos b - \sin a\sin b + i(\cos a\sin b + \sin a\cos b) cosacosb−sinasinb+i(cosasinb+sinacosb)
而左边根据欧拉公式为: e i ( a + b ) = cos ( a + b ) + i sin ( a + b ) e^{i(a + b)} = \cos(a + b) + i\sin(a + b) ei(a+b)=cos(a+b)+isin(a+b) 比较实部和虚部,得: { cos ( a + b ) = cos a cos b − sin a sin b sin ( a + b ) = sin a cos b + cos a sin b \begin{cases} \cos(a + b) = \cos a\cos b - \sin a\sin b \\ \sin(a + b) = \sin a\cos b + \cos a\sin b \end{cases} {cos(a+b)=cosacosb−sinasinbsin(a+b)=sinacosb+cosasinb
2. cos ( a − b ) \cos(a - b) cos(a−b) 和 sin ( a − b ) \sin(a - b) sin(a−b)
类似地,考虑 e i ( a − b ) e^{i(a - b)} ei(a−b): e i ( a − b ) = e i a ⋅ e − i b e^{i(a - b)} = e^{ia} \cdot e^{-ib} ei(a−b)=eia⋅e−ib 展开右边:
( cos a + i sin a ) ( cos b − i sin b ) = cos a cos b − i cos a sin b + i sin a cos b − i 2 sin a sin b (\cos a + i\sin a)(\cos b - i\sin b) = \cos a\cos b - i\cos a\sin b + i\sin a\cos b - i^2\sin a\sin b (cosa+isina)(cosb−isinb)=cosacosb−icosasinb+isinacosb−i2sinasinb
化简后: cos a cos b + sin a sin b + i ( sin a cos b − cos a sin b ) \cos a\cos b + \sin a\sin b + i(\sin a\cos b - \cos a\sin b) cosacosb+sinasinb+i(sinacosb−cosasinb)
左边根据欧拉公式为: e i ( a − b ) = cos ( a − b ) + i sin ( a − b ) e^{i(a - b)} = \cos(a - b) + i\sin(a - b) ei(a−b)=cos(a−b)+isin(a−b) 比较实部和虚部,得: { cos ( a − b ) = cos a cos b + sin a sin b sin ( a − b ) = sin a cos b − cos a sin b \begin{cases} \cos(a - b) = \cos a\cos b + \sin a\sin b \\ \sin(a - b) = \sin a\cos b - \cos a\sin b \end{cases} {cos(a−b)=cosacosb+sinasinbsin(a−b)=sinacosb−cosasinb
口诀辅助记忆:
- 正弦和差:乘积符号相同( sin ( a ± b ) = sin a cos b ± cos a sin b \sin(a \pm b) = \sin a\cos b \pm \cos a\sin b sin(a±b)=sinacosb±cosasinb),谐音为:帅哥很帅符号同。
- 余弦和差:乘积符号相反( cos ( a ± b ) = cos a cos b ∓ sin a sin b \cos(a \pm b) = \cos a\cos b \mp \sin a\sin b cos(a±b)=cosacosb∓sinasinb),谐音为:哥哥帅帅符号异。
其它三角函数公式的证明
诱导公式可由和差公式推导,此处不再赘述。
结合 sin 2 α + cos 2 α = 1 \sin^2{\alpha} + \cos^2{\alpha} = 1 sin2α+cos2α=1,在和差公式中,当 α \alpha α 与 β \beta β 相等时可以推导出倍角公式。
将倍角公式中的 α \alpha α 换成 α 2 \frac\alpha 2 2α 就可推导出降幂公式,两边同时开根号就变成了半角公式。
由半角公式又可推导出万能公式。
和差化积公式就是通过 α = α + β 2 + α − β 2 \alpha = \frac{\alpha + \beta}2 + \frac{\alpha-\beta}2 α=2α+β+2α−β 和 β = α + β 2 − α − β 2 \beta = \frac{\alpha + \beta}2 - \frac{\alpha-\beta}2 β=2α+β−2α−β 结合和差公式推导的,其逆过程就是积化和差公式。
比如,
sin
α
+
sin
β
=
sin
(
α
+
β
2
+
α
−
β
2
)
+
sin
(
α
+
β
2
−
α
−
β
2
)
=
2
sin
α
+
β
2
cos
α
−
β
2
\sin{\alpha}+\sin{\beta} = \sin{( \frac{\alpha + \beta}2 + \frac{\alpha-\beta}2)}+\sin{( \frac{\alpha + \beta}2 - \frac{\alpha-\beta}2)}=2\sin{\frac{\alpha+\beta}2}\cos{\frac{\alpha-\beta}2}
sinα+sinβ=sin(2α+β+2α−β)+sin(2α+β−2α−β)=2sin2α+βcos2α−β,
令
c
=
α
+
β
2
c=\frac{\alpha + \beta}2
c=2α+β,
b
=
α
−
β
2
b = \frac{\alpha-\beta}2
b=2α−β ,
解得
α
=
c
+
b
\alpha = c + b
α=c+b,
β
=
c
−
b
\beta = c - b
β=c−b,
代入上式得 sin c cos b = 1 2 [ sin ( c + b ) + sin ( c − b ) ] \sin{c}\cos{b}=\frac 1 2 [\sin{(c+b)}+\sin{(c-b)}] sinccosb=21[sin(c+b)+sin(c−b)] 。
1 + tan 2 α = sec 2 α 1 + \tan^2{\alpha} = \sec^2{\alpha} 1+tan2α=sec2α 与 1 + cot 2 α = csc 2 α 1 + \cot^2{\alpha} = \csc^2{\alpha} 1+cot2α=csc2α是通过 sin 2 α + cos 2 α = 1 \sin^2{\alpha} + \cos^2{\alpha} = 1 sin2α+cos2α=1 、 sec α = 1 cos α \sec{\alpha} = \frac 1 {\cos{\alpha}} secα=cosα1 和 csc α = 1 sin α \csc{\alpha}=\frac 1 {\sin{\alpha}} cscα=sinα1 来证明的。
反三角函数常见公式的证明
反函数的重要性质:
f ( f − 1 ( x ) ) = x 对 f − 1 ( x ) 的定义域有效 f(f^{-1}(x)) = x 对f^{-1}(x)的定义域有效 f(f−1(x))=x对f−1(x)的定义域有效
f − 1 ( f ( x ) ) = x 对 f ( x ) 的定义域有效 f^{-1}(f(x)) = x 对f(x)的定义域有效 f−1(f(x))=x对f(x)的定义域有效
反三角函数的公式是通过反函数的定义与性质,结合三角函数的恒等式、导数规则及几何意义推导而来的,但需严格考虑定义域和主值范围的限制。
一、基础恒等式(互为反函数)
-
反正弦与正弦
sin ( arcsin x ) = x ( x ∈ [ − 1 , 1 ] ) \sin(\arcsin x) = x \quad (x \in [-1, 1]) sin(arcsinx)=x(x∈[−1,1])
arcsin ( sin x ) = x ( x ∈ [ − π / 2 , π / 2 ] ) \arcsin(\sin x) = x \quad (x \in [-\pi/2, \pi/2]) arcsin(sinx)=x(x∈[−π/2,π/2]) -
反余弦与余弦
cos ( arccos x ) = x ( x ∈ [ − 1 , 1 ] ) \cos(\arccos x) = x \quad (x \in [-1, 1]) cos(arccosx)=x(x∈[−1,1])
arccos ( cos x ) = x ( x ∈ [ 0 , π ] ) \arccos(\cos x) = x \quad (x \in [0, \pi]) arccos(cosx)=x(x∈[0,π]) -
反正切与正切
tan ( arctan x ) = x ( x ∈ R ) \tan(\arctan x) = x \quad (x \in \mathbb{R}) tan(arctanx)=x(x∈R)
arctan ( tan x ) = x ( x ∈ ( − π / 2 , π / 2 ) ) \arctan(\tan x) = x \quad (x \in (-\pi/2, \pi/2)) arctan(tanx)=x(x∈(−π/2,π/2))
二、角度和与差恒等式
-
互余关系
- arcsin x + arccos x = π 2 ( x ∈ [ − 1 , 1 ] ) \arcsin x + \arccos x = \frac{\pi}{2} \quad (x \in [-1, 1]) arcsinx+arccosx=2π(x∈[−1,1])
- arctan x + arccot x = π 2 ( x ∈ R ) \arctan x + \text{arccot} \, x = \frac{\pi}{2} \quad (x \in \mathbb{R}) arctanx+arccotx=2π(x∈R)
口诀:互余角,相加 π/2。
证:设 θ = arcsin x \theta = \arcsin x θ=arcsinx,其中 x ∈ [ − 1 , 1 ] x \in [-1, 1] x∈[−1,1]。根据定义: sin θ = x 且 θ ∈ [ − π 2 , π 2 ] \sin\theta = x \quad \text{且} \quad \theta \in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right] sinθ=x且θ∈[−2π,2π]
由三角恒等式 sin θ = cos ( π 2 − θ ) \sin\theta = \cos\left(\frac{\pi}{2} - \theta\right) sinθ=cos(2π−θ),得: x = cos ( π 2 − θ ) x = \cos\left(\frac{\pi}{2} - \theta\right) x=cos(2π−θ)
由于 π 2 − θ ∈ [ 0 , π ] \frac{\pi}{2} - \theta \in [0, \pi] 2π−θ∈[0,π](反余弦函数的定义域),根据反余弦定义: arccos x = π 2 − θ \arccos x = \frac{\pi}{2} - \theta arccosx=2π−θ
合并表达式 arcsin x + arccos x = θ + ( π 2 − θ ) = π 2 \arcsin x + \arccos x = \theta + \left(\frac{\pi}{2} - \theta\right) = \frac{\pi}{2} arcsinx+arccosx=θ+(2π−θ)=2π
PS:在这里提一嘴, sin ( arccos x ) \sin(\arccos x) sin(arccosx)你可以通过上式转换成 sin ( π − arcsin x ) \sin(\pi-\arcsin x) sin(π−arcsinx)。
- 和角公式
-
arcsin a + arcsin b = arcsin ( a 1 − b 2 + b 1 − a 2 ) 当 a , b ≥ 0 且 a 2 + b 2 ≤ 1 时 \arcsin a + \arcsin b = \arcsin\left(a\sqrt{1-b^2} + b\sqrt{1-a^2}\right)\\当 a, b \geq 0 且 a^2 + b^2 \leq 1 时 arcsina+arcsinb=arcsin(a1−b2+b1−a2)当a,b≥0且a2+b2≤1时
证:令 a = s i n A a=sinA a=sinA, b = s i n B b=sinB b=sinB
则原等式右边为 a r c s i n ( s i n A c o s B + c o s A s i n B ) = a r c s i n ( s i n ( A + B ) ) = A + B arcsin(sinAcosB+cosAsinB)=arcsin(sin(A+B))=A+B arcsin(sinAcosB+cosAsinB)=arcsin(sin(A+B))=A+B
而当满足条件时时,上式即等于原等式左边.
-
arctan a + arctan b = arctan ( a + b 1 − a b ) (当 a b < 1 时) \arctan a + \arctan b = \arctan\left(\frac{a + b}{1 - ab}\right) \quad \text{(当 } ab < 1 \text{ 时)} arctana+arctanb=arctan(1−aba+b)(当 ab<1 时)
三、与原三角函数的关系
-
反余弦的正弦表达式
sin ( arccos x ) = 1 − x 2 ( x ∈ [ − 1 , 1 ] ) \sin(\arccos x) = \sqrt{1 - x^2} \quad (x \in [-1, 1]) sin(arccosx)=1−x2(x∈[−1,1])
证:令 t = arccos x ∈ [ 0 , π ] t=\arccos{x}\in[0,\pi] t=arccosx∈[0,π] ,则 x = cos t x=\cos{t} x=cost , sin t ≥ 0 \sin{t} \geq 0 sint≥0 ,
又 sin 2 α + cos 2 α = 1 \sin^2{\alpha} + \cos^2{\alpha} = 1 sin2α+cos2α=1 ,因此 sin t = 1 − x 2 \sin{t} = \sqrt{1-x^2} sint=1−x2,即 sin ( arccos x ) = 1 − x 2 ( x ∈ [ − 1 , 1 ] ) \sin(\arccos x) = \sqrt{1 - x^2} \quad (x \in [-1, 1]) sin(arccosx)=1−x2(x∈[−1,1])
-
反正弦的余弦表达式
cos ( arcsin x ) = 1 − x 2 ( x ∈ [ − 1 , 1 ] ) \cos(\arcsin x) = \sqrt{1 - x^2} \quad (x \in [-1, 1]) cos(arcsinx)=1−x2(x∈[−1,1])
-
反正切的正弦与余弦
sin ( arctan x ) = x 1 + x 2 \sin(\arctan x) = \frac{x}{\sqrt{1 + x^2}} sin(arctanx)=1+x2x,
cos ( arctan x ) = 1 1 + x 2 \quad \cos(\arctan x) = \frac{1}{\sqrt{1 + x^2}} cos(arctanx)=1+x21证:设 θ = arctan x \theta = \arctan x θ=arctanx,其中 x ∈ R x \in \mathbb{R} x∈R。根据定义:
tan θ = x 且 θ ∈ ( − π 2 , π 2 ) \tan\theta = x \quad \text{且} \quad \theta \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) tanθ=x且θ∈(−2π,2π)
由 1 + tan 2 θ = sec 2 θ 1 + \tan^2\theta = \sec^2\theta 1+tan2θ=sec2θ,代入 tan θ = x \tan\theta = x tanθ=x:
1 + x 2 = sec 2 θ ⟹ cos θ = 1 sec θ = 1 1 + x 2 1 + x^2 = \sec^2\theta \implies \cos\theta = \frac{1}{\sec\theta} = \frac{1}{\sqrt{1 + x^2}} 1+x2=sec2θ⟹cosθ=secθ1=1+x21
由 sin θ = tan θ ⋅ cos θ \sin\theta = \tan\theta \cdot \cos\theta sinθ=tanθ⋅cosθ,代入 tan θ = x \tan\theta = x tanθ=x 和 cos θ = 1 1 + x 2 \cos\theta = \frac{1}{\sqrt{1 + x^2}} cosθ=1+x21:
sin θ = x ⋅ 1 1 + x 2 = x 1 + x 2 \sin\theta = x \cdot \frac{1}{\sqrt{1 + x^2}} = \frac{x}{\sqrt{1 + x^2}} sinθ=x⋅1+x21=1+x2x
四、反函数间的转换
-
反余弦与反正弦
arccos x = arcsin ( 1 − x 2 ) ( x ∈ [ 0 , 1 ] ) \arccos x = \arcsin\left(\sqrt{1 - x^2}\right) \quad (x \in [0, 1]) arccosx=arcsin(1−x2)(x∈[0,1])
证:该式其实就是通过反余弦的正弦表达式转换过来的。
-
反余切与反正切
arccot x = arctan ( 1 x ) ( x > 0 ) \text{arccot} \, x = \arctan\left(\frac{1}{x}\right) \quad (x > 0) arccotx=arctan(x1)(x>0)
总结
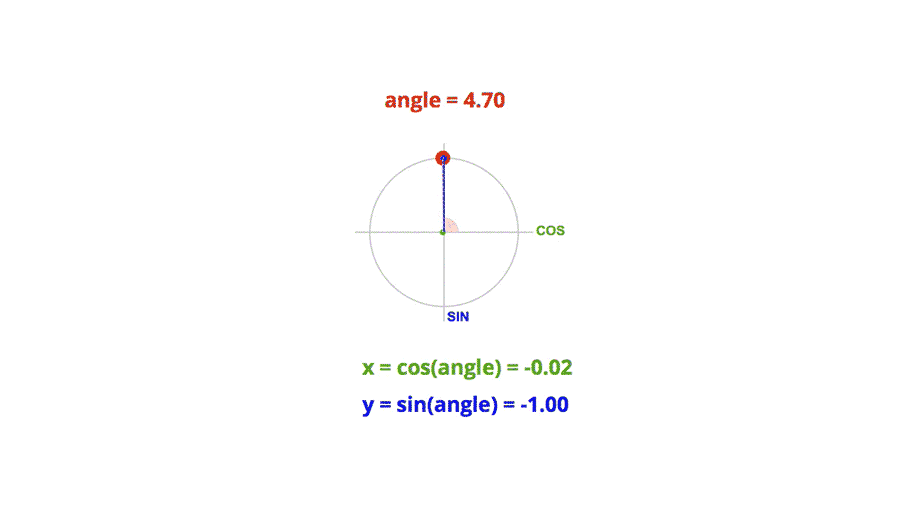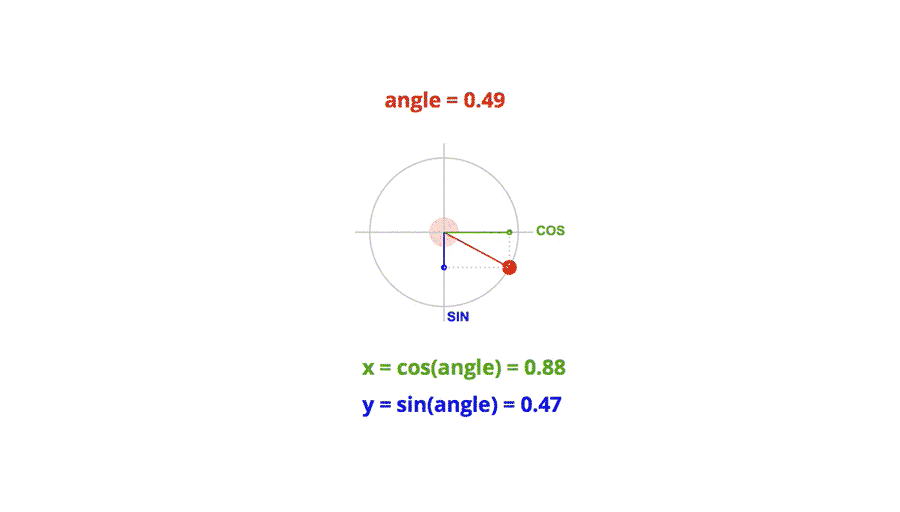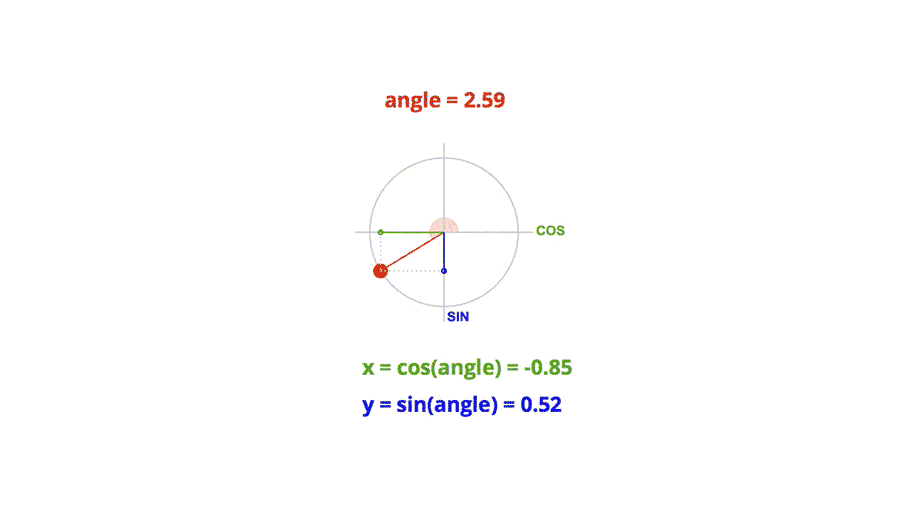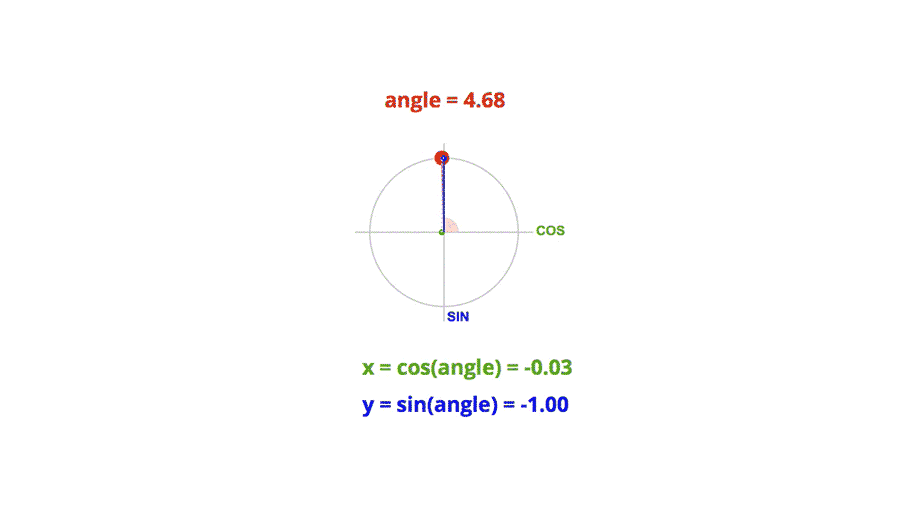
三角函数是单位圆中给定圆心角求坐标分量;反三角函数是给定坐标分量求主值范围内的圆心角。
具体解释:
-
三角函数:在单位圆中,给定一个圆心角 θ \theta θ,单位圆上对应的点的坐标为 ( cos θ , sin θ ) (\cos\theta, \sin\theta) (cosθ,sinθ),其中 cos θ \cos\theta cosθ 和 sin θ \sin\theta sinθ 分别是该圆心角的横坐标和纵坐标。因此,三角函数就是通过给定圆心角 θ \theta θ,来求出对应的坐标分量(即 cos θ \cos\theta cosθ 和 sin θ \sin\theta sinθ)。
-
反三角函数:反三角函数的作用是,给定单位圆上一个点的坐标(通常是 cos θ \cos\theta cosθ 和 sin θ \sin\theta sinθ),求出对应的圆心角 θ \theta θ,而且反三角函数通常会限定在主值范围内(例如, arcsin \arcsin arcsin 的主值范围是 [ − π 2 , π 2 ] [- \frac{\pi}{2}, \frac{\pi}{2}] [−2π,2π], arccos \arccos arccos 的主值范围是 [ 0 , π ] [0, \pi] [0,π])。因此,反三角函数的作用是根据给定的坐标分量,求出对应的圆心角。
总结:三角函数是从圆心角到坐标分量的映射,反三角函数则是从坐标分量到圆心角的映射,通常会有主值范围的限制。
PS:我为什么不全部证明呢?
子曰:不愤不启,不悱不发,举一隅不以三隅反,则不复也。
译文:教导学生,不到他冥思苦想仍不得其解的时候,不去开导他,不到他想说却说不出来的时候,不去启发他。给他指出一个方面,如果他不能由此推知其他三个方面,就不再重复告诉他了。
我用几何证明了锐角下的和差公式,钝角无非就是直角加锐角,以此类推罢了。凡事最难的是从零到一,无数个0角也无法构成锐角。
参考资料
【反三角函数和差角公式】
【古诗文网:论语·述而篇】
【两脚和差公式】
【这些三角函数的名称是怎么来的?】
【数学大悲咒-三角函数之歌】
【三角函数之歌《trigonometric functions》】
【三角函数-和角化积-公式 动画演示推导过程】
【三角函数天才图解!一图牢记六大三角函数和差公式】
【对于arcsinx+arccosx=π/2(x∈[-1,1])的证明】
























 6001
6001

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










