预测数值型数据：回归（一）

　　机器学习算法的基本任务就是预测，预测目标按照数据类型可以分为两类：一种是标称型数据（通常表现为类标签），另一种是连续型数据（例如房价或者销售量等等）。针对标称型数据的预测就是我们常说的分类，针对数值型数据的预测就是回归了。这里有一个特殊的算法需要注意，逻辑回归（logistic regression）是一种用来分类的算法，那为什么又叫“回归”呢？这是因为逻辑回归是通过拟合曲线来进行分类的。也就是说，逻辑回归只不过在拟合曲线的过程中采用了回归的思想，其本质上仍然是分类算法。
　　假如我们要预测某一地区的房价，我们可能会列出以下的式子进行估计：
　　
　　　　　　　　　　　　　　　　　　　房价 = 0.7 * 面积 + 0.19 * 房子的朝向
　　
　　 这个简单的式子就叫回归方程，其中0.7和0.19称为回归系数，面积和房子的朝向称为特征。有了这些概念，我们就可以说，回归实际上就是求回归系数的过程。在这里我们看到，房价和面积以及房子的朝向这两个特征呈线性关系，这种情况我们称之为线性回归。当然还存在非线性回归，在这种情况下会考虑特征之间出现非线性操作的可能性（比如相乘或者相除），由于情况有点复杂，不在这篇文章的讨论范围之内。
　　简便起见，我们规定代表输入数据的矩阵为$\mathbf X$ （维度为m*n，m为样本数，n为特征维度），回归系数向量为 $\theta$（维度为n*1）。对于给定的数据矩阵$\mathbf X$ ，其预测结果由：$\mathbf Y= \mathbf X \theta$ 这个式子给出。我们手里有一些现成的x和y作为训练集，那么如何根据训练集找到合适的回归系数向量$\theta$是我们要考虑的首要问题，一旦找到$\theta$，预测问题就迎刃而解了。在实际应用中，我们通常认为能带来最小平方误差的$\theta$就是我们所要寻找的回归系数向量。平方误差指的是预测值与真实值的差的平方。采用平方这种形式的目的在于规避正负误差的互相抵消。所以，我们的目标函数如下所示：　　　

minθ∑i=0m(yi−xTiθ)2

$$min_\theta\sum_{i=0}^m (y_i-x_i^T\theta)^2$$
　　这里的m代表训练样本的总数。对这个函数的求解有很多方法，由于网络上对于详细解法的相关资料太少，下面展示一种利用正规方程组的解法：
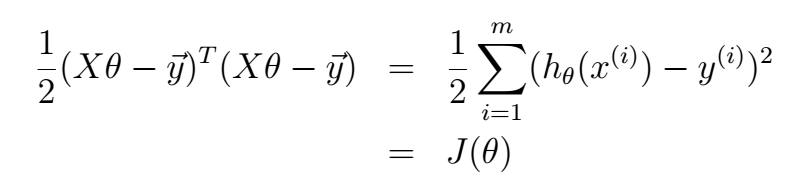(1)
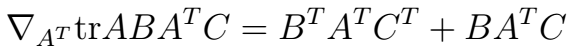　　　　　　$\nabla_AtrAB=B^T$(2)
　　针对上式不太清楚的朋友可以看我之前写的这篇博文：http://blog.csdn.net/qrlhl/article/details/47758509。根据以上式子，解法如下：

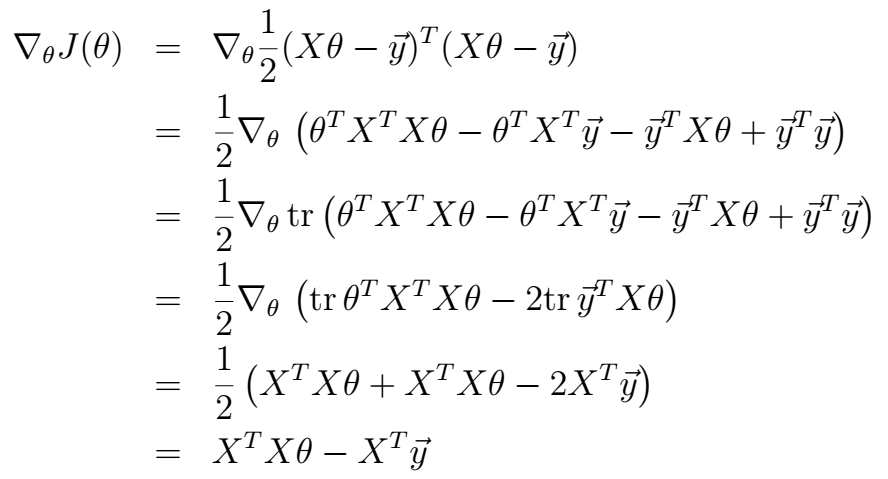
　　令其等于0，即可得：$\theta = (X^TX)^{-1}X^Ty$ 。有一些需要说明的地方：第三步是根据实数的迹和等于本身这一事实推导出的（括号中的每一项都为实数），第四步是根据式（2）推导出来的。第五步是根据式（1）推导出来的，其中的C为单位矩阵$I$。这样，我们就得到了根据训练集求得回归系数矩阵$\theta$的方程。这种方法的特点是简明易懂，不过缺点也很明显，就是$X^TX$ 这一项不一定可以顺利的求逆。由于只有满秩才可以求逆，这对数据矩阵$X$提出了一定的要求。有人也许会问$X^TX$不是满秩的情况下怎么办？这个时候就要用到岭回归（ridge regression）了，这一部分留到下次再讲。
　　说了这么久，放一张图上来看看线性回归的效果：

　　
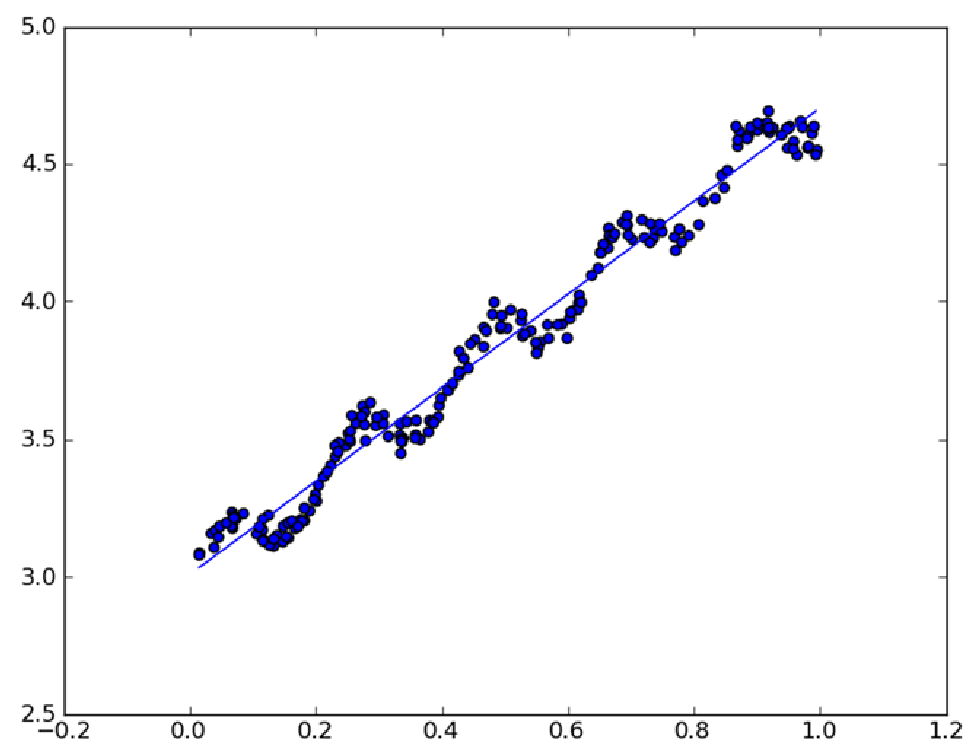
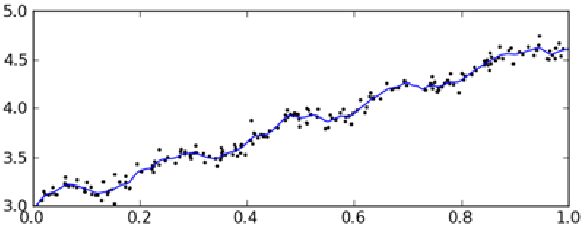
　　可以看到，直线较好的拟合了数据点的变化趋势，可以作出相对较好的预测。但是细心的朋友可能会发现，如果在数据点的每一段用一小段直线拟合也许会获得更加好的结果，就像这样：
　　
　　　　　　　　　　　　

　　这种方法叫做局部加权线性回归（Locally Weighted Linear Regression，LWLR），关于这种方法的细节，我们下次再说。