文章目录
前言
动笔写这个支持向量机(support vector machine)是比较纠结的,原因很简单,一者博主是刚开始接触机器学习,对一些问题的理解还是不够深刻,怕因为写错某句话而误导大家。二者这个东西本身就并不好懂,要深入学习和研究下去需花费不少时间和精力,三者这个东西也不好讲清楚,尽管网上已经有朋友写得不错了(见文末参考链接),望采纳。
我还是想尝试写一下,本文旨在讲述一下SVM的大体框架,具体详细的推导,以及涉及到的相关数学知识,博主推荐几篇博客,帮助读者去理解,鉴于博主本人能力有限,暂时还没法完全的手撕SVM。
本文在写的过程中,参考了不少资料,包括《机器学习实战》、《统计学习方法》《机器学习》及一些博客的支持向量机系列等等,于此,还是一篇学习笔记,只是加入了自己的理解和总结,有任何不妥之处,还望海涵。
一、简介
1.概述
支持向量机(SVM,也称为支持向量网络),支持向量机(support vector machines)是一种二分类模型,监督式学习 (Supervised Learning)的方法,主要用在统计分类 (Classification)问题和回归分析 (Regression)问题上。它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。是机器学习中获得关注最多的算法没有之一。
(1)由简至繁的模型包括:
当训练样本线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
当训练样本近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
当训练样本线性不可分时,通过核技巧和软间隔最大化,学习一个非线性支持向量机;
(2)从算法功能来看:

(3)从分类效力来讲:
SVM在无论线性还是非线性分类中,都是明星般的存在:
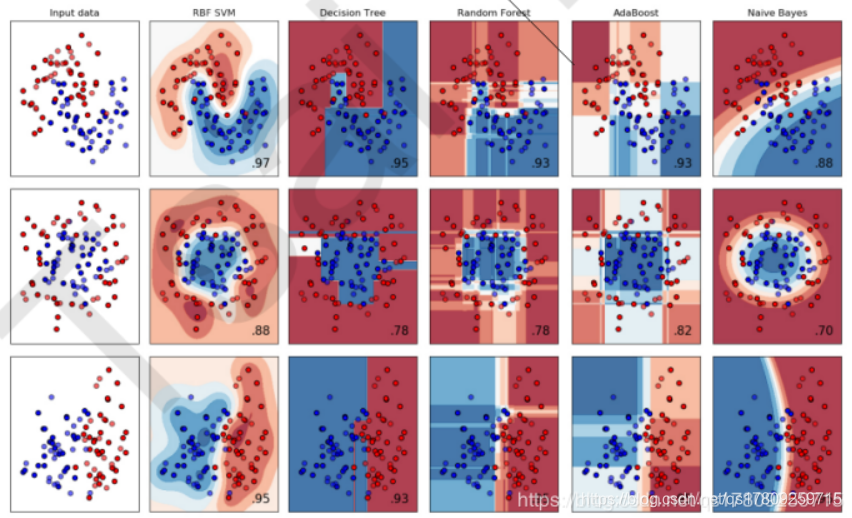
上图表示,根据输入数据集来看,对比SVM,Decision Tree, Random Forest, AdaBoost, Naive Bayes,每张图片右下角数字代表分类效果,从右下角的分类效果来看,SVM占有很大优势。
(4)从实际应用来看
SVM在各种实际问题中都表现非常优秀。它在手写识别数字和人脸识别中应用广泛,在文本和超 文本的分类中举足轻重,因为SVM可以大量减少标准归纳(standard inductive)和转换设置(transductive settings)中对标记训练实例的需求。同时,SVM也被用来执行图像的分类,并用于图像分割系统。实验结果表 明,在仅仅三到四轮相关反馈之后,SVM就能实现比传统的查询细化方案(query refifinement schemes)高出一大截的搜索精度。除此之外,生物学和许多其他科学都是SVM的青睐者,SVM现在已经广泛被用于蛋白质分类,现 在化合物分类的业界平均水平可以达到90%以上的准确率。在生物科学的尖端研究中,人们还使用支持向量机来识别用于模型预测的各种特征,以找出各种基因表现结果的影响因素。
(5)从学术的角度来看
SVM是最接近深度学习的机器学习算法。线性SVM可以看成是神经网络的单个神经元(虽然损失函数与神经网络不同),非线性的SVM则与两层的神经网络相当,非线性的SVM中如果添加多个核函数,则可以模仿多层的神经网络。而从数学的角度来看,SVM的数学原理是公认的对初学者来说难于上青天的水平,对于没有数学基础和数学逻辑熏陶的人来说,探究SVM的数学原理本身宛如在知识的荒原上跋涉。
当然了,没有算法是完美的,比SVM强大的算法在集成学习和深度学习中还有很多很多。
2.原理
支持向量机分类器,是在数据空间中找出一个超平面作为决策边界,利用这个决策边界来对数据进行分类,并使分类误差尽量小的模型,尤其在未知数据集上的分类误差(泛化误差)尽量小。
决策边界是比所在数据空间小一维的空间,在三维数据空间中就是一个平面,在二维数据空间中就是一条直线。
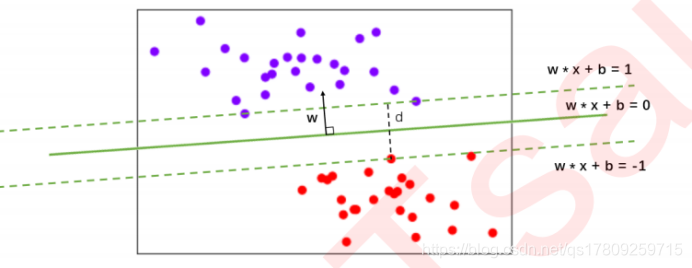
决策边界是比所在数据空间小一维的空间,在三维数据空间中就是一个平面,在二维数据空
间中就是一条直线。以二维数据为例,图中的数据集有两个特征,标签有两类,一类为紫色,一类为红色。对于这 组数据,我们找出的决策边界被表达为 ,决策边界把平面分成了上下两部分,决策边界以上的样本都分为一类,决策边界以下的样本被分为另一类。以我们的图像为例,绿色实现上部分为一类(全部都是紫色 点),下部分为另一类(全都是红色点)。
3.支持向量机原理的三层理解
目标是"找出边际最大的决策边界",听起来是一个十分熟悉的表达,这是一个最优化问题,而最优化问题往往和损失函数联系在一起。和逻辑回归中的过程一样,SVM也是通过最小化损失函数来求解一个用于后续模型使用的重要信息:决策边界。
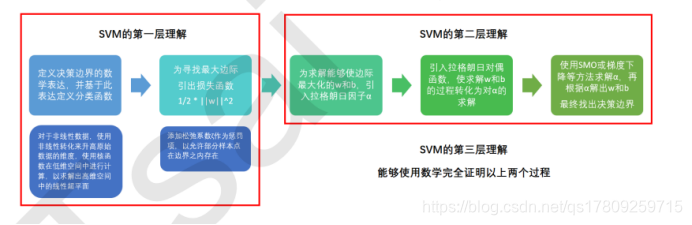
4.什么是支持向量(support vector)?

如图所示,支持向量 (Support Vector)是指在训练集 (Training data set)中,在分类时给予最多信息的点集合,被红色框围起来的这四个训练资料点就被称之为支持向量机。
支持向量就是与分类边界距离最近的训练资料点。从支持向量机的最佳化问题可以推导出一个重要性质:支持向量机的分类边界可由支持向量决定,而与其他资料点无关。这也是它们称为“支持向量”的原因。
5.什么是超平面(hyperplane)?
支持向量机建构一个或多个高维(甚至是无限多维)的超平面来分类资料点,这个超平面即为分类边界。直观来说,好的分类边界要距离最近的训练资料点越远越好,因为这样可以减低分类器的泛化误差。在支持向量机中,分类边界与最近的训练资料点之间的距离称为间隔(margin);支持向量机的目标即为找出间隔最大的超平面来作为分类边界。
参考博客: https://blog.csdn.net/xidiancoder/article/details/50913607?utm_source=app
二、线性可分支持向量机与硬间隔最大化
1.线性可分支持向量机


我们看一个简单的二维空间的例子,O代表正类,X代表负类,样本是线性可分的,但是很显然不只有这一条直线可以将样本分开,而是有无数条,我们所说的线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线。

直观看上去,能将训练样本分开的划分超平面有很多,但应该去找位于两类训练样本“正中间”的划分超平面,因为该划分超平面对训练样本局部扰动的“容忍”性最好,简言之,这个划分超平面所产生的结果是鲁棒性的。
间隔最大以及相应的约束最优化问题将在下面叙述,先介绍下函数间隔和几何间隔。
2.函数间隔和几何间隔
(1) 函数间隔(Functional Margin)
在超平面 ω T x + b = 0 ω^Tx+b=0 ωTx+b=0确定的情况下, ∣ ω T x + b ∣ |ω^Tx+b| ∣ωTx+b∣能够表示点x到超平面的距离远近,而通过观察 ω T x + b ω^Tx+b ωTx+b的符号与类型标记y符号是否一致,可以判断分类是否正确。
所以,我们可以用 y ∗ ( ω T x + b ) y*(ω^Tx+b) y∗(ωTx+b)的正负性来判定或表示分类的正确性。所以我们便在此处引出了函数间隔(Functional Margin)的概念。
定义函数间隔如下所示:

式(1.3.1)中参数含义如下:
- x x x:特征;
- y y y:结果标签;
- i i i:表示第i个样本;
而超平面 ( ω , b ) (ω,b) (ω,b)关于训练数据集T中所有样本点 ( x i , y i ) (xi,yi) (xi,yi)的函数间隔最小值,便成为超平面 ( ω , b ) (ω,b) (ω,b).关于T的函数间隔:

(2) 几何间隔(Geometrical Margin)
上面给出了函数间隔的定义,但这样定义的函数间隔有问题。比如成比例的改变 ω , b ω,b ω,b(如将他们都增大2倍),则函数间隔 f ( x ) f(x) f(x)的值变成了原来的2倍,但此时超平面却没有改变。所以只有函数间隔远远不够。
事实上,我们可以对法向量ω 加些约束条件,从而引出真正定义点到超平面的距离–几何间隔(geometrical margin)的概念。
所以在实际中,我们定义点到超平面的距离时,采用的是几何间隔。
假定对于一个点 x x x,令其垂直投影到超平面上的对应点为 x 0 x_0 x0,ω是垂直于超平面的一个向量,为样本 x x x到超平面的距离,如下图1.4所示:


3.间隔最大化
对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。

通过由前面的分析可知:函数间隔不适合用来最大化间隔值,因为在超平面固定以后,可以等比例地缩放w的长度和b的值,这样可以使得 f ( x ) = w T x + b f(x) = w^Tx + b f(x)=wTx+b的值任意大,亦即函数间隔 γ ^ \hat γ γ^可以在超平面保持不变的情况下被取得任意大。但几何间隔因为除上了 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣,使得在缩放w和b的时候几何间隔 γ ^ \hat γ γ^的值是不会改变的,它只随着超平面的变动而变动,因此,这是更加合适的一个间隔。换言之,这里要找的最大间隔分类超平面中的“间隔”指的是几何间隔。
于是最大间隔分类器(maximum margin classifier)的目标函数可以定义为:
m a x γ ^ max\hat γ maxγ^
同时需满足一些条件,根据间隔的定义,有

其中,s.t.,即subject to的意思,它导出的是约束条件。
回顾下几何间隔的定义

可知:如果令函数间隔 γ ^ \hat γ γ^等于1则有 γ ^ = 1 / ∣ ∣ w ∣ ∣ \hat γ= 1 / ||w|| γ^=1/∣∣w∣∣且 y i ( w T x i + b > = 1 , i , . . . . , n ) y_i(w^Tx_i+b>=1,i,....,n) yi(wTxi+b>=1,i,....,n)从而上述目标函数转化成了

相当于在相应的约束条件下

最大化这个 1 ∣ ∣ w ∣ ∣ \frac 1{||w||} ∣∣w∣∣1值,而 1 ∣ ∣ w ∣ ∣ \frac 1{||w||} ∣∣w∣∣1便是几何间隔 γ ^ \hat γ γ^。
如下图所示,中间的实线便是寻找到的最优超平面(Optimal Hyper Plane),其到两条虚线边界的距离相等,这个距离便是几何间隔 γ ^ \hat γ γ^,两条虚线间隔边界之间的距离等于 γ ^ \hat γ γ^,而虚线间隔边界上的点则是支持向量。由于这些支持向量刚好在虚线间隔边界上,所以它们满足 y ( w T x + b ) y(w^Tx+b) y(wTx+b)(还记得我们把 functional margin 定为 1 了吗?上节中:处于方便推导和优化的目的,我们可以令 γ ^ \hat γ γ^,而对于所有不是支持向量的点,则显然有 y ( w T x + b ) > 1 y(w^Tx+b)>1 y(wTx+b)>1。

4.学习的对偶算法
为了求解线性可分支持向量机的最优问题

将他作为最优化问题,应用拉格朗日对偶性,通过求解对偶问题(dual problem)得到原始问题(primal problem)的最优解,这就是线性可分支持向量机的对偶算法,这样做的优点,一是对偶问题往往更容易求解,二是引入核函数,进而推广到非线性分类问题。
首先构建拉格朗日函数(Lagrange function)。为此对每一个不等式约束引进拉格朗日橙子(Lagrange multiplier) α > = 0 , i = 1 , 2 , . . . . . , N α>=0,i = 1, 2, .....,N α>=0,i=1,2,.....,N,定义拉格朗日函数

根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题

先对 L ( w , b , a ) L(w,b,a) L(w,b,a)对 w , b w,b w,b的极小,也就是求偏导,令其等于0。然后在带进原式,求 α α α的 m a x max max,从而转化成求 α α α的min,得到与之等价的对偶问题的最优化问题:

详细推导过程参考:李航《统计学习方法》
三、线性支持向量机与软间隔最大化
1.线性支持向量机
上面所说的线性可分支持向量机是基于训练样本线性可分的理想状态,当训练样本中存在噪声或者特异点而造成线性不可分时,因为这时上述方法中的不等式约束并不能都成立,怎样才能将他扩展到线性不可分的问题呢?这就需要修改应间隔最大化,使其成为软间隔最大化,就需要用到下面讲到的线性支持向量机。

我们假设训练样本在样本空间或者特征空间中是线性可分的,但在现实任务中往往很难确定合适的核函数使训练集在特征空间中线性可分,退一步说,即使瞧好找到了这样的核函数使得样本在特征空间中线性可分,也很难判断是不是由于过拟合造成。
线性不可分意味着某些样本点$(xi,yi) $不能满足间隔大于等于1的条件,样本点落在超平面与边界之间。为解决这一问题,可以对每个样本点引入一个松弛变量 ξ i ≥ 0 ξi≥0 ξi≥0 ,使得间隔加上松弛变量大于等于1,这样约束条件变为:

同时,对于每一个松弛变量 ξ i ≥ 0 ξi≥0 ξi≥0,支付一个代价 ξ i ≥ 0 ξi≥0 ξi≥0,目标函数变为:

其中 C>0为惩罚参数,C值大时对误分类的惩罚增大, C值小时对误分类的惩罚减小,公式(21)包含两层含义:使 ∣ ∣ W 2 ∣ ∣ 2 \frac {||W_2||}{2} 2∣∣W2∣∣ 尽量小即间隔尽量大,同时使误分类点的个数尽量小,C是调和两者的系数。 有了公式(21),可以和线性可分支持向量机一样考虑线性支持向量机的学习过程,此时,线性支持向量机的学习问题变成如下凸二次规划问题的求解(原始问题):

2.学习的对偶算法
依旧构造拉格朗日函数,并转化为对偶问题:

3.支持向量
在软间隔最大化的情况下,
如下图,每个实例点到超平面的距离为
ζ
i
∣
∣
w
∣
∣
\frac {ζ_i} {||w||}
∣∣w∣∣ζi。
支持向量由间隔边界(如红圈点)、间隔边界与超平面之间(如绿圈点)或误分点(如蓝圈点)这些对分类起着关键作用的点组成。

4.合页损失函数


四、非线性支持向量机和核函数
1.非线性支持向量机
对于非线性问题,线性可分支持向量机并不能有效解决,要使用非线性模型才能很好地分类。先看一个例子,如下图,很显然使用直线并不能将两类样本分开,但是可以使用一条圆曲线(非线性模型)将它们分开。非线性问题往往不好求解,所以希望能用解线性分类问题的方法求解,因此可以采用非线性变换,将非线性问题变换成线性问题。

对于这样的问题,可以将训练样本从原始空间映射到一个更高维的空间,使得样本在这个空间中线性可分,如果原始空间维数是有限的,即属性是有限的,那么一定存在一个高维特征空间是样本可分。

令ϕ(x) 表示将 x 映射后的特征向量,于是在特征空间中,划分超平面所对应的的模型可表示为:

于是有最小化函数:

其对偶问题为:

若要对上式求解,会涉及到计算 Φ ( x i ) T Φ ( x j ) Φ(x_i)^TΦ(x_j) Φ(xi)TΦ(xj) 这是样本 Xi和Xj映射到特征空间之后的内积,由于特征空间的维数可能很高,甚至是无穷维,因此直接计算 Φ ( x i ) T Φ ( x j ) Φ(x_i)^TΦ(x_j) Φ(xi)TΦ(xj)通常是困难的,于是想到一个函数

即 x i x_i xi和 x j x_j xj在特征空间中的內积等于他们在原始样本空间汇总通过函数 K ( x i , x j ) K(x_i,x_j) K(xi,xj)计算的函数值,于是公式(16)写成如下:

求解后得到:

这里的函数 K ( x i , x j ) K(x_i,x_j) K(xi,xj)就是核函数。
2.常用核函数
通常人们会从一些常用的核函数中选择(根据问题和数据的不同,选择不同的参数,实际上就是得到了不同的核函数)。
(1)多项式核
多项式核形式如下:

(2)高斯核
高斯核形式如下:

这个核就是最开始提到过的,会将原始空间映射为无穷维空间的那个家伙。
不过,如果σ选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果σ选得很小,则可以将任意的数据映射为线性可分,当然这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。
不过总的来说,通过调控参数σ,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。下图2.4所示的例子便是把低维线性不可分的数据通过高斯核函数映射到了高维空间:

(3)线性核
线性核形式如下:

这个核实际上就是原始空间中的内积,它存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了。这里的意思是说,咱们写代码或写公式的时候,只要写个模板或通用表达式,然后再代入不同的核就可以了。这样便不用再分别写一个线性的,和一个非线性的,在形式上统一了起来。
(4)核函数的本质
上面说了这么多,还是要在这里概括一下核函数到底是什么东西。基本上就是三点:
- 实际中,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间中去,(映射到高维空间后,相关特征便被分开了,也就达到了分类的目的);
- 但进一步,如果凡是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到可怕的(即维度爆炸,如前文说的19维甚至无穷维的例子);
- 此时,核函数就隆重登场了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,也就如上文所说的避免了直接在高维空间中的复杂计算。
(5)举例说明一下核函数解决非线性问题的直观效果:
假设现在你是一个农场主,圈养了一批羊群,但为预防狼群袭击羊群,你需要搭建一个篱笆来把羊群围起来。但是篱笆应该建在哪里呢?你很可能需要依据牛群和狼群的位置建立一个分类器,比较下图这几种不同的分类器,我们可以看到SVM完成了一个很完美的解决方案。
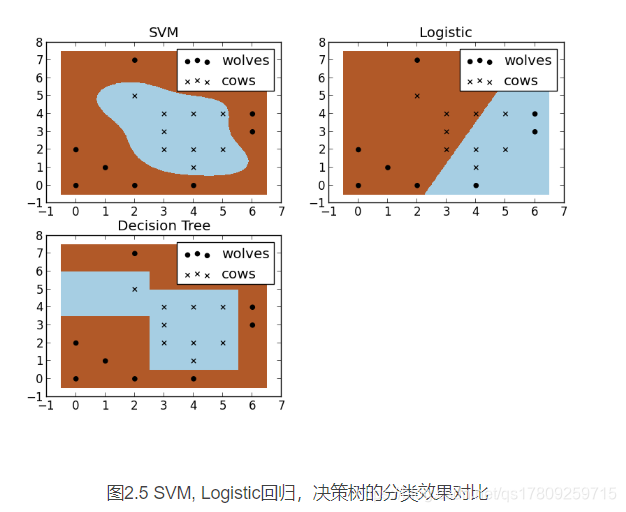
这个例子从侧面简单说明了SVM使用非线性分类器的优势,而逻辑模式以及决策树模式都是使用了直线方法。
五、序列最小优化算法SMO
1.SMO算法的基本思想

2.SMO算法总结

SMO 算法是支持向量机学习的一种快速算法,其特点是不断地将原二次规划问题分解为只有两个变量的二次规划子问题,并对子问题进行解析求解,直到所有变量满足KKT条件为止,这样通过启发式的方法得到原二次规划问题的最优解,因为子问题有解析解,所以每次计算子问题都很快,虽然计算子问题次数很多,但在总体上还是高效的.
详细的SMO算法参考:
博客:https://www.cnblogs.com/pinard/p/6111471.html
李航《统计学习方法》
六、线性SVM的详细推导
https://blog.csdn.net/c406495762/article/details/78072313
七、非线性的SVM的详细推导
https://blog.csdn.net/c406495762/article/details/78158354?utm_source=app
八、拉格朗日函数以及KKT条件
https://blog.csdn.net/xianlingmao/article/details/7919597
九、凸函数和凸优化理解
https://cloud.tencent.com/developer/news/335461
十、SVM的总结
1.不准确的说,SVM 它本质上即是一个分类方法。基本可以用如下内容来概括它的要点:
- 用 ω T + b ω^T+b ωT+b定义分类函数;
- 求 ω , b ω,b ω,b;
- 为了寻找最大间隔,引出 1 / 2 ∣ ∣ w ∣ ∣ 2 \frac {1/2}{||w||^2} ∣∣w∣∣21/2;
- 引入拉格朗日因子,化为对拉格朗日乘子 α α α的求解;
- 求解过程中,处理一系列最优化与凸二次规划的问题;
- 求解 α α α时可以使用快速学习方法SMO;
- 处理非线性情况时,使用核函数;
- 核函数在低维计算,等效了高维表现,避免了直接映射到高维计算时可能出现的维度爆炸现象;
2.支持向量机有如下优缺点。
优点:
- 对于线性不可分的情况可以通过核函数,映射到高维特征空间实现线性可分。
- SVM学习问题可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值。而其他分类方法(如基于规则的分类器和人工神经网络)都采用一种基于贪心学习的策略来搜索假设空间,这种方法一般只能获得局部最优解。
- 小集群分类效果好。
缺点:
- SVM仅仅只限于一个二类分类问题,对于多分类问题解决效果并不好。
- 仅局限于小集群样本,对于观测样本太多时,效率较低。
- 3.寻求合适的核函数相对困难。
参考:
[1]《统计学习方法》李航著
[2]《机器学习实战》Peter Harrington著
[3] https://www.cnblogs.com/pinard/p/6097604.html
[4] https://blog.csdn.net/b285795298/article/details/81977271
[5] https://blog.csdn.net/qq_35992440/article/details/80987664
[6] https://blog.csdn.net/sinat_20177327/article/details/79729551?utm_source=app
[7] https://blog.csdn.net/u014433413/article/details/78427574?utm_source=app
[8] https://blog.csdn.net/xidiancoder/article/details/50913607?utm_source=app
[9] https://blog.csdn.net/shijing_0214/article/details/50982602?utm_source=app
[10] https://blog.csdn.net/v_july_v/article/details/7624837
[11]https://blog.csdn.net/ajianyingxiaoqinghan/article/details/72897399





















 5214
5214











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








