本系列文章面向深度学习研发者,希望通过Image Caption Generation,一个有意思的具体任务,深入浅出地介绍深度学习的知识。本系列文章涉及到很多深度学习流行的模型,如CNN,RNN/LSTM,Attention等。本文为第5篇。
作者:李理
目前就职于环信,即时通讯云平台和全媒体智能客服平台,在环信从事智能客服和智能机器人相关工作,致力于用深度学习来提高智能机器人的性能。相关文章:
李理:从Image Caption Generation理解深度学习(part I)
李理:从Image Caption Generation理解深度学习(part II)
李理:从Image Caption Generation理解深度学习(part III)
李理:自动梯度求解 反向传播算法的另外一种视角
Optimization
这一部分内容来自:CS231n Convolutional Neural Networks for Visual Recognition
简介
我们的目标:x是一个向量,f(x)是一个函数,它的输入是一个向量(或者认为是多变量的函数,这个输入向量就是自变量),输出是一个实数值。我们需要计算的是f对每一个自变量的导数,然后把它们排成一个向量,也就是梯度。
为什么要求这个呢?前面我们也讲了,我们的神经网络的损失函数最终可以看成是权重weights和bias的函数,我们的目标就是调整这些参数,使得损失函数最小。
简单的表达式和梯度的解释
首先我们看一个很简单的函数 f(x,y)=xy,求f对x和y的偏导数很简单:
首先来看导数的定义:
函数在某个点的导数就是函数曲线在这个点的斜率,也就是f(x)随x的变化率。
比如上面的例子,当x=4,y=−3时 f(x,y)=−12,f对x的偏导数
也就是说,如果我们固定y=4,然后给x一个很小的变化h,那么f(x,y)的变化大约是-3*h。
因此乘法的梯度就是
同样,加法的梯度更简单:
最后一个简单函数是max函数:
这个导数是ReLU(x)=max(x,0)的导数,其实也简单,如果 x>=y,那么 max(x,y)=x,则导数是1,否则 max(x,y)=0,那么对x求导就是0。
复杂表达式的链式法则
接下来看一个稍微复杂一点的函数 f(x,y,z)=(x+y)z。我们引入一个中间变量q,f=qz,q=x+y,我们可以使用链式法则求f对x和y的导数。
对y的求导也是类似的。
下面是用python代码来求f对x和y的导数在某一个点的值。
# 设置自变量的值
x = -2; y = 5; z = -4
# “前向”计算f
q = x + y # q becomes 3
f = q * z # f becomes -12
# 从“后”往前“反向”计算
# 首先是 f = q * z
dfdz = q # 因为df/dz = q, 所以f对z的梯度是 3
dfdq = z # 因为df/dq = z, 所以f对q的梯度是 -4
# 然后 q = x + y
dfdx = 1.0 * dfdq # 因为dq/dx = 1,所以使用链式法则计算dfdx=-4
dfdy = 1.0 * dfdq # 因为dq/dy = 1,所以使用链式法则计算dfdy=-4
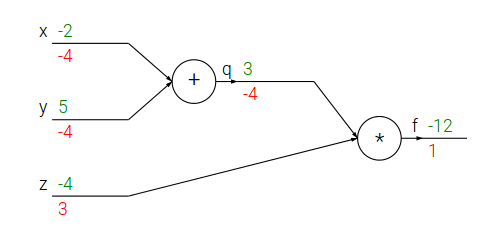
我们也可以用计算图来表示和计算:
绿色的值是feed forward的结果,而红色的值是backprop的结果。
不过我觉得cs231n课程的这个图没有上面blog的清晰,原因是虽然它标示出来了最终的梯度,但是没有标示出local gradient,我在下面会画出完整的计算过程。
反向传播算法的直觉解释
我们如果把计算图的每一个点看成一个“门”(或者一个模块),或者说一个函数。它有一个输入(向量),也有一个输出(标量)。对于一个门来说有两个计算,首先是根据输入,计算输出,这个一般很容易。还有一种计算就是求输出对每一个输入的偏导数,或者说输出对输入向量的”局部“梯度(local gradient)。一个复杂计算图(神经网络)的计算首先就是前向计算,然后反向计算,反向计算公式可能看起来很复杂,但是如果在计算图上其实就是简单的用local gradient乘以从后面传过来的gradient,然后加起来。
Sigmoid模块的例子
接下来我们看一个更复杂的例子:
这个函数是一个比较复杂的复合函数,但是构成它的基本函数是如下4个简单函数:
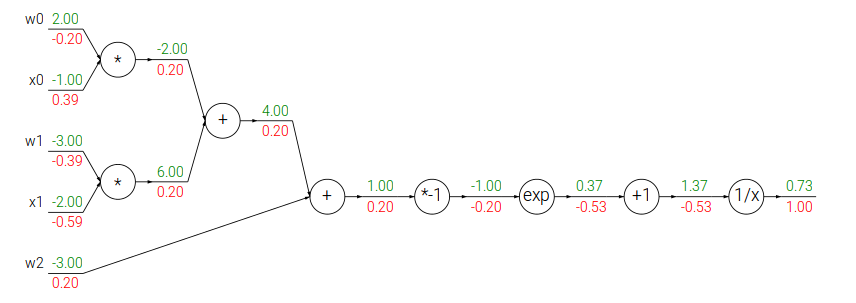
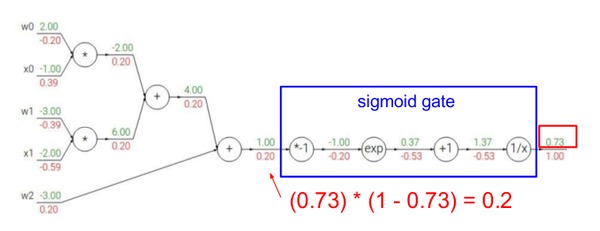
下面是用计算图画出这个计算过程:
这个图有4种gate,加法,乘法,指数和倒数。加法有加一个常数和两个变量相加,乘法也是一样。
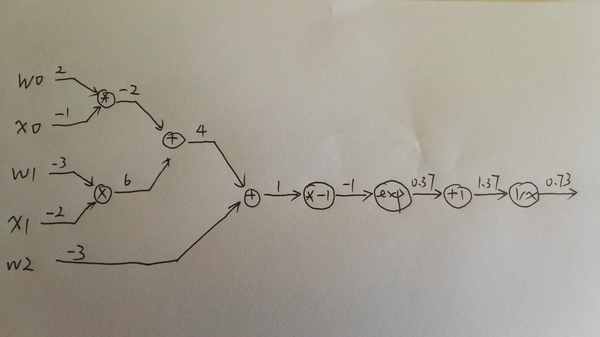
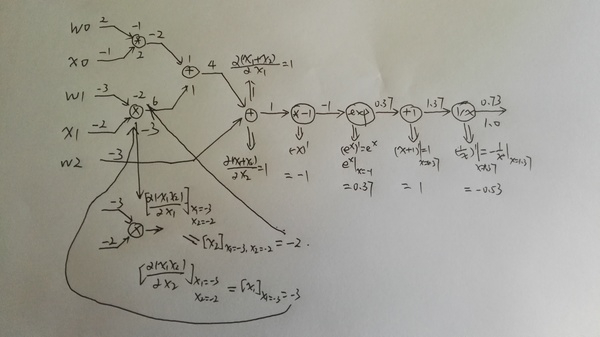
上图绿色的值是前向计算的结果,而红色的值是反向计算的结果,local graident并没有标示出来,所以看起来可能有些跳跃,下面我在纸上详细的分解了其中的步骤,请读者跟着下图自己动手计算一遍。
上图就是前向计算的过程,比较简单。
第二个图是计算local gradient,对于两个输入的乘法和加法,local gradient也是两个值,local gradient的值我是放到图的节点上了。
第三个图是具体计算一个乘法的local gradient的过程,因为上图可能看不清,所以单独放大了这一步。
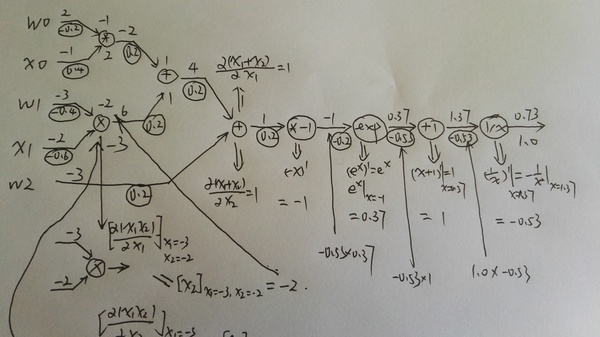
最后计算真正的梯度,是把local gradient乘以来自上一步的gradient。不过这个例子一个节点只有一个输出,如果有多个的话,梯度是加起来的,可以参考1.4的
上面我们看到把
分解成最基本的加法,乘法,导数和指数函数,但是我们也可以不分解这么细。之前我们也学习过了sigmoid函数,那么我们可以这样分解:
σ(x)σ(x) 的导数我们之前已经推导过一次了,这里再列一下:
因此我们可以把后面一长串的gate”压缩“成一个gate:
我们来比较一下,之前前向计算 σ(x)σ(x) 需要一次乘法,一次exp,一次加法导数;而反向计算需要分别计算这4个gate的导数。
而压缩后前向计算是一样的,但是反向计算可以”利用“前向计算的结果
这只需要一次减法和一次乘法!当然如果不能利用前向的结果,我们如果需要重新计算 σ(x)σ(x) ,那么压缩其实没有什么用处。能压缩的原因在于σ函数导数的特殊形式。而神经网络的关键问题是在训练,训练性能就取决于这些细节。如果是我们自己来实现反向传播算法,我们就需要利用这样的特性。而如果是使用工具,那么就依赖于工具的优化水平了。
下面我们用代码来实现一下:
w = [2,-3,-3] # assume some random weights and data
x = [-1, -2]
# forward pass
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid function
# backward pass through the neuron (backpropagation)
ddot = (1 - f) * f # gradient on dot variable, using the sigmoid gradient derivation
dx = [w[0] * ddot, w[1] * ddot] # backprop into x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # backprop into w
# we're done! we have the gradients on the inputs to the circuit
上面的例子用了一个小技巧,就是所谓的staged backpropagation,说白了就是给中间的计算节点起一个名字。比如dot。为了让大家熟悉这种技巧,下面有一个例子。
Staged computation练习
我们用代码来计算这个函数对x和y的梯度在某一点的值
前向计算
x = 3 # example values
y = -4
# forward pass
sigy = 1.0 / (1 + math.exp(-y)) # 分子上的sigmoid #(1)
num = x + sigy # 分子 #(2)
sigx = 1.0 / (1 + math.exp(-x)) # 分母上的sigmoid #(3)
xpy = x + y #(4)
xpysqr = xpy**2 #(5)
den = sigx + xpysqr # 分母 #(6)
invden = 1.0 / den #(7)
f = num * invden # done! #(8)反向计算
# backprop f = num * invden
dnum = invden # gradient on numerator #(8)
dinvden = num #(8)
# backprop invden = 1.0 / den
dden = (-1.0 / (den**2)) * dinvden #(7)
# backprop den = sigx + xpysqr
dsigx = (1) * dden #(6)
dxpysqr = (1) * dden #(6)
# backprop xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr #(5)
# backprop xpy = x + y
dx = (1) * dxpy #(4)
dy = (1) * dxpy #(4)
# backprop sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # Notice += !! See notes below #(3)
# backprop num = x + sigy
dx += (1) * dnum #(2)
dsigy = (1) * dnum #(2)
# backprop sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy #(1)
# done! phew需要注意的两点:1. 前向的结果都要保存下来,反向的时候要用的。2. 如果某个变量有多个出去的边,第一次是等于,第二次就是+=,因为我们要把不同出去点的梯度加起来。
下面我们来逐行分析反向计算:
(8) f = num * invden
local gradient
而上面传过来的梯度是1,所以 dnum=1∗invden。注意变量的命名规则, df/dnum就命名为dnum【省略了df,因为默认我们是求f对所有变量的偏导数】
同理: dinvden=num
(7) invden = 1.0 / den
local gradient是 (−1.0/(den∗∗2)) ,然后乘以上面来的dinvden
(6) den = sigx + xpysqr
这个函数有两个变量sigx和xpysqr,所以需要计算两个local梯度,然后乘以dden
加法的local梯度是1,所以就是(1)*dden
(5) xpysqr = xpy**2
local gradient是2*xpy,再乘以dxpysqr
(4) xpy = x + y
还是一个加法,local gradient是1,所以dx和dy都是dxpy乘1
(3) sigx = 1.0 / (1 + math.exp(-x))
这是sigmoid函数,local gradient是 (1-sigx)*sigx,再乘以dsigx。
不过需要注意的是这是dx的第二次出现,所以是+=,表示来自不同路径反向传播过来给x的梯度值
(2) num = x + sigy
还是个很简单的加法,local gradient是1。需要注意的是dx是+=,理由同上。
(1) sigy = 1.0 / (1 + math.exp(-y))
最后是sigmoid(y)和前面(3)一样的。
请仔细阅读上面反向计算的每一步代码,确保自己理解了之后再往下阅读。
梯度的矩阵运算
前面都是对一个标量的计算,在实际实现时用矩阵运算一次计算一层的所有梯度会更加高效。因为矩阵乘以向量和向量乘以向量都可以看出矩阵乘以矩阵的特殊形式,所以下面我们介绍矩阵乘法怎么求梯度。
首先我们得定义什么叫矩阵对矩阵的梯度!
我查阅了很多资料,也没找到哪里有矩阵对矩阵的梯度的定义,如果哪位读者知道,请告诉我,谢谢!唯一比较接近的是Andrew Ng的课程cs294的背景知识介绍的slides linalg的4.1节定义了gradient of Matrix,关于矩阵对矩阵的梯度我会有一个猜测性的解释,可能会有问题。
首先介绍graident of matrix
假设 f:Rm×n→R是一个函数,输入是一个m×n的实数值矩阵,输出是一个实数。那么f对A的梯度是如下定义的:
看起来定义很复杂?其实很简单,我们把f看成一个mn个自变量的函数,因此我们可以求f对这mn个自变量的偏导数,然后把它们排列成m*n的矩阵就行了。为什么要多此一举把变量拍成矩阵把他们的偏导数也排成矩阵?想想我们之前的神经网络的weights矩阵,这是很自然的定义,同时我们需要计算loss对weights矩阵的每一个变量的偏导数,写出这样的形式计算起来比较方便。
那么什么是矩阵对矩阵的梯度呢?我们先看实际神经网络的一个计算情况。对于全连接的神经网络,我们有一个矩阵乘以向量 D=WxD=Wx 【我们这里把向量x看成矩阵】。现在我们需要计算loss对某一个 WijWij 的偏导数,根据我们之前的计算图, WijWij 有多少条出边,那么就有多少个要累加的梯度乘以local梯度。
假设W是m×n的矩阵,x是n×p的矩阵,则D是m×p的矩阵
根据矩阵乘法的定义
我们可以计算:
请仔细理解上面这一步,如果 k≠i,则不论s是什么,Wks跟Wij不是同一个变量,所以导数就是0;如果k=i,∑sWisxsl=xjl,也就求和的下标s取j的时候有WijWij。
因此
上面计算了loss对一个Wij的偏导数,如果把它写成矩阵形式就是:
前面我们推导出了对Wij的偏导数的计算公式,下面我们把它写成矩阵乘法的形式并验证【证明】它。
为什么可以写成这样的形式呢?
上面的推导似乎很复杂,但是我们只要能记住就行,记法也很简单——把矩阵都变成最特殊的1 1的矩阵(也就是标量,一个实数)。D=w x,这个导数很容易吧,对w求导就是local gradient x,然后乘以得到dW=dD x;同理dx=dD W。
但是等等,刚才那个公式里还有矩阵的转置,这个怎么记?这里有一个小技巧,就是矩阵乘法的条件,两个矩阵能相乘他们的大小必须匹配,比如D=Wx,W是m n,x是n p,也就是第二个矩阵的行数等于第一个的列数。
现在我们已经知道dW是dD”乘以“x了,dW的大小和W一样是m n,而dD和D一样是m p,而x是n p,那么为了得到一个m n的矩阵,唯一的办法就是 dD∗xT
同理dx是n p,dD是m p,W是m*n,唯一的乘法就是 WT∗dD
下面是用python代码来演示,numpy的dot就是矩阵乘法,可以用numpy.dot(A,B),也可以直接调用ndarray的dot函数——A.dot(B):
# forward pass
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)
# now suppose we had the gradient on D from above in the circuit
dD = np.random.randn(*D.shape) # same shape as D
dW = dD.dot(X.T) #.T gives the transpose of the matrix
dX = W.T.dot(dD)至此,本系列文章的第5部分告一段落。在接下来的文章中,作者将为大家详细讲述关于常见的深度学习框架/工具的使用方法、使用自动求导来实现多层神经网络等内容,敬请期待。
本系列文章也将在CSDN人工智能公众号AI_Thinker中进行连载,扫描下方二维码即可关注。







 本文介绍了自动梯度求解在深度学习中的重要性,通过cs231n课程的内容,详细讲解了反向传播算法的直观解释,包括链式法则的应用、Sigmoid函数的导数计算以及矩阵运算中的梯度计算。通过实例展示了如何利用计算图进行前向和反向计算,并探讨了优化中的梯度计算技巧。
本文介绍了自动梯度求解在深度学习中的重要性,通过cs231n课程的内容,详细讲解了反向传播算法的直观解释,包括链式法则的应用、Sigmoid函数的导数计算以及矩阵运算中的梯度计算。通过实例展示了如何利用计算图进行前向和反向计算,并探讨了优化中的梯度计算技巧。
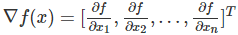

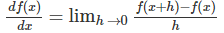
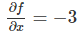
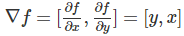
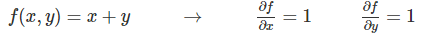
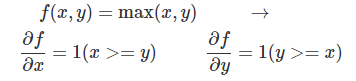
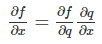
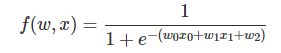
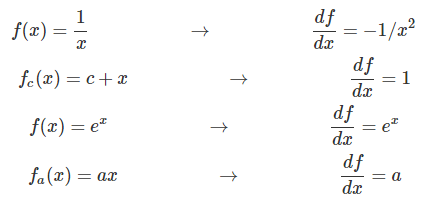
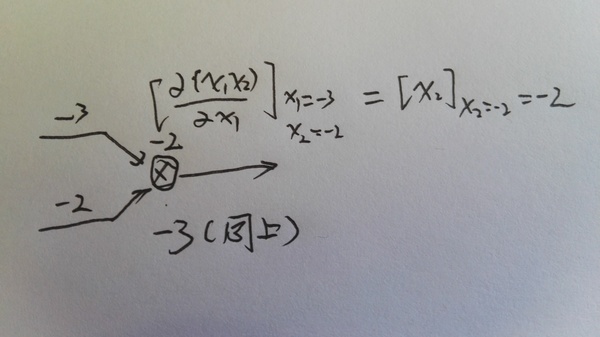
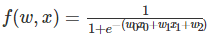
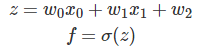
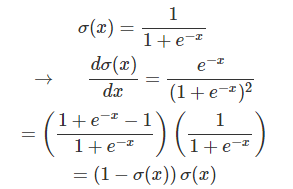
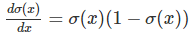
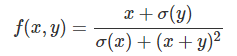
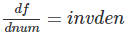

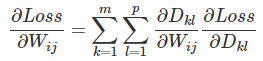
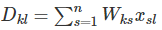
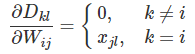

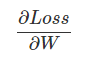
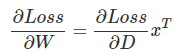
















 1420
1420

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








