beta分布介绍
如下为beta分布的形式,其分布有两个参数,
α
和
β
。其分布形式如下
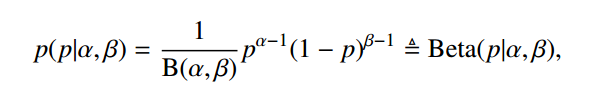
其中,
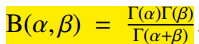
Γ(x)
是Gamma函数。其中beta分布定义域为【0,1】
可以看出
Bernoulli实验
伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验。其特点是该随机试验只有两种可能结果:发生或者不发生。如下,发生的概率为
p
,不发生的概率为
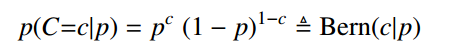
比如掷硬币,这里定义 c=1 表示正面向上,否则 c=0 表示反面向上。
共轭
在做贝叶斯估计时,有
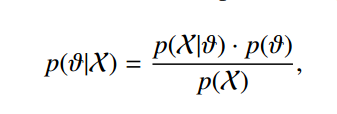
即后验分布 = 似然函数* 先验分布/ P(X)。
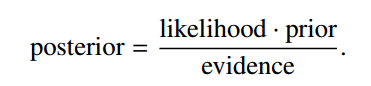
之所以采用共轭先验的原因是可以使得先验分布和后验分布的形式相同,这样计算起来就较为方便。为了使得先验分布和后验分布的形式相同,我们定义:如果先验分布和似然函数可以使得先验分布和后验分布有相同的形式,那么就称某参数的共轭先验分布。
一般性的定义如下:设
θ
为总体分布中的参数(或参数向量),
π(θ)
为先验的概率密度函数,加入由抽取的信息计算得到的后验概率密度函数与
π(θ)
具有相同的函数形式,则称
π(θ)
为
θ
的共轭先验分布。
需要指出,共轭先验分布是对某一分布的参数而言的,如正太分布的均值、正太分布的方差,离开指定参数以及所在的分布去谈共轭先验分布式没有任何意义的。
如下,还以掷硬币为例,我们依据已有的样本来推测正面向上的概率 p 。基于贝叶斯公式可知其后验概率如下:
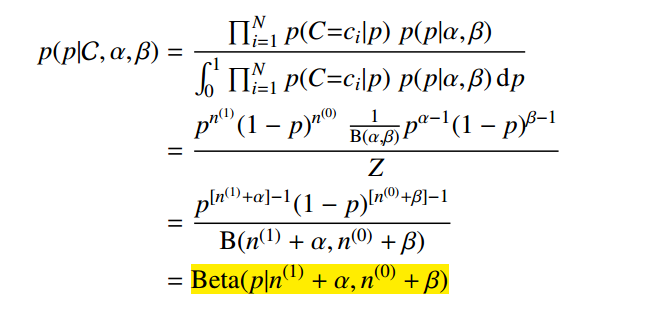
可以看出推测的后验概率公式与先验形式一致。
同时,我们还能计算得到分母
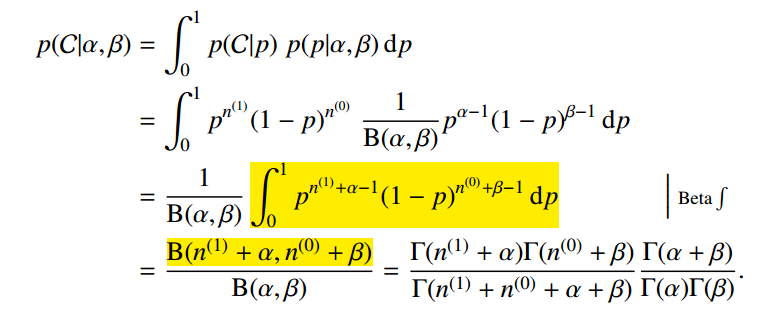
利用上面两个式子便可以预测下一次正面向上的概率。
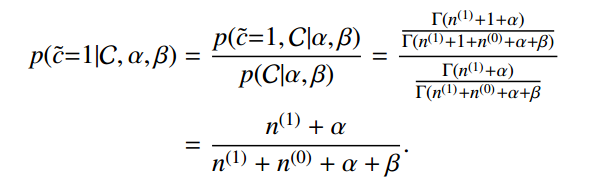
期望与方差
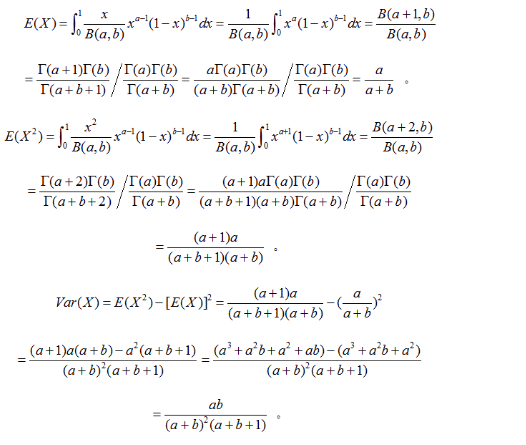
在beta-Bernoulli process中也有应用
参考论文:Heinrich G. Parameter estimation for text analysis[J]. University of Leipzig, Tech. Rep, 2008.
An introduction to Bayesian nonparametrics Lecture 2: The Indian buffet process










 本文介绍了Beta分布及其在贝叶斯估计中的应用。详细解释了Beta分布的形式及参数,探讨了它与Bernoulli实验的关系,并展示了如何通过共轭先验简化计算过程。
本文介绍了Beta分布及其在贝叶斯估计中的应用。详细解释了Beta分布的形式及参数,探讨了它与Bernoulli实验的关系,并展示了如何通过共轭先验简化计算过程。

















 1552
1552

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








