FIR滤波器以及吉布斯效应

最近要录一些环境声音数据做实验，录音笔上有一个选项——Low Cut Filter，即低频切除滤波器，就是一个高通滤波器，其作用是“减轻投影机声音或因风产生的啸叫声等低频噪音，以便更清晰地录制文件“，截止频率可调。
于是，考虑自己设计一个滤波器以实现这一功能，打算使用FIR滤波器。

---

滤波器设计指标

关于滤波器的设计指标，xiahouzuoxin的这篇文章介绍得很详细。不过里面有一小点讲错：衰减指标的分贝值应定义为$10log\frac{P_{out}}{P_{in}}$或者$20log\frac{V_{out}}{V_{in}}$，注意其中使用功率比和幅值比时常系数的差别。

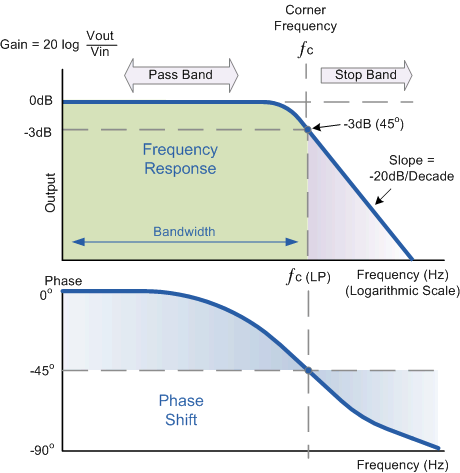
图1 低通滤波器

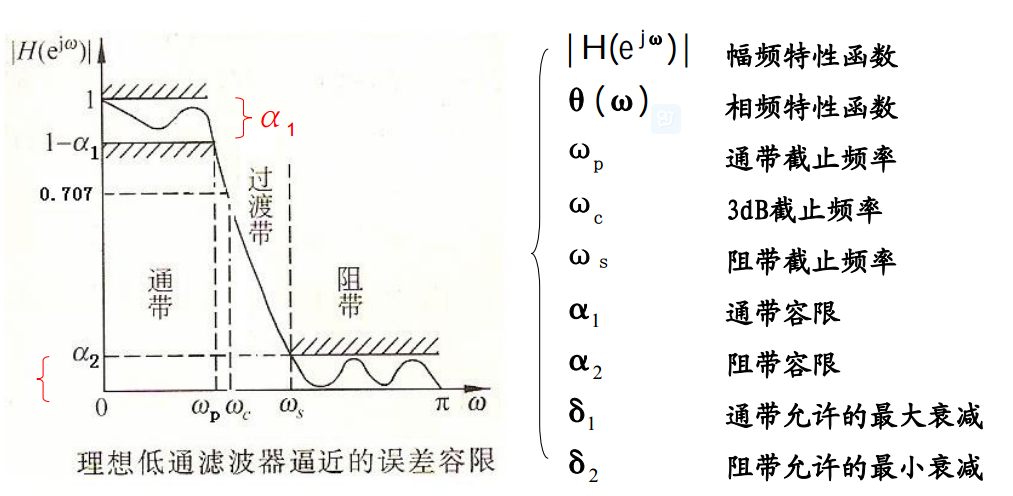
图2 滤波器设计指标（对应低通滤波器）

关于图1和图2的说明：

• 图1的幅频特性单位为dB，是按通带增益为1归一化后的结果。图1中的3dB衰减即对应图2中的0.707（由$20log\frac{V_{-3dB}}{V_{0dB}}=-3$得$V_{-3dB}=0.707$），即在此点处信号幅值衰减至原来的0.707，而功率衰减至原来的一半。工程上，通常以3dB截止频率来计算带宽。
• 几个特征频率
  
  • 通带截止频率$\omega_p$：通带与过渡带边界点的频率
  • 阻带截止频率$\omega_s$：阻带与过渡带边界点的频率
  • 3dB截止频率$\omega_c$：信号功率衰减至一半的频率
• 增益与衰减
  
  • 通带增益：对于低通为$\omega=0$时的增益，对于高通为$\omega\rightarrow\infty$时的增益，对于带通为中心频率处的增益
  • 通带容限$\alpha_1$：通带内，$1-\alpha_1\le |H(e^{j\omega})|\le1+\alpha_1,|\omega|\le\omega_p$
  • 通带衰减$\delta_1$：相对于通带增益，通带内波纹允许的最大衰减，其分贝值为$\delta_1=20log\frac{H(e^{j0})}{H(e^{j\omega_p})}=-20log(1-\alpha_1)$
  • 阻带容限$\alpha_2$：阻带内，$|H(e^{j\omega})|\le\alpha_2,\omega_s\le\omega\le\pi$
  • 阻带衰减$\delta_2$：相对于通带增益，阻带内波纹允许的最小衰减，其分贝值为$\delta_2=20log\frac{H(e^{j0})}{H(e^{j\omega_s})}=-20log(\alpha_2)$
• 物理频率与角频率的关系：$\omega=2\pi f$。同时，对于采样频率为$f_s$的信号，根据Nyquist采样定律，信号的最高频率为$\frac{f_s}{2}$，所以频谱反映的是0~$\frac{f_s}{2}$的谱信息，对应角频率0~$\pi$（离散时间实信号的频谱共轭对称且以$2\pi$为周期）。

---

FIR滤波器的设计

FIR滤波器，即有限长单位脉冲响应滤波器，具有两个突出的特点：线性相位和稳定性。

• 稳定性：FIR滤波器的单位脉冲响应为有限长，其$z$变换收敛
• 线性相位：如果FIR滤波器的单位脉冲响应是实数，且满足偶对称或奇对称的条件，则滤波器就具有严格的线性相位特性。
  
  • 偶对称：$h[n]=h[N-1-n]\rightarrow \\ H(e^{j\omega})=e^{-j\omega(\frac{N-1}{2})}\sum_{n=0}^{N-1}h[n]\cos[\omega(n-\frac{N-1}{2})]\\\phi(\omega)=e^{-\omega\frac{N-1}{2}}$
  • 奇对称：$h[n]=-h[N-1-n]\rightarrow \\ H(e^{j\omega})=e^{-j[\omega(\frac{N-1}{2})+\frac{\pi}{2}]}\sum_{n=0}^{N-1}h[n]\sin\{\omega(n-\frac{N-1}{2})\}\\\phi(\omega)=e^{-\omega\frac{N-1}{2}-\frac{\pi}{2}}$

  理解线性相位

  线性相位特性是指系统的相频特性是一条直线，其意义在于系统对所有频率的信号均产生相同的时延，不会发生相位失真。

  线性系统引起的信号失真由两方面因素造成——
  1. 幅度失真：系统对信号中各频率分量的幅度产生不同程度的衰减
  2. 相位失真：系统对信号中各频率分量产生的相移不与频率成正比，使响应的各频率分量在时间轴上产生不同的时延，其相对位置产生变化（频域相移对应于时域时移）

  设滤波器频响为
  

  $$H(\omega)=A(\omega)e^{j\phi(\omega)}$$ 对于线性相位滤波器，有 $\phi(\omega)=\alpha\omega+\beta$， $\alpha、\beta$为常数。
  考虑频率为 $\omega_0$的复正弦信号，
  $$x(t)=e^{j\omega_0t}\rightarrow X(\omega)=2\pi\delta(\omega-\omega_0)$$ 通过系统 $H(\omega)$后，有 $$Y(\omega)=X(\omega)H(\omega)=2\pi\delta(\omega-\omega_0)A(\omega)e^{j\phi(\omega)}=2\pi\delta(\omega-\omega_0)A(\omega_0)e^{j\phi(\omega_0)}$$ $$\rightarrow y(t)=A(\omega_0)e^{j\omega_0(t+\frac{\phi(\omega_0)}{\omega_0})}$$ 对于线性相位系统，有
  $$y_{lp}(t)=A(\omega_0)e^{j(\omega_0(t+\alpha)+\beta)}$$ 即 信号$x(t)$通过系统后产生$\alpha$的时延，而且当$\beta\ne 0$时，将产生相移$\beta$。而对于非线性相位系统，这个时延与 $\omega_0$有关。进一步，任意信号均可分解成一系列复正弦信号的加权和。对于线性相位系统，不同频率的复正弦信号通过系统后均产生相同的时延，而非线性相位系统可能会对信号造成失真或变形。

  四种线性相位FIR滤波器

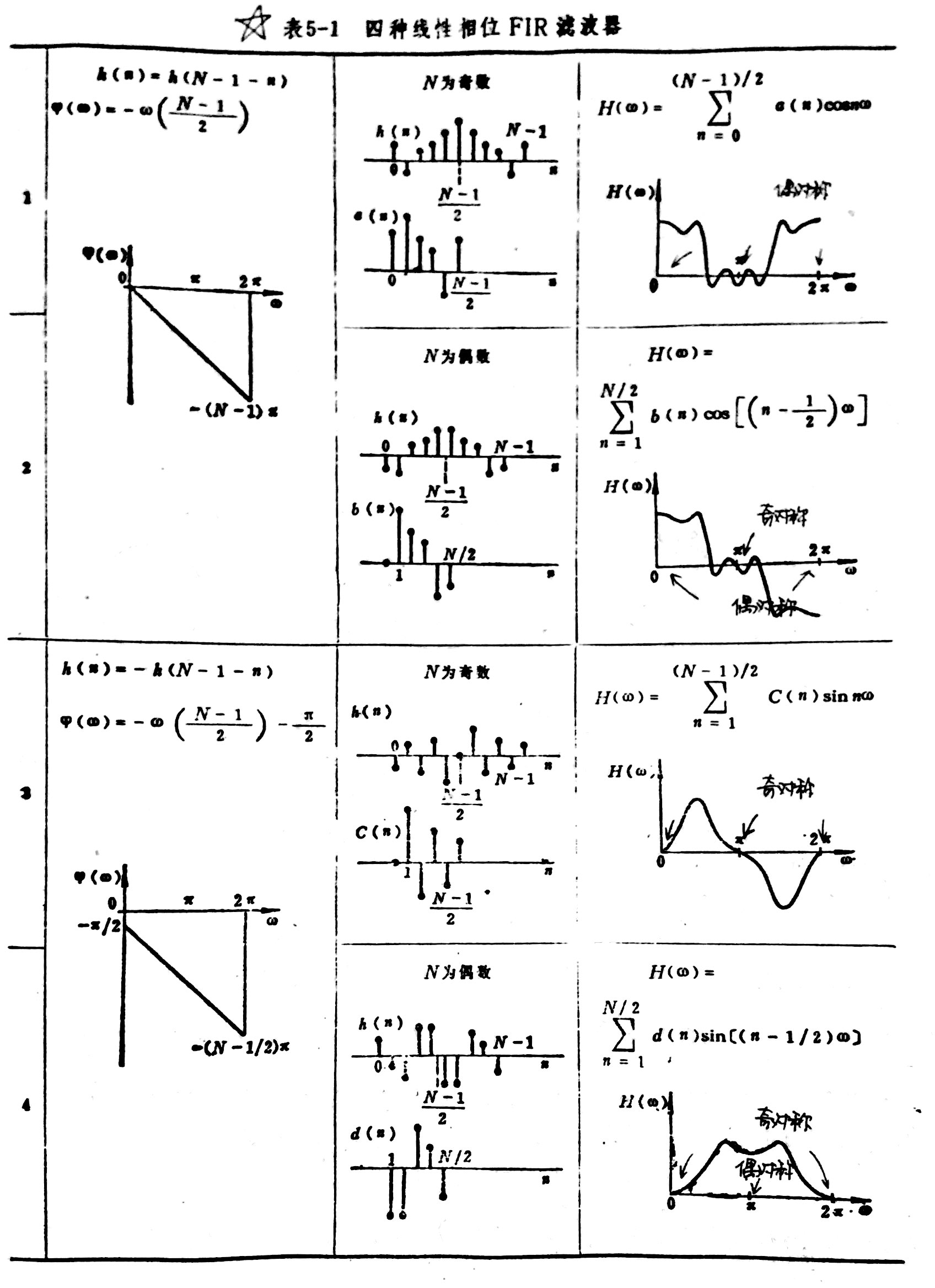
  根据$N$的奇偶、$h[n]$奇对称还是偶对称的情况，可分别对应四种滤波器。为设计出线性相位的FIR滤波器，需根据滤波器的设计要求（低通、高通、带通、带阻）确定对应的$h[n]$应满足的条件。

  表1 四种线性相位FIR滤波器[3]
  

  上表中最右列为滤波器的幅频特性$H(\omega)$，即$H(e^{j\omega})=H(\omega)e^{j\phi(\omega)}$。这里要注意虽然$H_(e^{j\omega})$是以$2\pi$为周期的，但不等价于$H(\omega)$也是以$2\pi$为周期。以$\phi(\omega)=-\alpha\omega-\beta$为例，
  

  $$H(e^{j(\omega+2\pi)})=H(\omega+2\pi)e^{-j(\alpha(\omega+2\pi)+\beta)}=H(\omega+2\pi)e^{-j(\alpha\omega+\beta)}e^{-j2\pi\alpha}$$ 因此有
  $$H(\omega+2\pi)e^{-j2\pi\alpha}=H(\omega)$$ 当 $\alpha\in \Bbb{Z}$时， $H(\omega+2\pi)=H(\omega)$，对应表中第1、3种情况；
  当 $\alpha=m+\frac12,m\in \Bbb{Z}$时， $H(\omega+2\pi)=-H(\omega)$，对应表中第2、4种情况。

  ---

  窗口法设计FIR滤波器

  窗口法设计FIR滤波器的基本思路是依据希望得到的理想滤波器的频响$H_d(e^{j\omega})$，计算其单位脉冲响应$h_d[n]$，从中直接截取一段$h[n]$以逼近理想值。同时，为保证线性相位特性，$h[n]$需满足对应的偶对称或奇对称特性。
  例1：截止频率为$\omega_c$的理想低通滤波器
  根据表1，所设计的滤波器为I、II类。设时延为$\alpha$，理想滤波器频响为
  

  $$H_d(e^{j\omega})=\{_{0,\quad\ \ \omega_c\lt|\omega|\lt\pi}^{e^{-j\omega\alpha},\ |\omega|\le\omega_c}$$ 计算其单位脉冲响应，为 $$h_d[n]=\frac1{2\pi}\int_{-\omega_c}^{\omega_c}e^{-j\omega\alpha}e^{j\omega n}d\omega=\frac{e^{j\omega(n-\alpha)}}{2\pi j(n-\alpha)}|_{-\omega_c}^{\omega_c}=\frac{\sin[\omega_c(n-\alpha)]}{\pi(n-\alpha)}$$ 这是一个以 $\alpha$为中心的偶对称的无限长非因果序列。所截取的 $h[n]$需满足偶对称， $N$可奇可偶，因此 $$h[n]=\{_{0,\quad \ \ \ else}^{h_d[n],\ 0\le n\le N-1}$$ $$\alpha=\frac{N-1}{2}$$

  例2：截止频率为$\omega_c$的理想高通滤波器
  根据表1，所设计的滤波器为IV类。设时延为$\alpha$，理想滤波器频响为
  

  $$H_d(e^{j\omega})=\{_{0,\quad\ \ \ \ \ 0\le\omega\lt\omega_c\ and\ 2\pi-\omega_c\lt\omega\le2\pi}^{e^{-j(\omega\alpha+\frac{\pi}{2})},\ \omega_c\le\omega\le2\pi-\omega_c}$$ 其单位脉冲响应为 $$h_d[n]=\frac1{2\pi}\int_{\omega_c}^{2\pi-\omega_c}e^{-j(\omega\alpha+\frac{\pi}{2})}e^{j\omega n}d\omega=\frac{e^{-j\frac{\pi}{2}}e^{j\omega(n-\alpha)}}{2\pi j(n-\alpha)}|_{\omega_c}^{2\pi-\omega_c}=\frac{e^{j\omega_c(n-\alpha)}-e^{j2\pi(n-\alpha)}e^{-j\omega_c(n-\alpha)}}{2\pi (n-\alpha)}\xrightarrow{\alpha=m+\frac12,m\in\Bbb Z}=\frac{\cos[\omega_c(n-\alpha)]}{\pi(n-\alpha)}$$
  这是一个以 $\alpha$为中心的奇对称的无限长非因果序列。截取的 $h[n]$需满足奇对称，且 $N$为偶数，因此 $$h[n]=\{_{0,\quad \ \ \ else}^{h_d[n],\ 0\le n\le N-1}$$ $$\alpha=\frac{N-1}{2}$$ 在这里， $h[n]$可看做是 $h_d[n]$与一个窗口函数的乘积，上例中使用的是矩形窗函数 $R_N[n]$。对于一般的 $N$点窗函数$w[n]$，有 $$h[n]=h_d[n]w[n]$$ 这样，只要给定截止频率，选择一个窗函数和点数，我要设计的LCF就可以搞定啦。

  ---

  窗函数的影响

  这种对理想单位脉冲响应加窗的处理对频响将产生什么影响？以及逼近质量如何？
  

  $$h[n]=h_d[n]w[n]\rightarrow H(e^{j\omega})=\frac1{2\pi}H_d(e^{j\omega})* W(e^{j\omega})$$

  以矩形窗为例，其频谱为
  

  $$R_N[n]=1,\ n=0,\cdots,N-1\rightarrow W_R(e^{j\omega})=e^{-j\omega\frac{N-1}2}\frac{\sin(\omega N/2)}{\sin(\omega/2)}$$ 其中线性相位部分 $e^{-j\omega\frac{N-1}2}$表示窗函数时延一半长度。不考虑相位特性，只关注其幅度谱，为
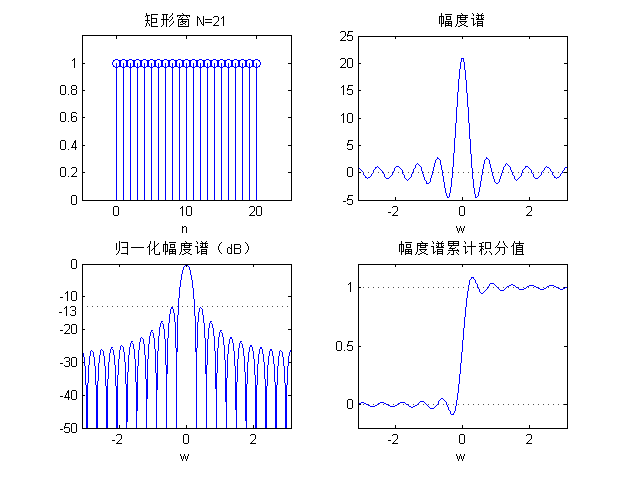
  $$W_R(\omega)=\frac{\sin(\omega N/2)}{\sin(\omega/2)}$$ 对照表1可知， $R_N[n]$偶对称，其幅度谱的特性根据 $N$的奇偶符合第I、II类的情况。其他特性：
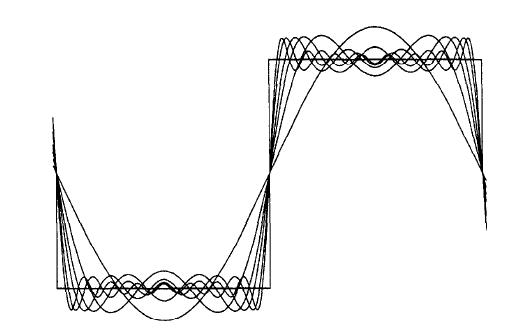
  • 在$\omega=\pm\frac{2\pi}{N}$内有一主瓣，然后向两侧呈衰减震荡展开，主瓣宽度 $\frac{4\pi}{N}$，主瓣峰值 $W_R(0)=N$
    • 在$0\sim\pi$内的零点为$\omega=\frac{2k\pi}{N},k=1,2,\cdots,\lfloor\frac N2\rfloor$，对应旁瓣个数约为$\lfloor\frac N2\rfloor-1$，且旁瓣谱峰是逐渐衰减的
    • $N$越大，主瓣越窄，旁瓣越多，震荡越密集

    图3 矩形窗幅度谱
    

    图4 矩形窗函数效果
    

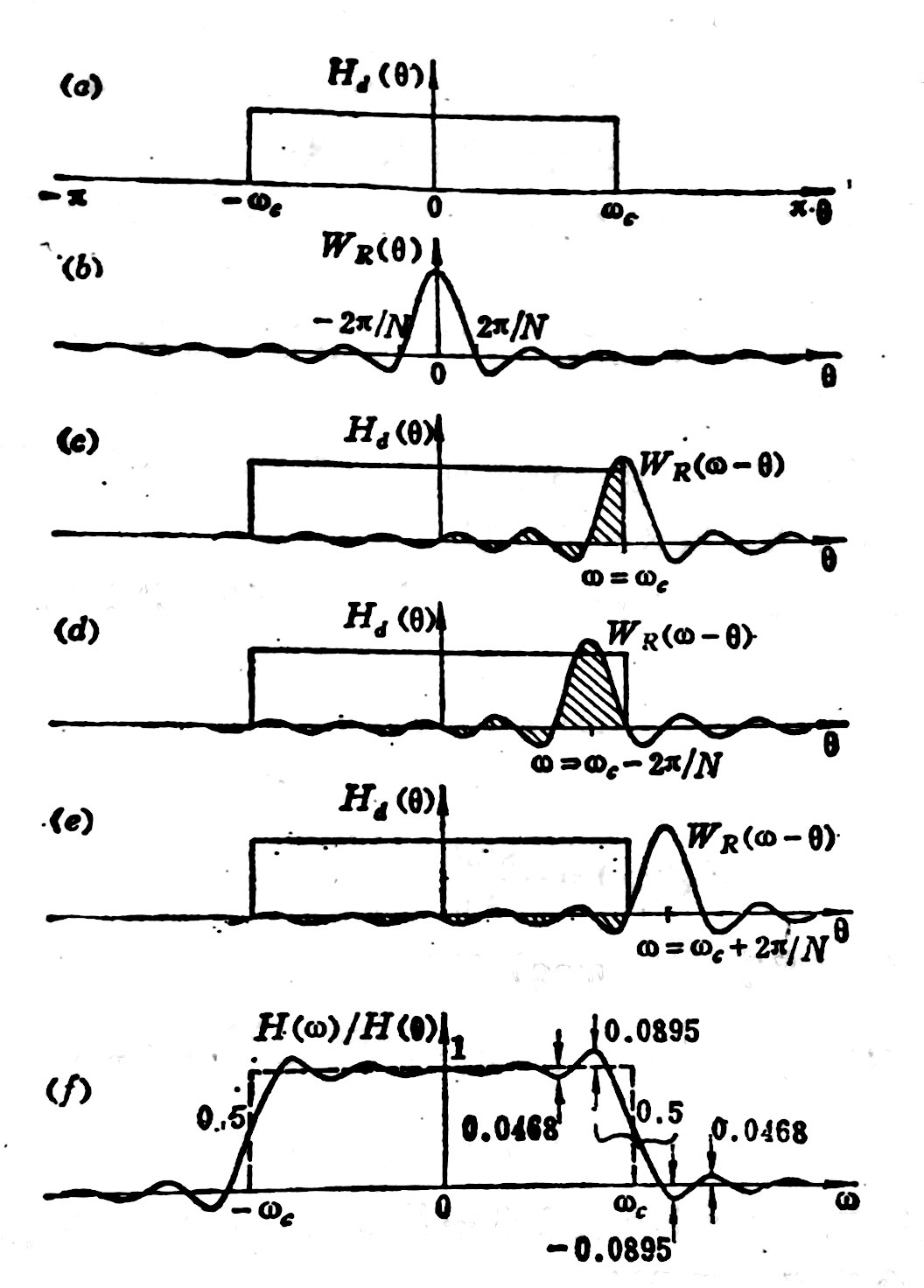
    分析使用矩形窗时的FIR滤波器的幅度谱，
    

    $$H(\omega)=\frac1{2\pi}\int_{-\pi}^{\pi}H_d(\theta) W_R(\omega-\theta)d\theta=\frac1{2\pi}\int_{-\omega_c}^{\omega_c}W_R(\omega-\theta)d\theta=\frac1{2\pi}\int_{\omega-\omega_c}^{\omega+\omega_c}W_R(\theta)d\theta$$
    • $\omega=0$时，$H(0)$等于$W_R(\theta)$在$-\omega_c$到$\omega_c$上的积分，当$\omega_c\gg\frac{2\pi}{N}$时（一般都满足），$H(0)$近似于$W_R(\theta)$在$-\pi$到$\pi$上的全部积分面积，即
      $$H(0)\approx\frac1{2\pi}\int_{-\pi}^{\pi}W_R(\theta)d\theta=R_N[0]=1$$
    • $\omega=\omega_c$时，$H(0)$等于$W_R(\theta)$在0到$2\omega_c$上的积分，近似于$W_R(\theta)$的一半积分面积，即$H(\omega_c)=\frac12H(0)$
    • $\omega=\omega_c-\frac{2\pi}{N}$时，$H(0)$等于$W_R(\theta)$在$-\frac{2\pi}{N}$到$2\omega_c-\frac{2\pi}{N}$上的积分，近似于$W_R(\theta)$的一半积分面积再加上一半主瓣面积。由于此时主瓣全部计算在内，$H(\omega)$达到最大值，出现正肩峰；相反的，$\omega=\omega_c+\frac{2\pi}{N}$时，主瓣全部未计算在内，此时$H(\omega)$达到最小值，出现负肩峰

    因此，可总结出$H(\omega)$的特性：

    • 肩峰：$H(\omega)$在$\omega_c$两旁距离$\frac{2\pi}{N}$处分别出现正负肩峰，肩峰值的大小与主瓣和旁瓣的相对大小有关，取决于窗函数的形状；肩峰值的大小直接影响滤波器通带的平稳和阻带的衰减（通带、阻带容限），应越小越好
    • 过渡带：两肩峰之间形成一个过渡带，其宽度为$\frac{4\pi}{N}$，等于主瓣宽度
    • 通带和阻带内波动：由于旁瓣的影响，当$\omega$由两肩峰处继续朝通带和阻带变化时，形成长长的余震

    在选用窗函数设计FIR滤波器时，应注意：

    • 主瓣宽度尽量窄，以获得较陡的过渡带$\rightarrow$增加窗函数点数
    • 尽量减小旁瓣，使能量集中在主瓣，以减小肩峰，提高阻带衰减$\rightarrow$寻找合适的窗函数

    这里注意一个很奇特的特性：

    • 矩形窗情况下，最大肩峰值始终为0.0895（此时阻带最小衰减为-21dB），与$N$无关——吉布斯（Gibbs）效应，实际上是由于时域截断造成的

    吉布斯（Gibbs）效应

    吉布斯效应：将具有不连续点的周期函数（如矩形脉冲)进行傅立叶级数展开后，选取有限项进行合成。当选取的项数越多，在所合成的波形中出现的峰起越靠近原信号的不连续点。当选取的项数很大时，该峰起值趋于一个常数，大约等于总跳变值的9%。这种现象称为吉布斯效应。

    图5 吉布斯效应
    

    吉布斯效应原始的说法是为了说明，当用傅里叶级数的有限项（有限个频率分量）去逼近信号时，在信号的间断点处会出现一个过渡带以及起伏和超量（肩峰），也就是说频域的截断带来时域的弥散。而且，当所取项数$N$为有限值时，随着$N$的增大，起伏不断向间断点处压缩，但起伏的峰值大小保持不变。同时，$N$增大还有一个好处是，起伏具有的总能量会变小——逼近误差越小。因此，在实际做这样的近似时，应该选择足够大的$N$，以保证这些起伏具有的总能量可以忽略。

    在学傅里叶变换时有一个经典问题：傅里叶变换的基函数——复正弦函数都是平滑的，用复正弦函数的加权和怎么能表示那些有间断点的时间波形如方波？——这也是拉普拉斯最初在审查傅里叶的论文时的一个质疑点。回答是：[5-6]

    • 一方面，可以说拉普拉斯是对的，用一系列正弦波的线性组合无法精确描述那些具有间断点的信号。根据吉布斯现象，当正弦波数量增多时，超量始终存在，且幅值保持稳定约为9%，只是超量的宽度变小并向间断点压缩。
    • 另一方面，用一系列正弦波的线性组合可以无限逼近那些具有间断点的信号，以至逼近误差的能量为0。当正弦波数量无限多时，超量依然存在，但其宽度为0，因此在能量意义上为0。更精确地，间断点处的值收敛于信号在该跳跃点两侧值的均值。可以证明，傅里叶级数表示是收敛的，其逼近误差的能量为0。基于此，傅立叶是对的。

    回到本文，在用窗函数法设计FIR滤波器时，实际遇到的是与上面相反的吉布斯现象——时域的截断带来频域的弥散，即用窗函数去截断理想滤波器的单位脉冲响应时，对应的FIR滤波器的幅度谱在截止频率处会出现过渡带以及起伏和肩峰。

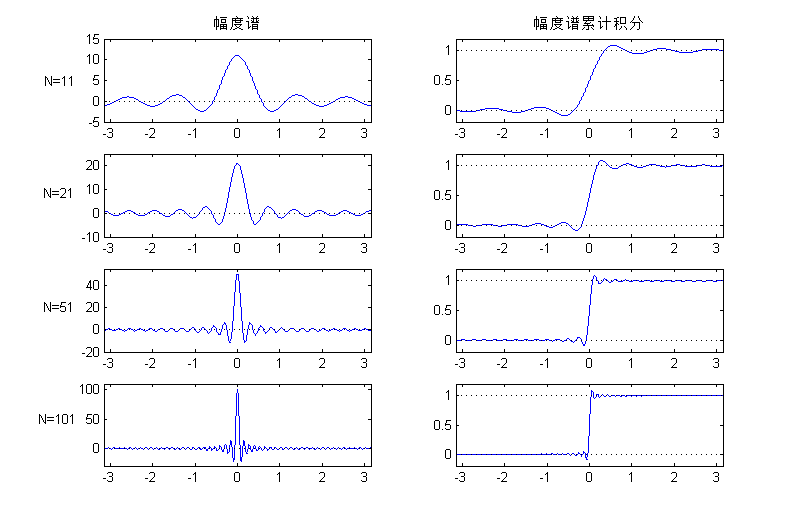
    一开始纠结了好半天这个0.0895或是这个9%是怎么算出来的，直接手算推导失效，最后只好借助于强大的MatLab了。这里可借助于矩形窗幅度谱$W_R(\omega)$的特性来解释吉布斯效应。上面讲到，$N$的增大可以使主瓣变窄$\rightarrow$过渡带变窄，同时旁瓣增多，震荡变密集$\rightarrow$通带和阻带内震动加快，但并不能改变肩峰值和波动的相对大小（主瓣与旁瓣的相对比例）。

    首先从幅值上简单分析，主瓣峰值$W_R(0)=N$，第一旁瓣峰值大约在$\frac{3\pi}{N}$处取得，有
    

    $$|W_R(\frac{3\pi}{N})|=|\frac{\sin\frac{3\pi}2}{\sin\frac{3\pi}{2N}}|\approx \frac{2N}{3\pi}\approx 0.212N$$ 关于$N$做归一化后，第一旁瓣峰值对应于13dB衰减处，如图3。也就是说主瓣与旁瓣的相对大小是固定的。

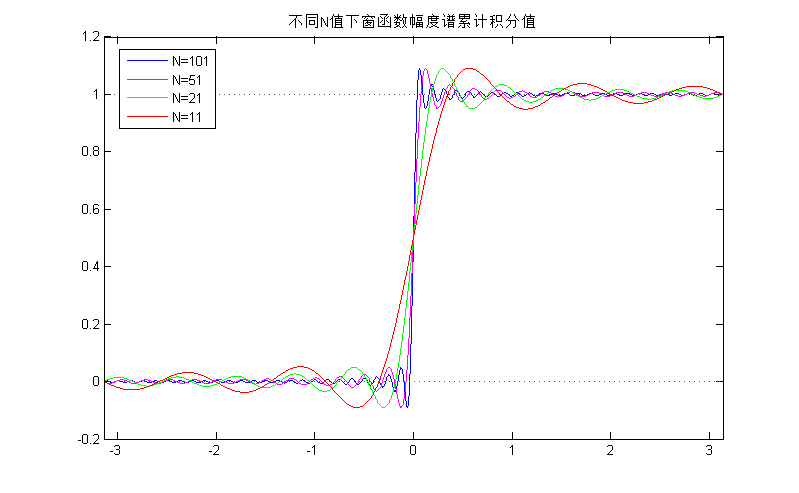
    做出不同$N$值下矩形窗幅度谱的累计积分曲线，可知其肩峰值稳定在0.09附近，如图6、7。同时，计算波动所具有的总能量，这里计算图6中左半边波形所具有的总能量，在$N=11、21、51、101$时分别为28.85、15.11、6.22、3.12，确实随着 N <script type="math/tex" id="MathJax-Element-148">N</script>的增大而减小。

    图6 不同长度矩形窗的幅度谱
    

    图7 不同长度矩形窗的幅度谱累计积分
    

    以上。下篇讨论窗函数。

    ---

    参考

    1. Low Cut Filter http://helpguide.sony.net/icd/sx3/v1/cs2/contents/TP0000020730.html
    2. 滤波器设计指标 http://helpguide.sony.net/icd/sx3/v1/cs2/contents/TP0000020730.html
    3. 邹理和《数字信号处理（上册）》
    4. 傅立叶变换中的吉布斯现象 http://blog.csdn.net/deepdsp/article/details/7406251
    5. 为什么要进行傅立叶变换 http://blog.csdn.net/xfortius/article/details/8912488
    6. Steven W. Smith The Scientist and Engineer’s Guide to Digital Signal Processing : Chapter 8&11 http://www.dspguide.com/pdfbook.htm