总结一下最短路径的弗洛伊德算法（Floyd）

看了好多大牛博客，我把弗洛伊德算法在这里总结一下。

弗洛伊德算法的介绍，先参考百度百科：Floyd算法

再来几篇可以参考的博文：http://www.wutianqi.com/?p=1903

http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html

--------------------------------------------------------------------分割线-------------------------------------------------------------------------------------------------------------

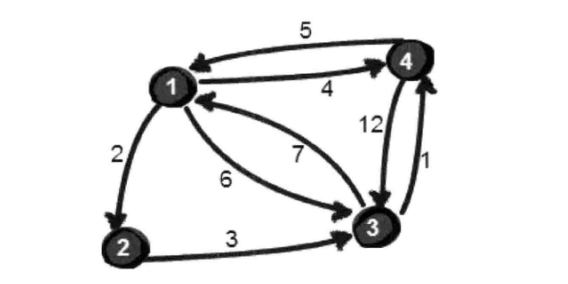
现在我们有这么一张图：

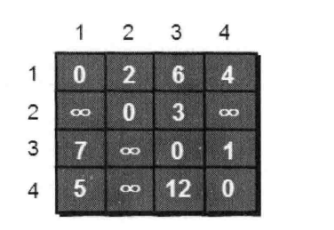
我们要做的是求出从某一点到达任意一点的最短距离，我们先用邻接矩阵来建图，map[i][j]表示从i点到j点的距离，把自己到自己设为0，把自己到不了的边初始化为无穷大，代码为：

//初始化
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(i==j)
                map[i][j]=0;
            else
                map[i][j]=inf;
    //读入边
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d%d",&t1,&t2,&t3);
        map[t1][t2]=t3;
    }

最后，建好的图可以用表格来表示：

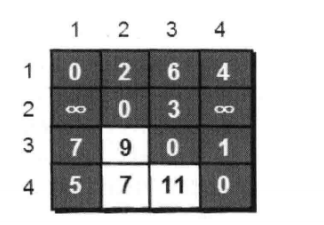
现在，我们来思考，假设我们来找一个中转的点，看他们的路程会不会改变，我们先以1号顶点作为中转点最为例子，制图：

我们发现，图有了变化，我们怎么判断以1号顶点作为中转点图的路程是不是更短呢，我们只需要判断map[i][1]+map[1][j]的路程是不是比map[i][j]的路程更短，就可以判断，

代码为：

for(int i=1; i<=n; i++)
    for(int j=1; j<=n; j++)
        if(map[i][1]+map[1][j]<map[i][j])
            map[i][j]=map[i][1]+map[1][j];

现在该怎么办呢，我们接着以2号顶点作为中转点，很简单代码修改一句就就可以：

for(int i=1; i<=n; i++)
    for(int j=1; j<=n; j++)
        if(map[i][2]+map[2][j]<map[i][j])
            map[i][j]=map[i][2]+map[2][j];

现在我们是不是发现了一个规律，只要不断的遍历每一个点，并且以每一个点作为中转点看看它的值会不会改变，就可以得到从一个点到任意一个点的最短路径，也就是多源最短路，这就是弗洛伊德算法，代码为：

for(int k=1; k<=n; k++)
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(map[i][k]+map[k][j]<map[i][j])
                map[i][j]=map[i][k]+map[k][j];

这样就可以遍历每个顶点，找出所有的最短路，算法的复杂度为O(n^3).

对于我一开始提出的问题，完整的代码为：

#include <stdio.h>
#include <string.h>
#include <string>
#include <iostream>
#include <stack>
#include <queue>
#include <vector>
#include <algorithm>
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int inf=1<<29;
int main()
{
    int map[10][10],n,m,t1,t2,t3;
    scanf("%d%d",&n,&m);//n表示顶点个数，m表示边的条数
    //初始化
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(i==j)
                map[i][j]=0;
            else
                map[i][j]=inf;
    //读入边
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d%d",&t1,&t2,&t3);
        map[t1][t2]=t3;
    }
    //弗洛伊德(Floyd)核心语句
    for(int k=1; k<=n; k++)
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                if(map[i][k]+map[k][j]<map[i][j])
                    map[i][j]=map[i][k]+map[k][j];
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
            printf("%10d",map[i][j]);
        printf("\n");
    }
    return 0;
}

给出样例：

输入：

4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12

输出：

         0         2         5         4
         9         0         3         4
         6         8         0         1
         5         7        10         0

输出的就是我建图的时候用的表格，可以表示任意一点到任意一点的最短距离。
如果有什么不对的地方，欢迎指正~~