DynamicFusion：如何将KinectFusion算法扩展到动态的三维重建场景

本文对DynamicFusion[1]做个简介，注意需要结合笔者上一篇关于KinectFusion的文章共同食用[5]。如有错误，欢迎评论指正。

---

一.算法流程

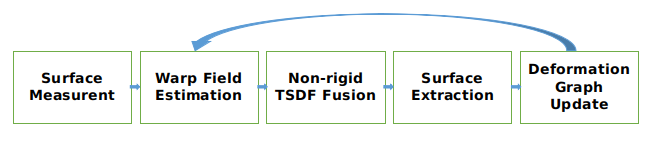
图1.算法流程

相比于KinectFusion，DynamicFusion[1]最大的区别在于引入了Deformation Graph[2]，通过Warp Field（包括对应于相机运动的刚性变换，和对应于物体形变的非刚性变换）将Canonicial空间的model变换到Camera空间的frame，从而实现对待重建的动态物体的TSDF场进行更新，最终完成重建。下文着重对与KinectFusion不同的部分做下描述。

二.具体步骤

1.Surface Measurent

与KinectFusion一致，对输入深度图进行金字塔下采样，双边滤波、转点云、计算法线等操作。

2.Warp Field Estimation

1）估计刚性变换矩阵

与KinectFusion一致，采用point2plane icp估计刚性变换矩阵 [3]。此时，源点云为施加了当前估计的Warp Field的Canonicial模型（下一步会介绍）渲染得到的深度图转换得到，目标点云即为当前live frame。

• 注：
  1）不是和下面非刚性变换一起解优化问题同时求得的;
  2）施加了Warp Field后的Canonicial模型就是点云，为什么还要渲染成深度图，然后再转成点云？据我所知，应该是为了能够用投影法找对应点对，这样比直接搜索两个点云之间的对应点对要快得多，同时也能够复用KinectFusion的代码。

2）估计对应点对

对Canonicial模型中的每个点 ，施加Warp Field定义的变化 ，将其变换到live frame上：

式1

式2

式3

式4

式5

• 注：
  1）即为上一步估计的刚性变换（注意此时已经更新了，不是第一步施加Warp Field时的刚性变换了），而 为非刚性变换；
  2）Warp Field其实就是由一组在Canonicial模型上稀疏采样(常用最远点采样)得到的结点构成，每个结点包含位置、权重、变换矩阵（采用对偶四范数的表示，便于非线性优化； 表示将其转换成我们常见的3x3或者4x4的欧式变换矩阵）三个变量：

3）对于Canonicial模型上的每个点及其法线 ，利用其k近邻或r半径内的结点，根据式2计算结点的加权平均变换（式2），然后将这个变换施加上去（式4，式5），即可变换到live frame空间。

接下来就和KinectFusion一致了，由于现在Canonicial模型和live frame处于同一空间，我们可以将Canonicial投影到像素空间上，然后在某个小范围（比如3x3邻域）内根据设定的法线夹角阈值，筛选得到对应点对，用于下面非线性最小二乘问题的优化。

3）求解非线性最小二乘优化问题

待优化目标函数如式6、7、8所示。原论文花了大篇幅介绍如何利用高斯牛顿法对上面问题式7的求解，也提及了可用PCG算法进行加速求解。

式6

式7

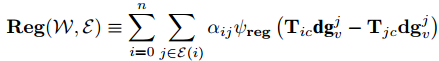
式8

• 注：
  1）包含数据项式7和正则项式8，与Deformation Graph一致（指的是误差项是一致的，实际具体构造不太一样：Embeding graph里面每个顶点的更新公式不是像式4这样的加权平均变换得到；Embeding graph采用的变换矩阵是原始的3x3或者4x4的矩阵，所以需要对其额外进行约束）[2]；
  2）正则项里面涉及到节点之间的连接关系，应该就是利用k近邻或者r半径范围内近邻构建的；

3.Non-rigid TSDF Fusion

1）投影

首先对Canonicial空间TSDF场的每个体素中心，同样按照式7将其变换到live frame空间中得到 。

2）更新TSDF

然后按以下公式更新Tsdf场

式9

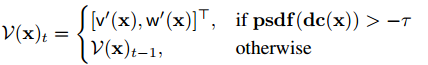
式10

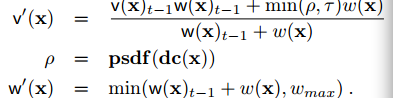
式11

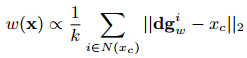
式12

• 注：
  1）式9，为利用相机参数将投影到像素空间上的位置，据此得到在live frame上得到对应的点，然后和做差得到psdf值；
  2）根据式10、式11、式12更新Tsdf场，其中为当前体素的Tsdf值，为当前体素的权重值。

4.Surface Extraction

与KinectFusion一致，利用Marching Cube算法提取网格（当前已重建的模型），或者利用Raycast算法提取点云（当前视角下的点云）。

5.Deformation Graph Update

1）计算新结点

对于更新后的Canonical模型上的每个点 ，利用当前节点 ，由下式计算筛选得到非支持点，对非支持点进行采样得到待插入的deformation graph上的新结点

式13

• 注：
  论文中提及是用simple radius search averaging的方法进行采样得到新结点。

2）计算新结点变换矩阵，并更新整个结点图

根据式14，也就是待插入结点邻域范围内的已有结点的变换矩阵的加权平均，作为待插入结点变换矩阵的初始值.

式14

式15

• 注：
  这块作者提到了hierarchical deformation tree，不确定意思是不是和金字塔图像一样，指的是较高层的结点是由较低层采样得到的（存疑，欢迎评论指教）。

三.开源实现

笔者目前只推荐[4]中的实现，因为其最为完整，并且提供了求解上面非线性最小二乘问题所需的Jacobi矩阵的详细推导。

四.参考

[1]Richard A Newcombe, Dieter Fox, and Steven M Seitz. Dynamicfusion: Reconstruction and tracking of nonrigid scenes in real-time. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 343–352, 2015
[2]R. W. Sumner, J. Schmid, and M. Pauly. Embedded deformation for shape manipulation. ACM Trans. Graph., 26(3):80,2007
[3]Low, Kok-Lim. "Linear least-squares optimization for point-to-plane icp surface registration."Chapel Hill, University of North Carolina4.10 (2004): 1-3
[4]https://github.com/dolphin-li/DynamicFusion
[5]https://mp.weixin.qq.com/s?__biz=MzI4OTkwODM3NQ==&mid=2247484251&idx=1&sn=bf94e3f027d38055913cf5ec0513e00e&chksm=ec26b0a3db5139b51a880c5851d0cb1aee246004b2bdc0326272d557ba6c5738d9b31bdde907&token=1098252562&lang=zh_CN#rd