多元线性回归算法: 线性回归Linear Regression、岭回归Ridge regression、Lasso回归、主成分回归PCR、偏最小二乘PLS

0. 问题描述

输入数据：$\mathbf{X}=(x_1,x_2,....,x_m)$, 相应标签 $\mathbf{Y}=(y_1,y_2,...,y_m)$.

目标：建立模型描述$X$ 和 $Y$ 的关系。

1. 线性回归，LR

模型：
$$Y=wX+b$$

使用平方误差作为模型损失函数：
$$L=\sum _{i=1}^m(y_i-x_i^{T}w)$$

矩阵表示：
$$L=(y-Xw{)}^T(y-Xw)$$

求解：

对w求导，得到：
$$\hat{w}=(X^{T}X{)}^{-1}{X}^{T}y$$

2. 局部加权线性回归，LWLR

英文名称为：Locally Weighted Linear Regression.

在线性回归的基础上，引入一些偏差，从而降低预测的误差。

对预测的样本点赋予一定的权重。
LWLR使用“核”来对附近的点赋予更高的权重，常用高斯核：
$$w(i,i)=exp(\frac{|x^{(i)}-x|}{-2k^2})$$
k 为超参数。

模型损失函数

$$\begin{array}{rl}\mathcal{L}& =\frac{1}{2}\left[W^{(1)}{\left(y^{(1)}-{\mathbf{\theta }}^T{\mathbf{x}}^{(1)}\right)}^2+W^{(2)}{\left(y^{(2)}-{\mathbf{\theta }}^T{\mathbf{x}}^{(2)}\right)}^2+\cdots +W^{(m)}{\left(y^{(m)}-{\mathbf{\theta }}^T{\mathbf{x}}^{(m)}\right)}^2\right]\\ & =\frac{1}{2}\sum _{i=1}^m{W}^{(i)}{\left(y^{(i)}-{\mathbf{\theta }}^T{\mathbf{x}}^{(i)}\right)}^2\end{array}$$

其中，$\mathbf{\theta }=(w,b)$

求解的w :

$$\hat{w}=(X^{T}WX{)}^{-1}{X}^{T}Wy$$

---

当数据的特征比样本点多时， 计算$(X^{T}X)$为非满秩矩阵，求逆会出错。岭回归和Lasso回归都是解决这个问题

3. 岭回归Ridge regression

岭回归让$(X^{T}X)$加上$\lambda I$来使得矩阵非奇异。

回归系数变成：
$$\hat{w}=(X^{T}X+\lambda I{)}^{-1}{X}^{T}y$$

而其本质上，则是求解这个最优化问题：

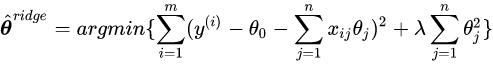
其中，$\mathbf{\theta }=w$

注意到右侧添加了一个L2范数惩罚项。L2范数使得 $\theta$ 的各分量不会过大(防止模型过拟合、降低模型复杂度)，起到一个收缩作用；

岭回归一开始用来处理特征数比样本数多的情况，现在通过引入$\lambda$来限制所有 w之和，通过加入该惩罚项来减少不重要的参数，在统计学叫缩减（shrinkage）。

4. Lasso 回归

Lasso回归使用 1 范数对 w 进行约束，约束条件为：

$$\sum _{k=1}^n|w_k|\le \lambda$$

当λ很小的时候，一些系数会随着变为0，而岭回归却很难使得某个系数恰好缩减为0， Lasso容易获得稀疏解。

岭回归与Lasso回归异同

相同：
都可以用来解决标准线性回归的过拟合问题。

不同：

lasso 可以用来做特征选择，而 ridge 不行。或者说，lasso 更容易使得权重变为 0，而 ridge 更容易使得权重接近 0。
从贝叶斯角度看，lasso（L1 正则）等价于参数 w 的先验概率分布满足拉普拉斯分布，而 ridge（L2 正则）等价于参数 w 的先验概率分布满足高斯分布。

---

5. 主成分回归PCR

主成分回归分为两步，1是测定主成分数，幷由主成分分析（PCA）将矩阵X降维；2是降维的X矩阵再进行线性回归分析。

主成分是指，有原向量线性组合成的一个新向量，它用来表征原来变量时所产生的平方误差最小。

运用主成分分析，原变量矩阵 X 可表达成得分（即主成分）矩阵T，T由X在本征矢量 P 上的投影所得。

$$T=XP$$

多元线性回归应用了由 X 的列定义的全部空间，而主成分回归所占用的是一子空间。

$$\begin{array}{c}T=XP\\ Y=TB+E\end{array}$$
其中，解：
$$B={\left(T^{\prime }T\right)}^{-1}{T}^{\prime }Y$$
主成分分析可以解决共线问题，去掉不太重要的主成分，减少随机误差产生的影响。

6. 偏最小二乘回归PLS

英文名：parital least squares.
PLS应用广泛的原因有：
-1. 模型的预报残差平方和较小。与线性回归，主成分回归等相比，具有较高的预报稳定性。
-2. PLS方法适合用于处理变量多而样本数又少的问题，高效地抽取信息。

原理：
输入矩阵 X, 目标矩阵Y，普通最小二乘法建立以下线性模型：
$$Y=XB+E$$
其中，B为回归系数矩阵，E为残差矩阵，并且：
$$B=(X^{T}X{)}^{-1}{X}^{T}Y$$

• PLS 方法首先将矩阵 X 作双线性分解，即，
  $$X=TP+E(1)$$
  其中，矩阵 T 含有两两正交的隐变量或得分矢量 t .
• PLS 方法与主成分分析法不相同之处在于，主成分分析法要求分解后得到 t 的隐变量的方差最大。 PLS方法，需要用到矩阵 Y的信息，矩阵Y 也作双线性分解，即
  $$Y=UQ+F(2)$$

其中，U矩阵包涵 Y 的隐变量 u,即 u 为矩阵Y中变量的线性组合， F 为残差阵。

• PLS要求X分解得到的隐变量t与Y分解得到的隐变量u为最大重叠或相关性最大，因此，
  $$u=vt+e.$$
  其中，e 为残差矢量，系数根据最小二乘确定。

求解：
求解方法一：
（1）将 X 标准化并记为$E_0={\left(E_{01},E_{02},\dots ,E_{0P}\right)}_{n\times p}$，Y 标准化并记为$F_0={\left(F_{01},F_{02},\dots ,F_{0q}\right)}_{n\times q}$

（2）记 $t_1$ 是 $E_0$ 的第一个成分，$t_1=E_0{w}_1$，$w_1$是$E_0$的第一个轴，它是一个单位向量，即 $||w_1||=1$.
（3）为了$t_1$,$u_1$能分别代表 X, Y中的变异信息，以及要求 $t_1$ 对 $u_1$ 有最大的解释能力，即 $t_1$,$u_1$的相关度达到最大值，即
$$\begin{gathered} maxvar(t_1） \\ maxvar(u_1) \\ maxr(t_1,u_1) \end{gathered}$$
综合起来，就是协方差最大，
$$maxCov(t_1,u_1)=\sqrt{var(t_1)}\sqrt{var(u_1)}r(t_1,u_1)$$

正规的表达式：

$$\begin{array}{l}\max <E_0{w}_1,F_0{c}_1>\\ \text{s.t}\left\{\begin{array}{l}{w}_1^T{w}_1=1\\ c_1^T{c}_1=1\end{array}\right\}\end{array}$$

在${\Vert w_1\Vert }^2=1$ 和 ${\Vert c_1\Vert }^2=1$ 的约束条件下，求 $w_1^T{E}_0^T{F}_0{c}_1$ 最大值。
采用拉格朗日算法，记

$s=w_1^T{E}_0^T{F}_0{c}_1-{\lambda }_1\left(w_1^T{w}_1-1\right)-{\lambda }_2\left(c_1^T{c}_1-1\right)$

求偏导，有
$$\begin{array}{rl}& \frac{\partial s}{\partial w_1}=E_{\mathrm{o}}^T{F}_{\mathrm{o}}{c}_1-2{\lambda }_1{w}_1=0\\ & \frac{\partial s}{\partial c_1}=F_0^T{E}_0{w}_1-2{\lambda }_2{c}_1=0\\ & \frac{\partial s}{\partial {\lambda }_1}=-\left(w_1^T{w}_1-1\right)=0\\ & \frac{\partial s}{\partial {\lambda }_2}=-\left(c_1^T{c}_1-1\right)=0\end{array}$$

推出，$$\begin{array}{rl}& 2{\lambda }_1=2{\lambda }_2=w_1^T{E}_0^T{F}_0{c}_1=c_1^T{F}_0^T{E}_0{w}_1=<E_0{w}_1,F_0{c}_1>\end{array}$$

记${\theta }_1=2{\lambda }_1$,
则， ${\theta }_1$是优化问题的目标函数值。

并且有：
$$\begin{gathered} E_0^T{F}_0{F}_0^T{E}_0{w}_1={\theta }_1^2{w}_1 \\ {F}_0^T{E}_0{E}_0^T{F}_0{c}_1={\theta }_1^2{c}_1 \end{gathered}$$
可见，$w_1$ 是矩阵$E_0^T{F}_0{F}_0^T{E}_0$ 的特征向量，对应的特征值为${\theta }_1^2$. ${\theta }_1^2$是目标函数值，要求取最大值，所以，$w_1$ 是对应$E_0^T{F}_0{F}_0^T{E}_0$矩阵最大特征值${\theta }_1^2$的单位特征向量。
同理，$c_1$ 是对应$F_0^T{E}_0{E}_0^T{F}_0$矩阵最大特征值${\theta }_1^2$的单位特征向量。
（4）求取$w_1$，$c_1$ ，得到成分，

$$\begin{array}{rl}& t_1=E_0{w}_1\\ & u_1=F_0{c}_1\end{array}$$
（5）分别求$E_0,F_0$对$t_1,u_1$的3个回归方程。

$$\begin{array}{rl}& E_{\mathrm{o}}=t_1{p}_1^T+E_1\\ & F_0=u_1{q}_1^T+F_1^{\ast }\\ & F_{\mathrm{o}}=t_1{r}_1^T+F_1\end{array}$$
其中，回归系数向量是，
$$\begin{array}{rl}& p_1=\frac{E_0^T{t}_1}{{\Vert t_1\Vert }^2}\\ & q_1=\frac{F_0^T{u}_1}{{\Vert u_1\Vert }^2}\\ & r_1=\frac{F_0^T{t}_1}{{\Vert t_1\Vert }^2}\end{array}$$
其中，$E_1{F}_1^{\ast }{F}_1$是3个回归方程的残差矩阵。

（6）用残差矩阵$E_1,F_1$取代$E_0,F_0$，然后求第2个轴$w_2,c_2$以及第2个成分$t_2,u_2$。

$$\begin{array}{rl}& t_2=E_1{w}_2\\ & u_2=F_1{c}_2\\ & {\theta }_2=<t_2,u_2>=w_2^T{E}_1^T{F}_1{c}_2\end{array}$$

不断计算下去。
（7）如果 X 的秩是A，则有：
$$\begin{array}{rl}& E_0=t_1{p}_1^T+t_2{p}_2^T+\dots +t_A{p}_A^T\\ & F_0=t_1{r}_1^T+t_2{r}_2^T+\dots +t_A{r}_A^T+F_A\end{array}$$

PLS 和PCA的比较：

---

最近开通了个公众号，主要分享机器学习相关内容，推荐系统，风控等算法相关的内容，感兴趣的伙伴可以关注下。

公众号相关的学习资料会上传到QQ群596506387，欢迎关注。

---

参考：

1. PCA回归实现myself；
2. 多元线性回归 文库；
3. 多元线性回归中多重共线性问题的解决办法探讨_张凤莲.caj;
4. 【机器学习-回归】岭回归与Lasso回归;
5. 机器学习 - 局部加权线性回归;
6. 机器学习算法实践-岭回归和LASSO;
7. 线性回归——lasso回归和岭回归（ridge regression）;