博弈论简述 第三章 不完全信息静态博弈

一、不完全信息静态博弈和贝叶斯纳什均衡

1.1不完全信息博弈

完全信息：收益函数是共同知识。参与者对其他参与人策略空间、行动特征以及收益完全了解。完全信息自然不首先行动（或自然行动被所有参与人准确观察），也就是没有事先的不确定性.

不完全信息： 至少有一个 人不能确定其他人的收益函数

不完全信息博弈：

（1）收益函数依赖于自然的选择（外部环境）

例：在房地产商开发博弈中，若市场需求是不确定的，即为一不完全信息博弈。

分析：

p＞1/3时，（开发，开发）是占优均衡；

p≤1/3时，纯策略纳什均衡：（开发，不开发）和（不开发，开发）；混合策略纳什均衡：双方都以(1+3p)/2的概率选择开发。

（2）A的收益函数是B私人信息的函数，也就是说A的收益与B有关（内部对手）

例：市场进入博弈模型

        1）完全信息博弈

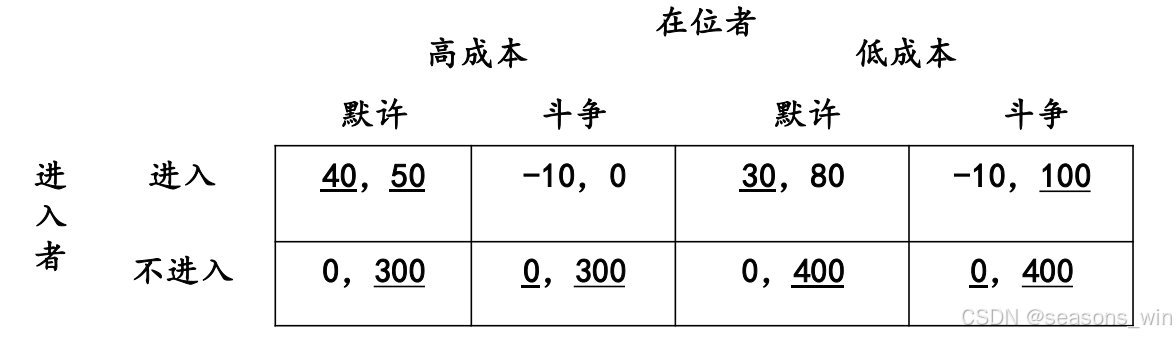
分析：

完全信息，所以进入者知道在位者的收益。

高成本：纯策略纳什均衡（进入、默许），（不进入、斗争）；

低成本：纯策略纳什均衡（不进入、斗争）。

        2）不完全信息博弈： 若在位者：高成本：p，低成本：1-p（概率）

分析：

选择进入的期望利润为： 40p+(-10)(1-p)= 50p-10（解释：当进入者选择进入时，在位者在高成时会选择默认，低成本时选择斗争）

选择不进入的期望利润为：0

因此，潜在进入者的最优选择是：若