GAMES101(7~10.5节，着色，插值，渲染流水线，纹理映射和贴图）

Shading着色

光线传播越远，强度越小

冯氏光照 / Blinn-Phong着色模型：

环境光（常量）：颜色 * 强度

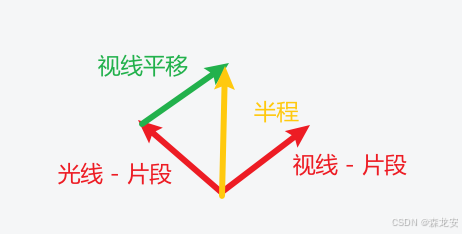
法线n，观测方向v，光照方向I，反射光线R，半程向量H（V和I的角平分线）光泽度shininess，自身颜色color

//

漫反射

两个性质：

能量守恒（决定到达的能量）：

求半程

1. 光的传播过程中，总能量保持不变，反射的能量不能超过入射的能量
2. 入射光的能量等于反射光和折射光的总能量

余弦定理（决定接受的能量）：I与n夹角越大，物体表面接受的光照总量越小，即点乘结果

镜面反射

漫反射：kd为本身的颜色 * 到达能量 * 吸收的比率

//

R和V夹角越近，颜色强度越大，等价于，H和n的夹角

指数P

半程向量 = I + V / || I + V || 归一化（仅方向）

指数p：比如没有指数，在比如45的角度下看平面，会看到比较大的高光区域，因为cos值仍比较大，因为对于很多点都有比较亮的高光

线性插值，v0=0,v1=1,x:0--1

镜面：ks为高光的颜色（通常为白色） * 到达能量 * 看到高光的比率，指数p（通常为100~200）

插值

重心插值

插值：已知顶点之间估算中间数据值的过程，插值的目的是通过已知顶点的属性，计算出多边形内部任意位置的属性值，从而平滑的过渡效果。

插值类型

1·线性插值：它根据片段距离每个顶点的比例来插值数据。

重心坐标

2·重心插值：用于表示一个点 P 在三角形内部的相对位置，对于三角形平面任意一点，都可以表示为3个顶点的线性形式，如果在三角形内，abc的权重都>0 。根据三角形面积求点对应的重心坐标（barycentric coordinates）abc的权重。

三角形重心：重心坐标为1/3，1/3，1/3 ，相加满足和为1的性质

如何计算每个三角形面积？

根据计算三角形面积比求出的重心坐标

通过重心坐标可以求出内部的点对于三角形顶点的，颜色，深度，法线，纹理等属性插值结果

透视校正：在3D场景中，由于投影变换的存在，单纯的线性插值可能导致错误的结果。比如深度，在透视投影中，z的变换是非线性的（近大远小），

应该首先获取像素逆变换到3维空间的坐标，在3维空间通过重心插值获取属性，再把值应用到像素上

理解框架中深度z插值：

//计算坐标在三角形的重心坐标
static std::tuple<float, float, float> computeBarycentric2D(float x, float y, const Vector3f* v)
{
    float c1 = (x*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*y + v[1].x()*v[2].y() - v[2].x()*v[1].y()) /
     (v[0].x()*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*v[0].y() + v[1].x()*v[2].y() - v[2].x()*v[1].y());
    float c2 = (x*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*y + v[2].x()*v[0].y() - v[0].x()*v[2].y()) /
     (v[1].x()*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*v[1].y() + v[2].x()*v[0].y() - v[0].x()*v[2].y());
    float c3 = (x*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*y + v[0].x()*v[1].y() - v[1].x()*v[0].y()) /
     (v[2].x()*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*v[2].y() + v[0].x()*v[1].y() - v[1].x()*v[0].y());
    return {c1,c2,c3};
}
// 根据重心坐标计算坐标最终的z深度
std::tie(alpha, beta, gamma) = computeBarycentric2D(i+a[k], j+a[k+1], t.v);
//透视校正
float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;

3种着色方式： 

Face Flat平面着色：对每个三角形四边形有相同的法线，法线根据三角形边两个两个插值得到，因此每个三角形内部有完全一致的结果

Vertex Gouraud顶点着色：对每个顶点着色，内部用插值计算颜色，结果近似

Pixel Phong像素着色：着色应用在每个像素上，法线方向在内部插值，有更精确的结果

//

法线插值：

比如某顶点是周围三角形的公有顶点，求这个顶点的法线，就是其他的三角形法线方向的加权平均值

渲染流水线

渲染流水线：

将 3D 场景 转换为 2D 图像的过程

• 渲染流水线（Rendering Pipeline）：侧重于 GPU 内部的处理阶段，尤其是渲染的各个阶段如何协作从 3D 数据生成图像。更具技术细节，描述数据如何在 GPU 上流动。

• 渲染管线（Render Pipeline）：是一个更宽泛的概念，涵盖了从场景数据组织到图形渲染的全流程，包括 CPU 端的场景管理、资源调度、API 调用以及 GPU 的流水线处理。

• 图形管线（Graphics Pipeline）：主要描述图形 API（如 OpenGL、Vulkan 等）如何控制 GPU 渲染阶段。更注重图形 API 的设计和其对 GPU 的控制流程。

Shader：

是渲染流水线中可编程的部分，

和作业框架不同，使用图形api时，对于顶点或片段的操作应写在shader中，对于opengl来说需要用glsl语言，directx需要hlsl语言……

当bind绑定shader并调用drawcall时，会自动（非for循环）对每个顶点计算位置和片段/像素计算颜色，运行绑定的着色器

• 顶点着色器（Vertex Shader）：处理每个顶点的输入，计算坐标变换、法线变换、纹理坐标等。

• 片段着色器（Fragment Shader）：处理光栅化后每个像素（片段）的颜色、纹理映射、光照计算等。

• 几何着色器（Geometry Shader）：可选阶段，用于在顶点之后、光栅化之前对几何体进行修改。

• 计算着色器（Compute Shader）：独立于渲染流水线，可以用于并行处理复杂计算任务，比如物理模拟、流体模拟等。

GPU：

执行渲染流水线，并以极高的效率并行执行流水线中的任务。

纹理映射

基本概念

纹理：一块有分辨率的缓冲（内存），可以保存到立方体或球体（展开有问题）等，它不仅可以保存颜色信息，也可以保存其他数据

纹理坐标UV：每个顶点指定对应的纹理uv坐标，从而获取uv对应的纹理颜色，作为着色模型kd系数

纹理插值：对于内部的点，也需要找到对应的uv坐标

因为纹理有分辨率，每个像素又叫做纹素

//

纹理走样问题： 无论纹理分辨率过高（远处（Moire））还是过低都会产生走样

bilinear插值

4*4分辨率，临近插值

分辨率过低产生锯齿

分辨率过高，产生波纹状或闪烁

分辨率过低

纹理插值方式（点查询）：

UV分辨率过高

nearest临近插值：如果纹理分辨率不足，很多像素（透视校正结果）投影到非整数的uv坐标，取整后对应同一个纹素，就会形成明显的锯齿状

bilinear双线性插值：取周围4个坐标，水平竖直方插值

bilinear三线性插值：取周围16个坐标，水平竖直方向插值

分辨率过高

思路就是查询像素对应的uv纹理范围，求均值，那么如何得知对应的范围以及均值呢？

0~7级别，分辨率逐渐降低

解决方式：

增加采样点（比如一个像素512个采样点，但是太消耗性能）求平均值

Mipmap（多级渐远纹理）（仅能查询正方形）：近似的较快的正方形查询算法，并且解决透视投影uv范围不同

Mipmap查询

  

临近点：首先查询像素本身和邻居对应的uv坐标，通过距离近似的方式，采样uv正方形，

如何查询？正方形在不同级别对应一个或多个或小于一个的纹素，查找对应一个纹素的mipmap，从而一次查询结果

优化：

但是层级有限，会出现断层，需要通过三线性插值解决突然断层问题，在两个层分别双线性插值，在对两个层线性插值

问题：

但是三线性插值存在一些问题，并不能针对所有uv范围的形状

Ripmap 各项异性过滤（矩形/正方形），它不必仅查询正方形，用矩形做过度，对于矩形的纹理查询效果较好

EWA过滤：对于纹理中不规律的形状查询

当分辨率一致

精度问题

依旧会出现走样问题：

比如渲染阴影时通常深度贴图和屏幕分辨率一致，依旧出现条纹的失真，本质依旧是分辨率问题：虽然都是一定范围区域投影到同一个屏幕像素，但是光的视角和摄像机视角不同，

因此，假设每个像素采样一次（一个采样点在像素中心），光的视角下渲染，像素被更新为采样点逆变换到3d空间对应的深度值，

而摄像机视角可能像素采样点对应的并非和光的那个一致，比如在采样点前方或后方，却从同一深度贴图的像素采样，得到的是不同的结果

透视的影响

直观每个像素对应的uv范围，近处的对应范围少，远处对应范围多，因此会有较大的偏差，应该范围采样解决走样，相当于求范围的均值

纹理贴图（Texture Mapping）类型

• 漫反射贴图：模拟物体表面颜色，用于表现物体的基本颜色和材质。
• 光照贴图控制反光区域，用于增强物体表面的光泽感和反射效果。
• AO（环境光遮蔽）贴图：通过预计算好的贴图来模拟环境光遮蔽效果，使物体表面的阴影更加真实自然。
• 环境贴图（Environment Map）记录周围环境光线信息并将其应用于物体表面，以模拟物体反射周围环境的效果。
• 凹凸贴图（Bump Mapping）：根据定义的高度和临近的高度差计算切线，从而重新计算法线方向，
• 位移/视差贴图（Displacement / Parallax Mapping）：存储深度/高度，根据深度值计算位移或偏移，从而模拟出更加真实的凹凸效果。
• 法线贴图（Normal Mapping）：存储法线方向，根据视角计算计算更精确的效果

Bump Mapping：

如何求凹凸贴图法线方向：切线（根据高度差）逆时针旋转90度（根据旋转公式）

导数（Derivative）是微积分中的一个核心概念，描述了函数在某一点切线斜率，在这个凹凸贴图中，可以叫切线也可以叫导数

根据坐标差计算切线：已知曲线上的一个点P(x1​,y1​)，选择一个非常接近P的点Q(x2​,y2​)，其中x2​是x1​的一个微小增量，即x2​=x1​+Δx

两点式斜率公式（近似值）：斜率k（浮点值）=（y2​−y1​​ ）/ （x2​−x1​）

但上述是相对一个点计算2维的切线，但是纹理需要根据两个方向（UV）求出切线，

大体原理就是U方向的斜率作为x，V方向的斜率作为y，z设为常量1，对于的法线，分量xy旋转90度后的归一化结果

切线空间TBN：

以法线作为右手坐标系正z方向的局部空间，通过乘以m矩阵变换到世界空间，从而将纹理空间定义的贴图数据变换到世界空间，否则直接采样不正确的结果

……首先根据公式计算tangent，bitangent，normal
//然后变换到世界空间
vec3 T = normalize(vec3(model * vec4(tangent,   0.0)));
vec3 B = normalize(vec3(model * vec4(bitangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(normal,    0.0)));
mat3 TBN = mat3(T, B, N)
//再将采样的法线变换到世界空间
normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normalize(normal * 2.0 - 1.0);   
normal = normalize(fs_in.TBN * normal);

Displacement Mapping

和位移贴图不同，虽然都是模拟凹凸感，但并非根据高度差重新计算法线方向，而是根据高度计算新的纹理采样方向

总体来说视差贴图效果更好，但是需要模型足够精细

动态曲面细分：如何确定模型网格数量分界线，以在性能和效果做平衡

3维纹理：通常和3维噪声配合