FPGA视觉从入门到放弃——削苹果剩下的小波矩

与特征点等主流方法相比，小波矩是计算机视觉中古老的偏方，追溯到1962年。虽很少提及，但该方法的思路比较有意思。
后面以小波矩”从哪里来用到哪里去“为主线描述。数学渣顺便强行解释一波理论，请原谅我这里教材式的引用。~(￣▽￣)~(￣▽￣)~

1. 特征函数 1

(1) 引入

随机变量的特征函数完全定义了它的概率分布 2。

南大的傅渥成老爷对特征函数的引入有如下解释 3：
a. 实际应用中，计算各事件的概率分布函数困难，矩特征容易测量；
b. 计算矩时，分布函数要通过积分，而特征函数仅仅采用微分；各阶矩的形式更加统一；
c. 傅里叶空间与时域空间可以一一对应。

(2) 定义

假设概率空间中有随机变量 $X$，其对应的分布函数为$F(x)$。则$X$的特征函数为$e^{jtX}$的数学期望：

$$\begin{align} &\psi(t) =E(e^{jtX}) \\&=\int^{\infty}_{-\infty}e^{jtX}f(x)dx \\&or=E(cos(tX)+jsin(tX)) \\&=E(cos(tX))+jE(sin(tX)) \\&=\int^{\infty}_{-\infty}cos(tX)dF(x)+j\int^{\infty}_{-\infty}sin(tX)dF(x) \\&=\int^{\infty}_{-\infty}cos(tX)f(x)dx+j\int^{\infty}_{-\infty}sin(tX)f(x)dx \end{align}$$
其中 $f(x)$为X的概率密度函数。

$\psi(t)$是关于X的特征函数，但符号表达上的输入却为t。

(3) 性质

• $|\psi(t)|\le \psi(0)=1$
  由$|\psi(t)|=E(cos(tX)+jsin(tX))$知，$|\psi(\theta/X)|=|cos\theta+jsin\theta|<1$；

• $\psi(-t)=\overline {\psi(t)}$
  $|\psi(-t)|=E(cos(-tX)+jsin(-tX))=E(cos(tX)-jsin(tX))=\overline {\psi(t)}$；

• 假设X的特征函数为$\psi(t)$，那么$Y=aX+b$的特征函数为：
  

  $$\begin{align} \psi_{aX+b}(t)=E(e^{jt(aX+b)})=E(e^{jt(aX)})\cdot E(e^{jtb})=E(e^{j(at)X)})\cdot e^{jtb}=\psi(at)\cdot e^{jtb}； \end{align}$$

• $X$的特征函数半正定。

  波赫纳-辛钦定理： 若函数$\psi(t)(t \in R)$连续半正定，且$\psi(0)=1$，则$\psi(t)$一定为特征函数。

(4) 特征函数与矩

• 存在$X$的n阶矩，则$X$的特征函数的$k$阶导数$\psi^{(k)}(t)$存在，且
  $$E(X^{k})=j^{-k}\psi^{(k)}(0), k\le n$$
  上式表达了X的k阶矩与其特征函数的k阶导数之间的关系。

(5) 反演公式和唯一性定理

对于分布函数$F(x)$上的任意连续点$x_{1}$和$x_{2}(x_{1}<x_{2})$，有

$$F(x_{2})-F(x_{1})=\lim_{T\to \infty}\frac {1}{2\pi} \int^{T}_{-T}\frac{e^{-jtx_{1}}-e^{-jtx_{2}}}{jt}\psi(t)dt$$

上述公式说明了分布函数与特征函数间的关系，可以推出唯一性定理。

唯一性定理： 分布函数恒等的充分必要条件是对应的特征函数恒等。

如果特征函数绝对可积，则由分布函数与密度函数的关系可推出：

$$f(x)=\frac{\partial F(x)}{\partial x} =\frac{\partial \left(-\frac {1}{2\pi} \int^{\infty}_{-\infty}\frac{e^{-jtx} }{jt} \psi(t)dt\right)}{\partial x} =\frac {1}{2\pi} \int^{\infty}_{-\infty}e^{-jtx}\psi(t)dt$$

X为离散整数变量时同理。假设概率函数$F(X=k)=f_{k}，k=...-3,-2,-1,0,1,2,3...$，对应的特征函数为$\psi(t)=E(e^{jtk})=\sum^{\infty}_{k=-\infty}p_{k}e^{jtk}$，有：

$$f_{k}=\frac{1}{2\pi}\int^{\infty}_{-\infty}e^{-jtk}\psi(t)dt$$

直观上看，特征函数$|\psi(t)|\le 1$，所以$|f_{k}|\le\frac{1}{2\pi}\int^{\infty}_{-\infty}|e^{-jtk}|dt$，而$|e^{-jtk}|\le1$，有$|f_{k}|\le\frac{1}{2\pi}\int^{\infty}_{-\infty}dt$，这里把$\infty$改为$\pi$依然成立。所以有：

$$f_{k}=\frac{1}{2\pi}\int^{\pi}_{-\pi}e^{-jtk}\psi(t)dt$$

(6) 多维

一维随机变量的相关性质可以推广到多维。当多维随机变量$X_{i}, i=1,2,...,n$相互独立，则其特征函数为：

$$\psi(t_{1},...,t_{n})=\prod^{n}_{i=1}\psi(t_{i})$$

2. 基于矩的矩生成函数和特征函数 4

(1) 矩

2维随机变量$(x,y)$的密度函数$f(x,y)$的$(p+q)$阶矩$m_{pq}$的定义为：

$$m_{pq}=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}x^py^qf(x,y)dxdy， p,q=0,1,2,...$$

由唯一性定理知，不同的分段连续的的密度函数$f(x,y)$恒等的充分必要条件是它们的特征函数$m_{pq}$恒等。

(2) 矩生成函数

矩生成函数$M(u,v)$的定义为：

$$M(u,v)=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}e^{ux+vy}f(x,y)dxdy$$

由指数函数的泰勒展开式$e^{x}=1+x+\frac{x^2}{2!}+...+\frac{x^k}{k!}+...=\sum^{\infty}_{k=0}\frac{x^{k}}{k!}$得：

$$\begin{align} &M(u,v)=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}e^{ux}\cdot e^{vy}f(x,y)dxdy \\&=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\left(\sum^{\infty}_{p=0}\frac{(ux)^{p}}{p!}\right)\cdot \left(\sum^{\infty}_{q=0}\frac{(vy)^{q}}{q!}\right)f(x,y)dxdy \\&=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\left(\sum^{\infty}_{p=0}\frac{u^{p}}{p!} x^{p}\right)\left(\sum^{\infty}_{q=0}\frac{v^{q}}{q!} y^{q}\right)f(x,y)dxdy \\&=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\left(\sum^{\infty}_{p=0}\sum^{\infty}_{q=0}\frac{u^{p}}{p!}\frac{v^{q}}{q!}x^{p}y^{q}\right)f(x,y)dxdy \\&=\sum^{\infty}_{p=0}\sum^{\infty}_{q=0}\frac{u^{p}}{p!}\frac{v^{q}}{q!}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}x^{p}y^{q}f(x,y)dxdy \\&=\sum^{\infty}_{p=0}\sum^{\infty}_{q=0}\frac{u^{p}}{p!}\frac{v^{q}}{q!}m_{pq} \end{align}$$

(3) 特征函数

2维随机变量$(u,v)$的特征函数$\psi(u,v)$的定义类似于1维：

$$\begin{align} &\psi(u,v)=E(e^{jux+jvy}) \\&=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}e^{jux+jvy}f(x,y)dxdy \\&=\sum^{\infty}_{p=0}\sum^{\infty}_{q=0}\frac{(ju)^{p}}{p!}\frac{(jv)^{q}}{q!}m_{pq} \end{align}$$

(4) 中心矩

中心矩$\mu_{pq}$的定义如下：

$$\mu_{pq}=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}(x-\overline x)^{p}(y-\overline y)^{q}f(x,y)d(x-\overline x)d(y-\overline y)$$

假设随机变量$(x,y)$偏移至$(x+\alpha,y+\beta)$，则带入上式后，$\overline x$和$\overline y$变为$\overline x-\alpha$和$\overline y-\beta$。

中心矩的平移不变性：如果你已经接受“中心矩与随机变量的均值无关”这一观点。则可以理解“当均值发生变化时，中心矩的值依然不会变”。

Kuiming Hu提出的不变矩的几个几何矩不变量不再介绍，因为小波矩仅仅用到矩的特点。这里提及是因为他更加明确地描述了图像的特征函数和矩的关系。

3. 小波矩 6

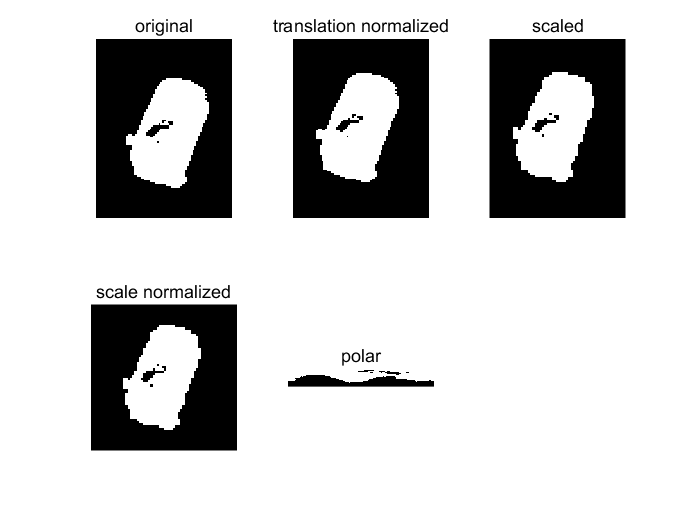
(1) 平移和尺度归一化

直接平移和缩放实现平移和尺度不变性。$f(x,y)$为笛卡尔平面坐标系中的坐标(x,y)的二值图像值(换句话说，$f(x,y)\in\{0,1\}$)。与极坐标系中的坐标$(r,\theta)$的关系如下：

$$\begin{align} &x=rcos(\theta) \\&y=rsin(\theta) \end{align}$$

计算目标形状的中心：

$$\begin{align} &x_{c}=\frac{m_{10}}{m_{00}} \\&y_{c}=\frac{m_{01}}{m_{00}} \end{align}$$

计算尺度因子：

$$s=\sqrt{\frac{m_{00}}{SIZE}}$$
其中， $m_{00}$为二值图像的“质量” 5， $SIZE$为图像的指定大小。 图像的大小从$m_{00}$到$SIZE$。

平移缩放后的坐标值为：

$$\binom{x_{ts}}{y_{ts}}=\binom{\frac{(x-x_{c})}{s}}{\frac{(y-y_{c})}{s}}$$

若目标区域无噪声，则图像的面积等于目标的面积$m_{00}$。
这就是个问题了~该方法有效的前提为目标物体的完整抠取。如果图像中有其它的噪声目标，矩计算对目标形状归一化失去意义。

(2) 旋转表达

极坐标系中的随机变量$(r,\theta)$的$(p+q)$阶矩为：

$$m_{pq}=\int^{\infty}_{0}\int^{2\pi}_{0}g_{p}(r)e^{jq\theta}f(r,\theta)rdrd\theta$$
其中， $g_{p}(r)$为 $r$的函数。

逆时针旋转$\beta$度的旋转矩为：

$$||m_{pq}e^{jq\beta}||=\sqrt{m_{pq}e^{jq\beta}\cdot \overline {m_{pq}}e^{-jq\beta}}=||m_{pq}||$$
旋转不变性得证。

旋转矩简化为：

$$m_{pq}=\int^{\infty}_{0}\left(\int^{2\pi}_{0}e^{jq\theta}f(r,\theta)d\theta \right)g_{p}(r)rdr=\int^{\infty}_{0}s_{q}(r)g_{p}(r)rdr$$
其中， $s_{q}(r)$为关于 $r$的1维变量($r$固定时代表相角域{ $0\le \theta\le 2\pi$}中极坐标点对应的二值像素值 $f(r,\theta)$的第q个频率的特征)。这里的 $r$覆盖整个平面，所以$m_{pq}$为全局特征；若 $r$范围有限，则旋转矩为局部特征。

• 当$g_{p}(r)=r^p$时，可获得Hu矩和Li矩；
  • 当$g_{p}(r)=\sum^{\frac{p-|q|}{2}}_{s=0}(-1)^s\cdot\frac{(p-s)!}{s!(\frac{p+|q|}{2}-s)!(\frac{p-|q|}{2}-s)!}$时，可获得Zernike矩；
  • 当$g_{p}(r)=\frac{4a^{n+1}}{\sqrt{2\pi(n+1)}}\sigma_{w}cos(2\pi f_{0}(2r-1))exp\left(-\frac{(2r-1)^2}{2\sigma_{w}^2(n+1)}\right)$时，可获得基于近似3阶B样条小波的矩。

  • B样条小波逐点渐进收敛为Gabor函数。3阶B样条小波的近似误差小于3% 5。

    (3) 小波矩特征

    沈分析Hu矩，Li矩和Zernike矩在全局图像空间中计算。假设2个相似物体矩的模长以及噪声分别为$||m_{pq}||$，$||m_{pq}'||$和$\delta_{pq}$，有：
    

    $$||m_{pq}||=||m_{pq}'||+\Delta_{pq}+\delta_{pq}$$
    全局空间中 $\Delta_{pq}<\delta_{pq}$，即 图像噪声淹没了物体的相似性特征。而小波矩适合提取局部可分特征。
    视 $g_{p}(r)$为小波基函数，且函数族为：
    $$\psi^{(c,d)}(x)=\frac{1}{\sqrt{c}}g_{p}\left(\frac{x-d}{c}\right)$$
    其中， $c$为膨胀参数，$d$为偏移参数。

    图像大小始终在径向域{$r\le 1$}中，构造$r=\frac{x-d}{c}=\frac{x-0.5n*0.5^m}{0.5^m}=\frac{x}{0.5^m}-0.5n$，所以有：
    

    $$\psi^{(c,d)}(x)=2^{\frac{m}{2}}g_{p}\left(2^mx-0.5n\right)$$
    由于 $r=2^mx-0.5n\le 2^mx-0.5*2^{m+1}=2^m(x-1)$，令 $r\le1$，得 $x\le \frac{1}{2^m}+1$。所以如果要采样 $r\le 1$的完整区域，存在一部分 $x\in(1,\frac{1}{2^m}+1]$造成过采样。

    与图像恢复相比，目标分类并不需要物体的完整小波特征。特征选择后去掉冗余和敏感的噪声。

    以B样条小波函数为基函数的小波函数族的特征在分类时定义为其L2-模。因此得到完备的小波矩特征：
    

    $$||m_{mnq}||=||\int^{1}_{0}\left(\int^{2\pi}_{0}e^{jq\theta}f(r,\theta)d\theta \right)\cdot 2^{\frac{m}{2}}g_{p}\left(\sum^{3}_{m=0}\sum^{2^{(m+1)}}_{n=0}(2^mx-0.5n)\right)rdr||$$
    径向域{ $0\le r \le 1$}上的积分表达了 $f(r,\theta)$在不同尺度上的特征。

    (4) 小波矩特征提取

    假设目标的二值图像为完整苹果皮摊开的2维平面。削苹果时，刀与苹果皮的当前接触点的二值特征记为$f(r,\theta)$，$r$为刀离苹果垂直轴的半径，$\theta$为刀离刚下刀削时水平方向的角度，$\psi^{(c,d)}(x)$可以理解为根据环境光照等对接触点特征的影响因子，削出来的苹果皮拉平作为完整的1维小波矩特征。所以，小波矩是削苹果后留下的条状苹果皮。

    3. 结果

    该方法仅要求无噪声的二值图像，所以暂时先采用预处理后的二值图像数据集。

    (1) 获取极坐标图像

    玩具汽车的归一化图像和极化图像。
    

    (2) 小波函数族

    

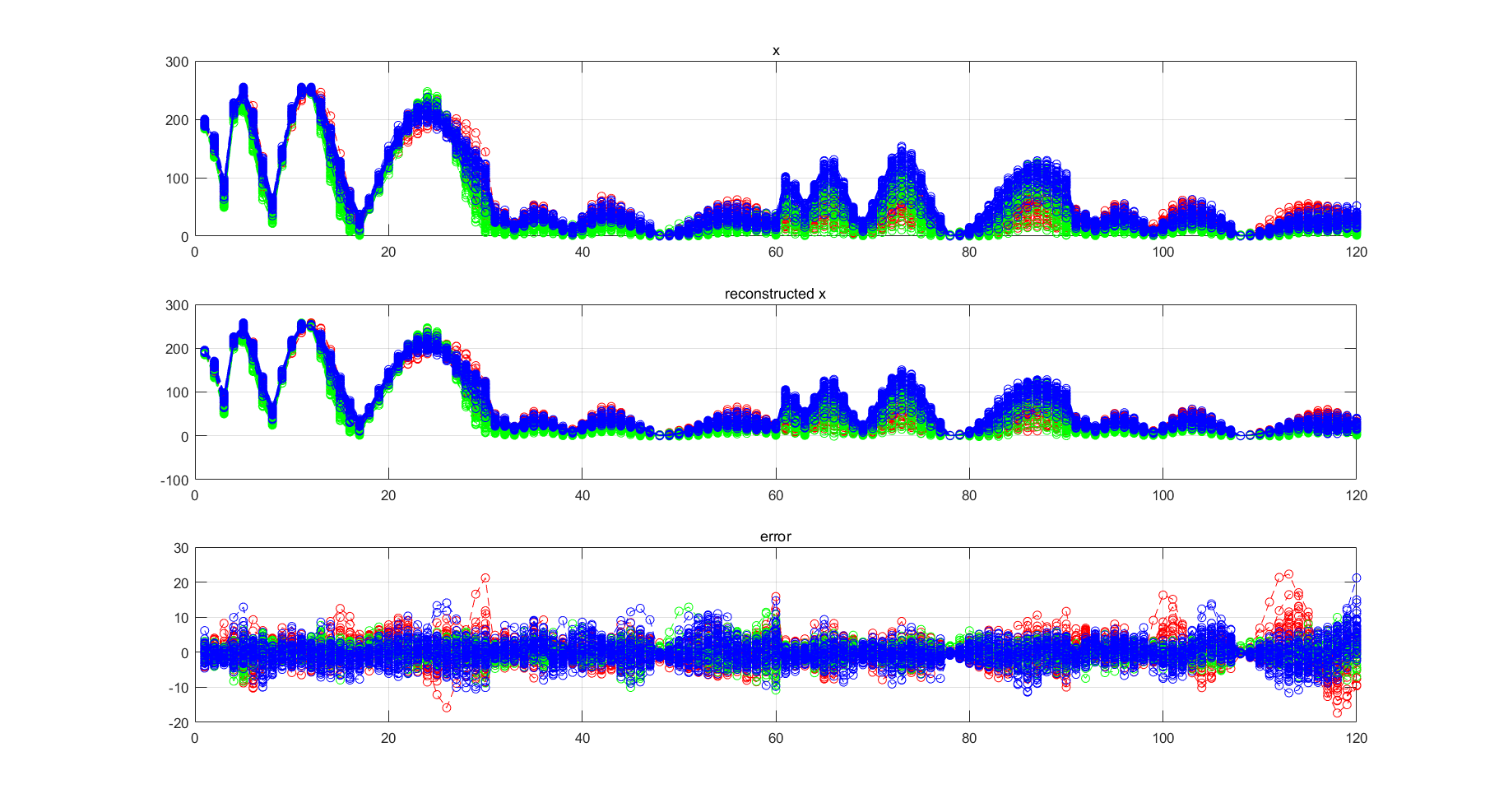
    (3) 完整的小波矩特征

    红，绿和蓝色分别为3类玩具的小波矩特征。
    

    4. 总结

    (1) 优点

    二值图像中每个像素点的坐标可以看作图像笛卡尔空间(或极坐标)空间中的2维随机变量。假设二值随机变量的概率定义为该随机变量值为真的概率，那么2维随机变量就有了自己的概率分布。由于特征函数能够更有效地表示概率分布，同时特征函数与矩之间有着明确的关系，所以矩特征可以替换二值图像概率分布的定义。
    基于小波特征的矩与其它矩特征相比，在全局特征的噪声淹没目标特征的情况下，更加适合局部特征的提取。

    (2) 局限

    小波矩的基函数固定。即使表现出色，和更贴近目标样本的稀疏编码等方法相比，手动确定基函数直观感觉该方法还是对样本更为冷淡一些。
    整个方法的基础是像素点为目标点的概率分布，复杂场景中抽取二值前景图像本身就是个open problem，所以应用场合挺有限。

    ---

    注：参考的资源和文献的链接位于引用时内容的右侧。