1、Cost Function
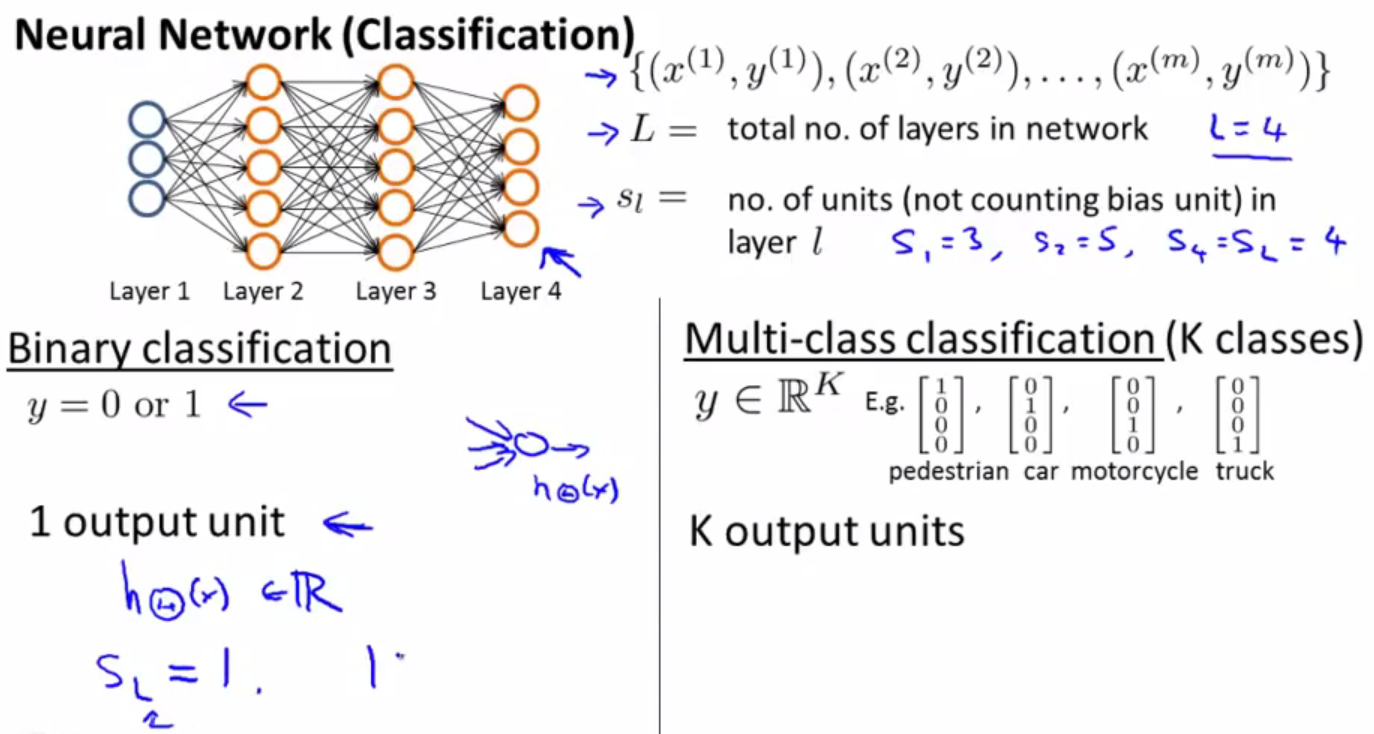
主要考虑的是分类问题(K classesde 的多类分类问题),下图中给出了一些标记的含义:
在逻辑回归中我们的代价函数如下:
在神经网络中,我们有多个输出变量,所以h函数是一个维度为K的向量,代价函数如下:
这两个代价函数的思想是一样的,我们通过代价函数来计算预测结果与真实情况的误差。不同的是在神经网络中我们对于每一行特征都会给出K个预测,我们要从这K个预测中选择可能性最大的作为预测结果,再与实际结果比较。神经网络中的归一项只是排除了每一层的theta0后的矩阵和。
2、反向传播算法
前面我们已经讲过前向传播算法,即根据初始的参数值,从第一层开始正向一层一层的进行计算,直到最后一层h(x),即神经网络的预测结果。现在我们要让神经网络进行学习,也就是要最小化代价函数,我们需要计算代价函数的偏导数,所以下面采用后向传播算法:首先用前向传播算法计算出预测值从而获得最后一层的误差,然后再一层一层的反向求出各层的误差直到第一层,从而调整和优化权重值。
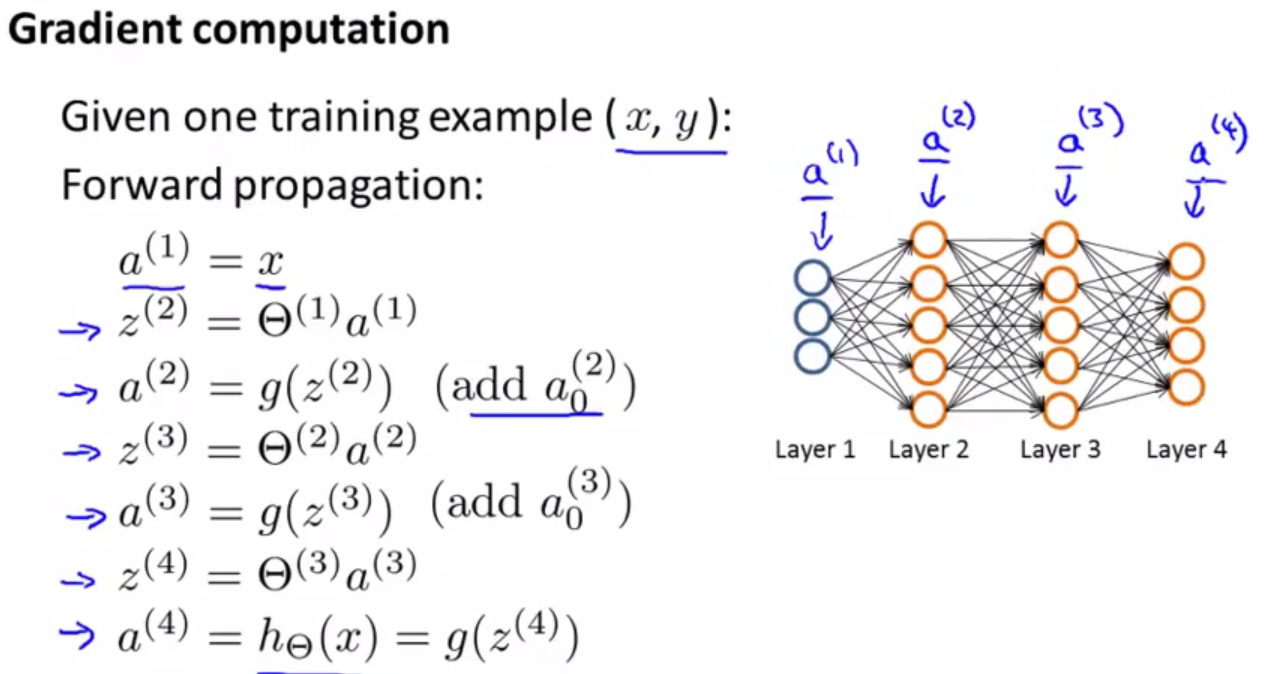
下面还是先用一个例子来说明:
首先用前向传播的方法算出各层的结果
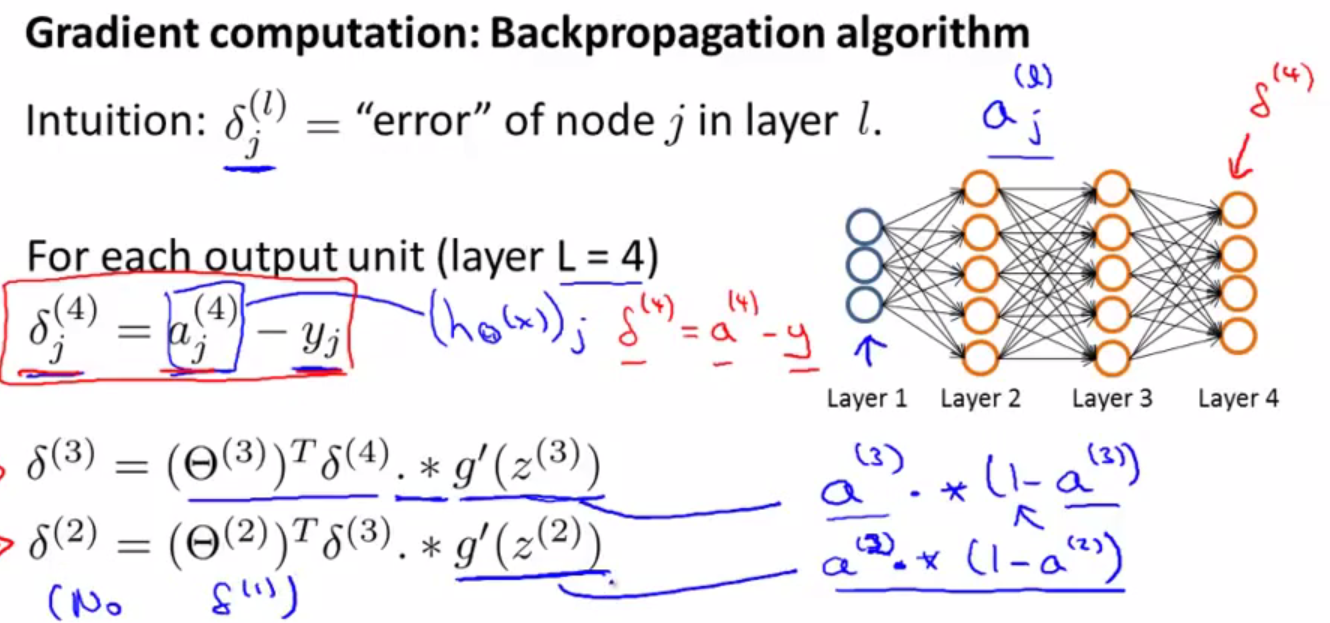
然后用后向传播的方法反向得到各层误差:我们并不计算第一层的误差,因为第一层为输入层,我们认为它没有误差。
这部分的证明过程在下面这个博客里有详细的解释,非常感谢博主的讲解.
http://blog.csdn.net/jingshui1216/article/details/9285543
然后我们得到下面的伪代码:
感觉这部分我还没有理解透彻,所以先不乱写了,回头再看看数学证明和Mitchell教授的《机器学习》的第四章“人工神经网络”再来补充自己的理解。
3、将矩阵展开为向量
使用Theta(:)可以将矩阵的所以元素取出然后置成向量;最后可以用reshape来还原,下图为例子:
学习过程的实现:
4、梯度检验(Gradient Checking)
当我们对一个较复杂的模型使用梯度下降时,可能会存在一些不易察觉的错误:虽然代价函数看上去在不断减小,但是结果却存在很大误差。
为了避免这样的错误,我们采取一种叫做梯度的数值校验方法。这种方法的思想是通过估计梯度值来教研我们计算的导数值是否正确。
对梯度的估计方法:在代价函数上沿着切线的方向选择两个非常近的点,然后近似计算梯度值。即对于给定的Theta,我们计算它两边非常近的两个点的代价函数值,这两个代价值得平均就是Theta处的近似梯度。
如果Theta是一个向量的话,我们则需要对偏导数进行校验:
最后我们还需要与计算出的偏导数进行对比校验;
对于神经网络而言,我们将通过反向传播方法计算出的偏导数存储在矩阵D中,校验时,我们将该矩阵展开为DVector,同时也将Theta矩阵展开为向量,针对每一个theta都计算一个近似的梯度值存储在近似梯度矩阵中,最后将其与D进行比较:
注:我们需要在使用反向传播算法计算出矩阵D后进行数值梯度校验,校验正确后就需要关闭梯度校验,然后再进行学习。
(因为如果每一步学习前都进行梯度校验,算法实现将会非常慢!)
5、随机初始化
任何优化算法都需要设置一些初始参数,回忆逻辑回归的octave实现时,我们使用的代码是theta = zeros(n+1,1);即全部初始为0,这在逻辑回归中是可行的,但是对于神经网络是不可行的。因为如果初始的参数都为0,那么后续层内各个激活单元的值将相同。(将所有参数设为一样的非0 值也会导致同样的结果)
所以我们通常将初始参数设置为正负epsilon之间的随机值,实现方式:
6、小结
总结一下使用神经网络时的步骤:
1、选择网络结构,即决定选择多少层以及各层的单元数
第一层即输入层:决定多少特征量
最后一层输出层:需要多少训练结果的类
隐藏层:如果隐藏层的层数大于1,确保每个隐藏层的单元数相同(通常隐藏层单元的个数越多越好)
2、训练神经网络:
1、随机初始化参数(注意不能theta值不能都相同)
2、利用正向传播算法计算所有的h(x)
3、编写计算代价函数J的代码
4、利用反向传播算法计算所有的偏导数
5、利用数值校验方法校验4中的偏导数(如果正确,关闭校验,往下执行)
6、利用优化算法来最小化代价函数









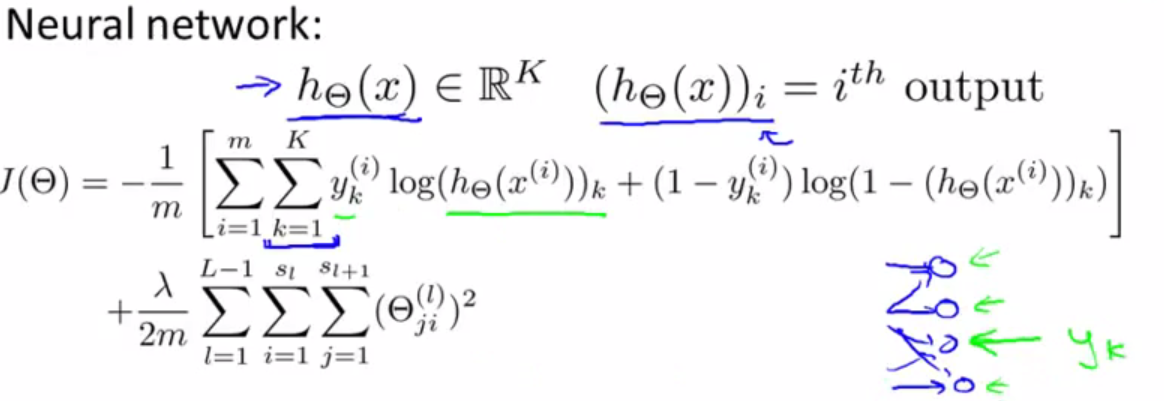























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








