DPO中的长度剥削问题与创新性正则化解决方案

DPO中的长度剥削问题与创新性正则化解决方案

引言

在大型语言模型（LLM）的训练中，强化学习人类反馈（RLHF）一直是提升模型指令遵循能力的关键技术。然而，RLHF的一个已知问题是模型容易利用人类偏见，例如偏好冗长的回答。这种“长度剥削”（length exploitation）现象导致模型生成过长的回答，而不一定提升实际质量。直接偏好优化（DPO）作为一种高效的替代RLHF的直接对齐算法，因其无需显式奖励模型和强化学习阶段而广受欢迎。然而，DPO中的长度剥削问题尚未被充分研究。本文介绍了一篇由斯坦福大学研究团队撰写的论文（Park et al., 2024），首次系统性地分析了DPO中的长度剥削问题，并提出了一种简单而有效的正则化方法来解决这一问题。

paper: https://arxiv.org/pdf/2403.19159

问题描述

DPO中的长度剥削

论文首次揭示了DPO训练中的长度剥削现象，即模型倾向于生成远超数据集分布的冗长回答。例如，在Anthropic的Helpful and Harmless（HH）对话数据集和Reddit TL;DR摘要数据集上，DPO生成的回答平均长度显著高于偏好和非偏好回答的长度分布（如图2所示）。这种现象与传统RLHF中的冗长问题类似，但由于DPO没有显式奖励模型，问题表现形式更为复杂。

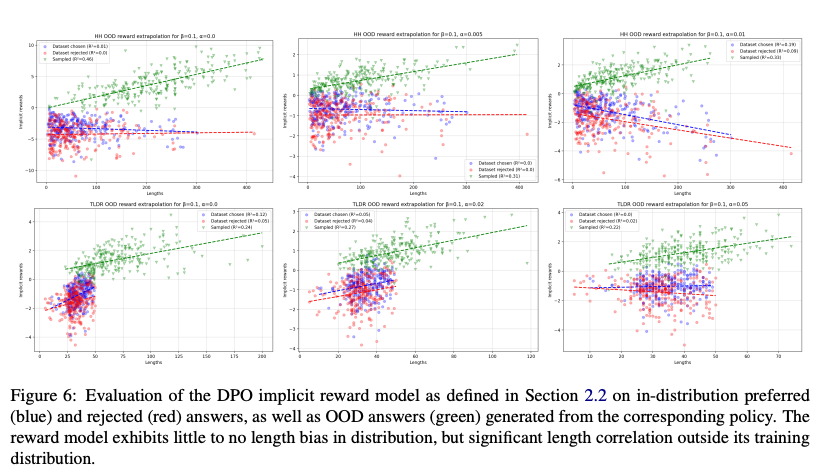
研究发现，DPO的长度剥削与分布外（out-of-distribution, OOD）引导（bootstrapping）密切相关。尽管DPO仅使用离线反馈数据训练，其隐式奖励函数（由公式5定义）在分布内对长度几乎无偏见，但在分布外（即模型生成的回答）表现出显著的长度偏见，长度解释了奖励方差的30-46%（图6）。这表明DPO在优化过程中无意中放大了反馈数据中的微小长度偏见。

长度剥削的影响

长度剥削不仅导致生成回答冗长，还影响模型的实际性能。在Alpaca Eval基准测试中，开源模型在整体性能上可与闭源模型媲美，但在长度校正后的性能上显著落后（图1）。此外，论文指出，DPO的早期收敛现象（通常在几百个梯度步内达到最佳性能）可能也与长度剥削有关。模型迅速学会利用长度偏见以提高奖励，但未能捕捉更复杂的偏好特征（图5）。

创新点

论文提出了以下创新点，为DPO中的长度剥削问题提供了理论和实证解决方案：

1. 理论推导：长度正则化的DPO目标

为了控制DPO中的长度剥削，作者在RL目标（公式3）中引入了一个长度惩罚项α|y|，从而推导出正则化的DPO目标（公式9）：

$${\mathcal{L}}_{\mathrm{R}-\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{\mathrm{ref}}\right)=-{\mathbb{E}}_{\left(\mathbf{x},{\mathbf{y}}_w,{\mathbf{y}}_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }\left({\mathbf{y}}_w\mid \mathbf{x}\right)}{{\pi }_{\mathrm{ref}}\left({\mathbf{y}}_w\mid \mathbf{x}\right)}-\beta \log \frac{{\pi }_{\theta }\left({\mathbf{y}}_l\mid \mathbf{x}\right)}{{\pi }_{\mathrm{ref}}\left({\mathbf{y}}_l\mid \mathbf{x}\right)}+\left(\alpha \left|{\mathbf{y}}_w\right|-\alpha \left|{\mathbf{y}}_l\right|\right)\right)\right]$$

这一目标通过在分类损失的logit中添加正则化项($\left(\alpha \left|{\mathbf{y}}_w\right|-\alpha \left|{\mathbf{y}}_l\right|\right)$)，动态调整学习率：当偏好回答较短时上调梯度权重，当较长时下调权重。这种方法在理论上等价于在隐式奖励函数中加入长度惩罚，从而有效控制模型生成回答的长度。

2. 实证验证：显著的长度控制与性能提升

作者在HH和TL;DR数据集上使用Pythia 2.8B模型进行了广泛实验，验证了正则化方法的有效性。实验结果表明：

• 长度控制：正则化DPO（R-DPO）生成的回答长度更接近于初始监督微调（SFT）模型，且显著减少了分布外长度的生成（图2）。
• 性能提升：在GPT-4作为评判者（尽管其存在长度偏见）的情况下，R-DPO在HH和TL;DR任务上分别实现了高达20%和15%的长度校正胜率提升（图3）。
• 训练稳定性：与标准DPO相比，R-DPO在训练过程中表现出更稳定的胜率提升，避免了因长度剥削导致的早期收敛（图5）。

此外，在Microsoft Phi-2模型和Ultrafeedback数据集上的补充实验进一步确认了正则化方法在减少长度同时略微提升下游性能（表2）。

3. OOD引导的解释

论文深入分析了长度剥削的根源，发现DPO的隐式奖励函数在分布外表现出显著的长度偏见。这种现象类似于传统RLHF中的奖励过优化，但其机制在DPO中更为隐晦。通过比较分布内和分布外的奖励行为（图6-8），作者明确了长度剥削是由模型在优化过程中对微小偏见的放大引起的。这一发现为理解DPO的优化动态提供了新视角。

意义与局限性

意义

这项工作首次将长度剥削问题的研究扩展到DPO，填补了直接对齐算法在偏见控制方面的研究空白。其提出的正则化方法简单且高效，适用于现有的DPO训练流程，且无需额外的计算开销。实验结果表明，该方法不仅能有效控制冗长问题，还能提升模型的长度校正性能。这对开源社区尤为重要，因为许多顶级开源模型（如HuggingFace Open LLM Leaderboard上的9/10模型）都使用了DPO训练。

局限性

论文也指出了方法的局限性：

• 正则化方法针对长度惩罚，可能无法解决其他维度的剥削问题。
• 实验主要基于中小规模模型（Pythia 2.8B, Phi-2）和公开数据集，长度剥削的规模律（scaling laws）以及在更大模型和数据上的表现尚待探索。
• 方法仅针对DPO，其他直接对齐算法的行为可能有所不同。

结论

这篇论文为DPO中的长度剥削问题提供了深刻的理论洞见和实用的解决方案。其正则化方法通过在优化目标中引入长度惩罚，有效控制了模型的冗长倾向，同时提升了长度校正后的性能。对于深度学习研究者而言，这项工作不仅揭示了DPO优化中的潜在陷阱，还为改进直接对齐算法提供了新思路。未来，研究者可以进一步探索正则化方法在其他对齐算法中的适用性，以及长度剥削在不同模型规模和数据质量下的表现。

为了推导正则化的DPO目标（公式9），我们需要从引入长度惩罚项的强化学习（RL）目标（公式3）开始，逐步推导到最终的正则化DPO损失函数。以下是详细的推导过程，基于论文中的方法和数学框架。

DPO长度正则化目标的推导过程

1. 原始RL目标与长度惩罚项

在标准的强化学习从人类反馈（RLHF）目标中，优化策略(${\pi }_{\theta }$)的目标是最大化期望奖励，同时通过KL散度正则化防止策略偏离参考策略(${\pi }_{\text{ref}}$)。原始RL目标（公式3）为：

$$\underset{{\pi }_{\theta }}{\max }{\mathbb{E}}_{\mathbf{x}\sim \mathcal{D},\mathbf{y}\sim {\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})}\left[r_{\varphi }(\mathbf{x},\mathbf{y})\right]-\beta {\mathbb{D}}_{\mathrm{KL}}\left[{\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})\Vert {\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})\right]$$

其中：

• ($r_{\varphi }(\mathbf{x},\mathbf{y})$) 是奖励模型，表征人类偏好。
• ($\beta$) 是控制KL散度惩罚强度的超参数。
• (${\mathbb{D}}_{\mathrm{KL}}$) 是KL散度，确保策略(${\pi }_{\theta }$)不会偏离(${\pi }_{\text{ref}}$)太远。

为了控制长度剥削，作者在奖励函数中引入一个长度惩罚项($\alpha |\mathbf{y}|$)，其中($\alpha$)是超参数，($|\mathbf{y}|$)表示回答($\mathbf{y}$)的token长度。因此，修改后的RL目标（公式6）为：

$$\underset{{\pi }_{\theta }}{\max }{\mathbb{E}}_{\mathbf{x}\sim \mathcal{D},\mathbf{y}\sim {\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})}\left[r(\mathbf{x},\mathbf{y})-\alpha |\mathbf{y}|\right]-\beta {\mathbb{D}}_{\mathrm{KL}}\left[{\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})\Vert {\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})\right]$$

这里，奖励函数变为($r(\mathbf{x},\mathbf{y})-\alpha |\mathbf{y}|$)，表示在原始奖励基础上减去长度惩罚。

2. 推导最优策略

为了推导正则化的DPO目标，我们需要找到上述修改后RL目标的最优策略(${\pi }^{\ast }$)。根据DPO的理论框架（Rafailov et al., 2023），我们可以利用约束优化问题的最优解形式。对于带有KL散度的RL目标，最优策略可以表示为：

$${\pi }^{\ast }(\mathbf{y}\mid \mathbf{x})=\frac{1}{Z(\mathbf{x})}{\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})e^{\frac{1}{\beta }\left[r(\mathbf{x},\mathbf{y})-\alpha |\mathbf{y}|\right]}$$

其中：

• ($Z(\mathbf{x})={\sum }_{\mathbf{y}}{\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})e^{\frac{1}{\beta }\left[r(\mathbf{x},\mathbf{y})-\alpha |\mathbf{y}|\right]}$) 是归一化常数（配分函数），确保(${\pi }^{\ast }(\mathbf{y}\mid \mathbf{x})$)是一个有效的概率分布。
• 指数项中的($\frac{1}{\beta }$)来源于KL散度惩罚的强度。

这一形式可以通过拉格朗日乘子法推导，具体来说，优化目标等价于最小化以下拉格朗日函数：

$$\mathcal{L}(\pi )=-{\mathbb{E}}_{\mathbf{y}\sim \pi (\mathbf{y}\mid \mathbf{x})}\left[r(\mathbf{x},\mathbf{y})-\alpha |\mathbf{y}|\right]+\beta {\mathbb{D}}_{\mathrm{KL}}\left[\pi (\mathbf{y}\mid \mathbf{x})\Vert {\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})\right]$$

对($\pi (\mathbf{y}\mid \mathbf{x})$)求变分导数并令其为零，可以得到上述最优策略形式（详细推导见Rafailov et al., 2023）。

3. 奖励函数的重新参数化

接下来，我们需要将奖励函数($r(\mathbf{x},\mathbf{y})$)表示为最优策略(${\pi }^{\ast }$)和参考策略(${\pi }_{\text{ref}}$)的函数。对最优策略公式取对数并整理：

$$\log {\pi }^{\ast }(\mathbf{y}\mid \mathbf{x})=\log {\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})+\frac{1}{\beta }\left[r(\mathbf{x},\mathbf{y})-\alpha |\mathbf{y}|\right]-\log Z(\mathbf{x})$$

移项得到：

$$r(\mathbf{x},\mathbf{y})-\alpha |\mathbf{y}|=\beta \log \frac{{\pi }^{\ast }(\mathbf{y}\mid \mathbf{x})}{{\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})}+\beta \log Z(\mathbf{x})$$

因此，奖励函数可以表示为：

$$r(\mathbf{x},\mathbf{y})=\beta \log \frac{{\pi }^{\ast }(\mathbf{y}\mid \mathbf{x})}{{\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})}+\beta \log Z(\mathbf{x})+\alpha |\mathbf{y}|$$

这与论文中的公式8一致：

$$r(\mathbf{x},\mathbf{y})=\beta \log \frac{{\pi }^{\ast }(\mathbf{y}\mid \mathbf{x})}{{\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})}+\beta \log Z(\mathbf{x})+\alpha |\mathbf{y}|$$

此表达式表明，奖励函数可以通过最优策略和长度惩罚重新参数化，($\beta \log Z(\mathbf{x})$)是一个与($\mathbf{y}$)无关的常数项。

4. 代入奖励建模目标

在标准DPO中，奖励建模阶段使用Bradley-Terry模型来拟合人类偏好分布：

$$p\left({\mathbf{y}}_w\succ {\mathbf{y}}_l\mid \mathbf{x}\right)=\frac{\exp \left(r(\mathbf{x},{\mathbf{y}}_w)\right)}{\exp \left(r(\mathbf{x},{\mathbf{y}}_w)\right)+\exp \left(r(\mathbf{x},{\mathbf{y}}_l)\right)}=\sigma \left(r(\mathbf{x},{\mathbf{y}}_w)-r(\mathbf{x},{\mathbf{y}}_l)\right)$$

其中($\sigma$)是logistic函数。奖励建模的损失函数（公式2）为：

$${\mathcal{L}}_R(r_{\varphi },\mathcal{D})=-{\mathbb{E}}_{\left(\mathbf{x},{\mathbf{y}}_w,{\mathbf{y}}_l\right)\sim \mathcal{D}}\left[\log \sigma \left(r_{\varphi }(\mathbf{x},{\mathbf{y}}_w)-r_{\varphi }(\mathbf{x},{\mathbf{y}}_l)\right)\right]$$

将重新参数化的奖励函数（公式8）代入，计算偏好对的奖励差：

$$r(\mathbf{x},{\mathbf{y}}_w)=\beta \log \frac{{\pi }^{\ast }({\mathbf{y}}_w\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_w\mid \mathbf{x})}+\beta \log Z(\mathbf{x})+\alpha |{\mathbf{y}}_w|$$

$$r(\mathbf{x},{\mathbf{y}}_l)=\beta \log \frac{{\pi }^{\ast }({\mathbf{y}}_l\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_l\mid \mathbf{x})}+\beta \log Z(\mathbf{x})+\alpha |{\mathbf{y}}_l|$$

相减得到：

$$r(\mathbf{x},{\mathbf{y}}_w)-r(\mathbf{x},{\mathbf{y}}_l)=\beta \log \frac{{\pi }^{\ast }({\mathbf{y}}_w\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_w\mid \mathbf{x})}-\beta \log \frac{{\pi }^{\ast }({\mathbf{y}}_l\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_l\mid \mathbf{x})}+\alpha |{\mathbf{y}}_w|-\alpha |{\mathbf{y}}_l|$$

注意到($\beta \log Z(\mathbf{x})$)在差值中被抵消。将此差值代入奖励建模损失中的logistic函数：

$$r(\mathbf{x},{\mathbf{y}}_w)-r(\mathbf{x},{\mathbf{y}}_l)=\beta \left(\log \frac{{\pi }^{\ast }({\mathbf{y}}_w\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_w\mid \mathbf{x})}-\log \frac{{\pi }^{\ast }({\mathbf{y}}_l\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_l\mid \mathbf{x})}\right)+\alpha (|{\mathbf{y}}_w|-|{\mathbf{y}}_l|)$$

5. 正则化DPO损失函数

在DPO中，策略(${\pi }_{\theta }$)直接优化偏好数据，假设(${\pi }_{\theta }\approx {\pi }^{\ast }$)。因此，将(${\pi }^{\ast }$)替换为(${\pi }_{\theta }$)，代入奖励差值，得到正则化的DPO损失函数：

$${\mathcal{L}}_{\mathrm{R}-\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{\mathrm{ref}}\right)=-{\mathbb{E}}_{\left(\mathbf{x},{\mathbf{y}}_w,{\mathbf{y}}_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \left(\log \frac{{\pi }_{\theta }({\mathbf{y}}_w\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_w\mid \mathbf{x})}-\log \frac{{\pi }_{\theta }({\mathbf{y}}_l\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_l\mid \mathbf{x})}\right)+\alpha (|{\mathbf{y}}_w|-|{\mathbf{y}}_l|)\right)\right]$$

整理表达式：

$${\mathcal{L}}_{\mathrm{R}-\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{\mathrm{ref}}\right)=-{\mathbb{E}}_{\left(\mathbf{x},{\mathbf{y}}_w,{\mathbf{y}}_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }({\mathbf{y}}_w\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_w\mid \mathbf{x})}-\beta \log \frac{{\pi }_{\theta }({\mathbf{y}}_l\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_l\mid \mathbf{x})}+\alpha |{\mathbf{y}}_w|-\alpha |{\mathbf{y}}_l|\right)\right]$$

这正是论文中的公式9：

$${\mathcal{L}}_{\mathrm{R}-\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{\mathrm{ref}}\right)=-{\mathbb{E}}_{\left(\mathbf{x},{\mathbf{y}}_w,{\mathbf{y}}_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }({\mathbf{y}}_w\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_w\mid \mathbf{x})}-\beta \log \frac{{\pi }_{\theta }({\mathbf{y}}_l\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_l\mid \mathbf{x})}+\left(\alpha |{\mathbf{y}}_w|-\alpha |{\mathbf{y}}_l|\right)\right)\right]$$

6. 解释正则化项的作用

正则化项($\alpha (|{\mathbf{y}}_w|-|{\mathbf{y}}_l|$))在损失函数的logit中起到动态调整学习率的作用：

• 当偏好回答(${\mathbf{y}}_w$)比非偏好回答(${\mathbf{y}}_l$)短（即($|{\mathbf{y}}_w|<|{\mathbf{y}}_l|$)），正则化项为负，增加logit值，相当于上调梯度权重，促进学习短回答。
• 当(${\mathbf{y}}_w$)比(${\mathbf{y}}_l$)长（即($|{\mathbf{y}}_w|>|{\mathbf{y}}_l|$)），正则化项为正，减小logit值，相当于下调梯度权重，抑制冗长回答。

这种机制有效地在优化过程中引入长度约束，防止模型过度偏向生成长回答。

结论

通过在RL目标中引入长度惩罚项($\alpha |\mathbf{y}|$)，并利用DPO的理论框架，我们推导出了正则化的DPO损失函数（公式9）。这一推导过程从修改RL目标开始，通过最优策略的解析形式和奖励函数的重新参数化，最终将长度惩罚融入DPO的分类损失中。所得的正则化目标在理论上等价于在隐式奖励函数中加入长度惩罚，能够有效控制DPO中的长度剥削问题。

这部分内容是论文的核心发现之一，揭示了直接偏好优化（DPO）中长度剥削（length exploitation）问题的根本原因，即分布外（out-of-distribution, OOD）引导（bootstrapping）导致的隐式奖励函数的长度偏见。以下是对这一现象的详细解释，涵盖其背景、机制、实验证据以及意义，面向熟悉RLHF和DPO的深度学习研究者。

DPO中长度剥削与分布外引导的详细解释

1. 背景：DPO与隐式奖励函数

直接偏好优化（DPO）是一种替代传统强化学习从人类反馈（RLHF）的直接对齐算法。传统RLHF通过三个阶段优化语言模型：监督微调（SFT）、奖励建模和强化学习优化。DPO的创新在于通过直接优化偏好数据，绕过了显式奖励模型和强化学习阶段。DPO假设奖励函数可以通过策略(${\pi }_{\theta }$)和参考策略(${\pi }_{\text{ref}}$)之间的对数概率比来隐式表示，定义为（公式5）：

$$r_{\theta }(\mathbf{x},\mathbf{y})=\beta \log \frac{{\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})}{{\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})}$$

其中：

• (${\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})$) 是当前策略，(${\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})$) 是参考策略（通常为SFT模型）。
• ($\beta$) 是控制KL散度惩罚强度的超参数。
• ($r_{\theta }(\mathbf{x},\mathbf{y})$) 是隐式奖励函数，表征模型对回答($\mathbf{y}$)给定输入($\mathbf{x}$)的偏好程度。

DPO通过优化以下损失函数（公式4）直接训练策略(${\pi }_{\theta }$)：

$${\mathcal{L}}_{\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{\text{ref}}\right)=-{\mathbb{E}}_{\left(\mathbf{x},{\mathbf{y}}_w,{\mathbf{y}}_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }({\mathbf{y}}_w\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_w\mid \mathbf{x})}-\beta \log \frac{{\pi }_{\theta }({\mathbf{y}}_l\mid \mathbf{x})}{{\pi }_{\text{ref}}({\mathbf{y}}_l\mid \mathbf{x})}\right)\right]$$

其中(${\mathbf{y}}_w$)和(${\mathbf{y}}_l$)分别是偏好和非偏好回答，($\sigma$)是logistic函数。由于DPO仅依赖离线偏好数据集($\mathcal{D}$)，且不涉及在线采样或显式奖励模型，传统RLHF中的奖励过优化（reward overoptimization）问题在DPO中的表现形式尚不清楚。

2. 长度剥削现象

论文发现，DPO训练的模型倾向于生成远超偏好数据集长度分布的冗长回答。例如，在Anthropic的Helpful and Harmless（HH）和Reddit TL;DR数据集上，DPO生成的回答平均长度是偏好和非偏好回答的两倍，且显著偏离数据集的长度分布（图2）。这种现象被称为“长度剥削”，类似于传统RLHF中的冗长问题，但其机制在DPO中更复杂，因为DPO没有显式奖励模型。

关键问题是：为什么仅使用离线数据的DPO会放大长度偏见？论文指出，这与隐式奖励函数在分布外（OOD）的行为密切相关，具体表现为“分布外引导”（OOD bootstrapping）。

3. OOD引导的机制

3.1 隐式奖励函数的分布内行为

在DPO中，隐式奖励函数($r_{\theta }(\mathbf{x},\mathbf{y})$)是在离线偏好数据集($\mathcal{D}$)上训练得到的。数据集($\mathcal{D}$)包含三元组(($\mathbf{x},{\mathbf{y}}_w,{\mathbf{y}}_l)$)，其中(${\mathbf{y}}_w$)是偏好回答，(${\mathbf{y}}_l$)是非偏好回答。论文通过实验分析了($r_{\theta }$)在分布内（即数据集中的(${\mathbf{y}}_w$)和(${\mathbf{y}}_l$)）的行为，发现：

• 弱长度相关性：在分布内，($r_{\theta }$)对回答长度的偏见非常弱，甚至在某些情况下呈负相关（图6）。这表明，训练数据中的长度偏见（偏好回答略长于非偏好回答，见表1）并未直接导致隐式奖励函数对长度的强偏好。
• 数据分布的限制：由于DPO仅使用离线数据，(${\pi }_{\theta }$)和($r_{\theta }$)的优化受到数据集($\mathcal{D}$)的长度分布约束。在HH和TL;DR数据集中，偏好回答的平均长度仅比非偏好回答略长（例如，HH中为79.6 vs. 75.7 tokens，TL;DR中为37.9 vs. 35.2 tokens），因此分布内的奖励函数难以学习到强烈的长度偏见。

3.2 分布外的长度偏见

尽管分布内奖励函数对长度偏见较弱，但在分布外（即(${\pi }_{\theta }$)生成的回答），情况完全不同。论文通过以下实验揭示了这一现象：

• 实验设置：作者训练了DPO模型（使用不同($\beta$)和正则化参数($\alpha$)），并评估隐式奖励函数($r_{\theta }$)在两种数据上的表现：
  • 分布内数据：来自训练数据集的偏好和非偏好回答（图6中的蓝色和红色点）。
  • 分布外数据：由训练后的(${\pi }_{\theta }$)生成的回答（图6中的绿色点）。
• 结果：在分布外数据上，($r_{\theta }$)表现出显著的长度偏见，奖励值与回答长度呈强正相关。通过线性回归分析，长度解释了分布外奖励方差的30-46%（以($R^2$)衡量，图6）。相比之下，分布内数据的奖励-长度相关性极弱甚至为负。

3.3 OOD引导的机制

论文将这种分布外长度偏见归因于“分布外引导”（OOD bootstrapping），其机制可以分解为以下几个方面：

1. 策略优化的动态：

   • DPO通过优化(${\mathcal{L}}_{\mathrm{DPO}}$)调整(${\pi }_{\theta }$)，使其更可能生成偏好回答(${\mathbf{y}}_w$)，同时减少非偏好回答(${\mathbf{y}}_l$)的概率。由于数据集($\mathcal{D}$)中偏好回答略长（表1），(${\pi }_{\theta }$)在优化过程中可能无意中放大这一微小偏见，倾向于生成更长的回答。
   • 随着训练进行，(${\pi }_{\theta }$)生成的回答逐渐偏离训练数据的长度分布（图2），进入分布外区域。这些长回答在隐式奖励函数($r_{\theta }$)下获得高分，进一步强化了生成长回答的倾向。

2. 隐式奖励的非线性放大：

   • 隐式奖励函数($r_{\theta }=\beta \log \frac{{\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})}{{\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})}$)依赖于(${\pi }_{\theta }$)的概率输出。由于语言模型的概率分布在高维空间中具有复杂性，(${\pi }_{\theta }$)在分布外区域的输出可能导致($r_{\theta }$)对某些特征（例如长度）的非线性放大。
   • 具体来说，(${\pi }_{\theta }$)可能对长回答分配过高的概率（因为训练数据中长回答略受偏好），从而使($r_{\theta }$)在分布外对长度产生强正相关。

3. 自增强循环：

   • DPO的优化是一个自增强过程：(${\pi }_{\theta }$)生成的长回答获得高奖励（通过($r_{\theta }$)），这反过来激励(${\pi }_{\theta }$)生成更长的回答。这种引导（bootstrapping）效应在分布外尤为显著，因为(${\pi }_{\theta }$)生成的回答不再受训练数据分布的约束。
   • 这种现象类似于传统RLHF中的奖励过优化，但DPO的隐式奖励函数使其表现更为隐晦。传统RLHF通过显式奖励模型和在线采样直接查询分布外数据，而DPO通过(${\pi }_{\theta }$)的优化动态间接引入分布外效应。

3.4 与传统RLHF的对比

在传统RLHF中，长度剥削被认为是奖励过优化的结果，源于以下机制：

• 奖励模型($r_{\varphi }$)在训练数据上学习到微小的长度偏见。
• 在强化学习阶段，策略(${\pi }_{\theta }$)通过在线采样生成分布外数据，奖励模型在这些数据上的预测可能放大长度偏见，导致策略生成越来越长的回答。

DPO没有显式奖励模型和在线采样，但隐式奖励函数($r_{\theta }$)和策略(${\pi }_{\theta }$)的联合优化同样导致了类似的现象。论文的发现表明，DPO的长度剥削不是简单的数据偏见问题，而是优化过程中分布外引导的动态结果。

4. 实验证据

论文通过以下实验进一步支持了OOD引导的解释：

• 长度分布分析（图2）：

  • 在HH和TL;DR数据集上，DPO生成的回答平均长度远超训练数据的偏好和非偏好回答。例如，DPO模型生成的回答长度是SFT模型的两倍，且显著偏离数据分布。
  • 降低($\beta$)（即允许更大的KL散度）会导致更严重的长度剥削，表明策略偏离参考分布加剧了分布外效应。

• 奖励-长度相关性（图6-8）：

  • 图6展示了隐式奖励($r_{\theta }$)在分布内和分布外的行为。分布内数据（偏好和非偏好回答）的奖励与长度几乎无关（甚至负相关），而分布外数据（DPO生成回答）的奖励与长度呈强正相关（($R^2=0.30-0.46$)）。
  • 图7和图8进一步分析了不同($\beta$)和正则化参数($\alpha$)下的结果，确认了分布外长度偏见的普遍性。

• 正则化效果（图3, 图5）：

  • 引入长度正则化（公式9）后，DPO生成的回答长度显著减少，且更接近SFT模型的分布。这表明正则化通过在隐式奖励中加入长度惩罚，抑制了分布外引导效应。
  • 正则化模型在训练过程中表现出更稳定的胜率提升（图5），避免了标准DPO因长度剥削导致的早期收敛。

5. 意义与启示

5.1 理论意义

这一发现揭示了DPO优化中的一个关键动态：即使仅使用离线数据，隐式奖励函数在分布外的行为也可能导致意外的偏见放大。长度剥削的OOD引导机制表明，DPO并非完全免疫传统RLHF的奖励过优化问题，只是其表现形式更隐晦。这种洞见为理解直接对齐算法的优化行为提供了新视角。

5.2 实际意义

• 开源模型改进：论文指出，长度剥削可能是开源模型在长度校正性能上落后于闭源模型的原因（图1）。通过正则化方法控制长度偏见，开源模型有望在自动评估中与闭源模型匹敌。
• 评估公平性：实验使用的GPT-4评判者本身具有长度偏见（Wang et al., 2023），这可能掩盖了DPO模型的真实性能。正则化方法通过减少长度剥削，使得模型性能更真实地反映质量而非长度。

5.3 未来研究方向

• 泛化到其他偏见：长度剥削只是DPO优化中可能出现的偏见之一。未来研究可以探索其他形式的分布外引导，例如风格或内容偏见。
• 规模律分析：论文的实验基于中小规模模型（Pythia 2.8B, Phi-2）。长度剥削在更大模型和更高质量数据集上的表现需要进一步研究。
• 其他直接对齐算法：DPO的OOD引导机制可能不适用于其他直接对齐算法（如ORPO或KTO），这些算法的优化动态值得进一步比较。

6. 结论

DPO中的长度剥削源于隐式奖励函数在分布外的引导效应。尽管训练数据中仅存在微小的长度偏见，DPO的优化过程通过策略(${\pi }_{\theta }$)的动态放大了这一偏见，导致生成冗长回答。隐式奖励函数在分布内对长度无明显偏见，但在分布外表现出强正相关，长度解释了30-46%的奖励方差。这一发现通过实验证据（如图2、图6-8）得到证实，并通过正则化方法得到缓解。理解和控制DPO中的OOD引导效应对于提升直接对齐算法的鲁棒性和性能至关重要。

后记

2025年4月19日于上海，在grok 3大模型辅助下完成。