【计算理论】计算复杂性 ( 证明团问题是 NP 完全问题 )

一、团问题是 NP 完全问题 证明思路

---

证明一个命题是 $\mathrm{N}\mathrm{P}$ 完全问题 :

① 证明是 $\mathrm{N}\mathrm{P}$ 问题 : 首先证明该问题是 $\mathrm{N}\mathrm{P}$ 问题 ;

② 证明是最难的 $\mathrm{N}\mathrm{P}$ 问题 : 然后证明所有的 $\mathrm{N}\mathrm{P}$ 问题 , 可以在多项式时间内规约到 该命题中 ; 也可以使用一个已经证明的 $\mathrm{N}\mathrm{P}$ 完全问题 , 在多项式时间内规约到 需要被证明的命题 ;

证明 团问题 是 $\mathrm{N}\mathrm{P}$ 完全的 , 从已知的 $\mathrm{N}\mathrm{P}$ 完全问题出发 , 已知的 $\mathrm{N}\mathrm{P}$ 完全问题就是 3-SAT 问题 ,

如果 3-SAT 问题是 $\mathrm{N}\mathrm{P}$ 完全的话 ,

只要证明 3-SAT 问题 可以在 多项式时间内规约 到 团问题 中 , 3-SAT $\le$ 团问题 ,

就可以证明 团问题 是 $\mathrm{N}\mathrm{P}$ 完全问题 ;

将 3-SAT 问题 可以在 多项式时间内规约 到 团问题 中 ,

给定一个 3-SAT 问题 的 布尔逻辑公式 ,

$\varphi =({\mathrm{x}}_1\vee {\mathrm{x}}_1\vee {\mathrm{x}}_2)\wedge (\overline{{\mathrm{x}}_1}\vee \overline{{\mathrm{x}}_2}\vee \overline{{\mathrm{x}}_2})\wedge (\overline{{\mathrm{x}}_1}\vee {\mathrm{x}}_2\vee {\mathrm{x}}_2)$

构造一个 无向图 ,

使得 布尔逻辑公式 是可满足的 , 当且仅当 , 无向图中有一个 $\mathrm{k}$ 团 ;

$\mathrm{k}$ 团就是无向图中 $\mathrm{k}$ 个节点子集 , 每两个节点之间都有边相连 ;

证明过程 : 从 给定的 3-SAT 布尔逻辑公式 $\varphi =({\mathrm{x}}_1\vee {\mathrm{x}}_1\vee {\mathrm{x}}_2)\wedge (\overline{{\mathrm{x}}_1}\vee \overline{{\mathrm{x}}_2}\vee \overline{{\mathrm{x}}_2})\wedge (\overline{{\mathrm{x}}_1}\vee {\mathrm{x}}_2\vee {\mathrm{x}}_2)$ 中 , 构造出一个无向图 出来 , 使得该无向图可以满足 " 布尔逻辑公式 是可满足的 , 当且仅当 , 无向图中有一个 $\mathrm{k}$ 团 "

二、证明团问题是 NP 完全问题

---

参考上篇博客 【计算理论】计算复杂性 ( 3-SAT 是 NP 完全问题 | 团问题是 NP 完全问题 | 团问题是 NP 完全问题证明思路 ) 三、团问题是 NP 完全问题 证明思路

从 给定的 3-SAT 布尔逻辑公式 $\varphi =({\mathrm{x}}_1\vee {\mathrm{x}}_1\vee {\mathrm{x}}_2)\wedge (\overline{{\mathrm{x}}_1}\vee \overline{{\mathrm{x}}_2}\vee \overline{{\mathrm{x}}_2})\wedge (\overline{{\mathrm{x}}_1}\vee {\mathrm{x}}_2\vee {\mathrm{x}}_2)$ 中 , 构造出一个无向图 出来 , 使得该无向图可以满足 " 布尔逻辑公式 是可满足的 , 当且仅当 , 无向图中有一个 $\mathrm{k}$ 团 "

构造点集三元组 : 给定 3-SAT 合取范式 , 布尔逻辑公式中 , 每个子项都有一个三元组 ,

上图中的 无向图 左侧的 点集三元组 对应 布尔逻辑公式 合取范式 中的 $({\mathrm{x}}_1\vee {\mathrm{x}}_1\vee {\mathrm{x}}_2)$ 子项 ,

上图中的 无向图 顶部的 点集三元组 对应 布尔逻辑公式 合取范式 中的 $(\overline{{\mathrm{x}}_1}\vee \overline{{\mathrm{x}}_2}\vee \overline{{\mathrm{x}}_2})$ 子项 ,

上图中的 无向图 右侧的 点集三元组 对应 布尔逻辑公式 合取范式 中的 $(\overline{{\mathrm{x}}_1}\vee {\mathrm{x}}_2\vee {\mathrm{x}}_2)$ 子项 ,

构造无向边 : 对于布尔逻辑公式 , 3-SAT 公式 ,

$\varphi =({\mathrm{x}}_1\vee {\mathrm{x}}_1\vee {\mathrm{x}}_2)\wedge (\overline{{\mathrm{x}}_1}\vee \overline{{\mathrm{x}}_2}\vee \overline{{\mathrm{x}}_2})\wedge (\overline{{\mathrm{x}}_1}\vee {\mathrm{x}}_2\vee {\mathrm{x}}_2)$

如果要取值为真 , 需要每个子项取值都为真 ,

如果每个子项为真 , 每个子项都是析取式 , 只要保证每个子项中至少有一个为真即可 ,

在每个子项中取一个 词 为真的值 , 词的取值互相之间不发生矛盾 , 不能出现有一个词 是另外一个词的否定 , 词就是 原子命题变元 或其否定 ;

${\mathrm{x}}_1$ 与 $\overline{{\mathrm{x}}_1}$ 互为否定 , 这两个节点之间不能有边相连 ,

${\mathrm{x}}_2$ 与 $\overline{{\mathrm{x}}_2}$ 互为否定 , 这两个节点之间不能有边相连 ,

无向边构造原则 : 不同的 $3$ 组点集之间 , 如果不是互为否定的 , 就连接一条边 , 本组之间没有边 ;

下图是构造好的无向图 :

证明 布尔逻辑公式 $\varphi =({\mathrm{x}}_1\vee {\mathrm{x}}_1\vee {\mathrm{x}}_2)\wedge (\overline{{\mathrm{x}}_1}\vee \overline{{\mathrm{x}}_2}\vee \overline{{\mathrm{x}}_2})\wedge (\overline{{\mathrm{x}}_1}\vee {\mathrm{x}}_2\vee {\mathrm{x}}_2)$ 是可满足的 , 当且仅当 , 无向图中有一个 $3$ 团 ;

取值 :

${\mathrm{x}}_1=\mathrm{f}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e},\overline{{\mathrm{x}}_1}=\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}$

${\mathrm{x}}_2=\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e},\overline{{\mathrm{x}}_2}=\mathrm{f}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e}$

${\mathrm{x}}_1\vee {\mathrm{x}}_1\vee {\mathrm{x}}_2=\mathrm{f}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e}\vee \mathrm{f}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e}\vee \mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}=\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}$

$\overline{{\mathrm{x}}_1}\vee \overline{{\mathrm{x}}_2}\vee \overline{{\mathrm{x}}_2}=\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}\vee \mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}\vee \mathrm{f}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e}=\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}$

$\overline{{\mathrm{x}}_1}\vee {\mathrm{x}}_2\vee {\mathrm{x}}_2=\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}\vee \mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}\vee \mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}=\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}$

上述取值时 , 合取范式中每个子项都为真 , 布尔逻辑公式取值为真 ;

找 $3$ 团 : 在无向图中 , 找到一个 $3$ 团 , 下图中红色的点组成的集合就是一个 $3$ 团 , 可以发现取值为真的点都可以组成一个 $3$ 团 ;

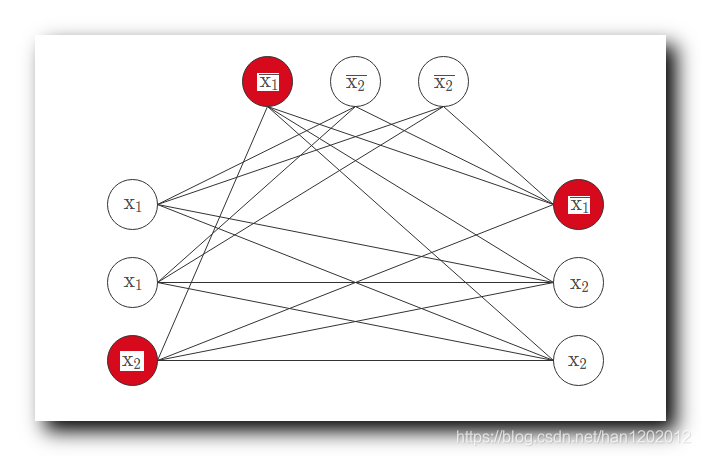
上图中 $3$ 团 的规律就是找到 $3$ 个取值为真的赋值 , 就可以自动找到一个 $3$ 团 ;