1.矩阵分解(MF)
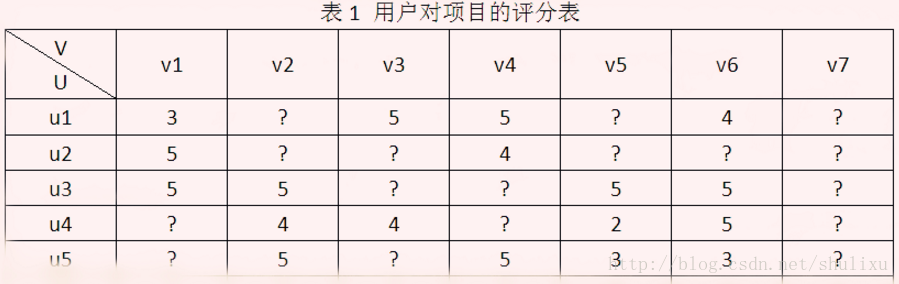
目前推荐系统中用的最多的就是矩阵分解方法,在Netflix Prize推荐系统大赛中取得突出效果。以用户-项目评分矩阵为例,矩阵分解就是预测出评分矩阵中的缺失值,然后根据预测值以某种方式向用户推荐。常见的矩阵分解方法有基本矩阵分解(basic MF),正则化矩阵分解)(Regularized MF),基于概率的矩阵分解(PMF)等。
利用代数中SVD方法对矩阵进行分解。奇异值分解首先需要对评分矩阵进行补全,比如用全局平均值或用户、物品平均值进行补全。然后对补全之后的矩阵进行SVD分解从而将高维评分矩阵分解成低维的U,I矩阵。但是这种方法有两个问题:一是补全后的矩阵是一个稠密矩阵,存储需要很大空间。二是SVD计算复杂度很高。
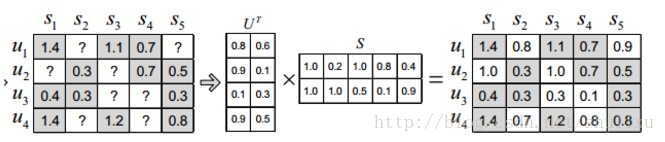
Basic MF最基础的分解方式,将评分矩阵R分解为用户矩阵U和项目矩阵S, 通过不断的迭代训练使得U和S的乘积越来越接近真实矩阵,矩阵分解过程如图:
预测值接近真实值就是使其差最小,这是我们的目标函数,然后采用梯度下降的方式迭代计算U和S,它们收敛时就是分解出来的矩阵。我们用损失函数来表示误差(等价于目标函数):
R_ij是评分矩阵中已打分的值,U_i和S_j相当于未知变量。为求得公式1的最小值,相当于求关于U和S二元函数的最小值(极小值或许更贴切)。通常采用梯度下降的方法:
yita是学习速率,表示迭代的步长。其值为1.5时,通常以震荡形式接近极值点;若<1迭代单调趋向极值点;若>2围绕极值逐渐发散,不会收敛到极值点。具体取什么值要根据实验经验,另外还需要在每一步对学习速率进行衰减,目的是使算法尽快收敛。该方法也叫LFM(latent factor model).考虑偏置项的LFM。 在原有分解的基础上加入全局平均数,用户偏置项和item偏置项。(biassvd)
- 考虑邻域影响的LFM。 在上一个基础上加上基于邻域方法(svd++)
- 正则化矩阵分解是Basic MF的优化,解决MF造成的过拟合问题。其不是直接最小化损失函数,而是在损失函数基础上增加规范化因子,将整体作为损失函数。Regularized MF
- 其中
- 梯度下降结束条件:f(x)的真实值和预测值小于自己设定的阈值
PMF(概率矩阵分解)
RegularizedMF是对BasicMF的优化,而PMF是在RegularizedMF的基础上,引入概率模型进一步优化。假设用户U和项目V的特征矩阵均服从高斯分布,通过评分矩阵已知值用MAP(最大后验概率)和MLE(最大似然估计)(下面会详细说明)得到U和V的特征矩阵,然后用特征矩阵去预测评分矩阵中的未知值。

首先通过极大似然估计U,V



也就是说我们这里只考虑最大化分子,因为分母是一个定值。

解传统矩阵分解可以采用各种优化方法,对于概率分解,由于最后求的是参数U和V的最大似然估计,因此可以用最大期望法(EM)和马尔可夫链蒙特卡罗算法(MCMC)。
PMF也有改进的地方,它没有考虑到评分过程中用户的个人信息,比如有的用户就是喜欢打低分,有的项目(电影)质量就是不高,分肯定高不了等,这样可以采用加入偏置的概率矩阵分解(贝叶斯概率矩阵分解BPMF)
对比:





 本文深入介绍了推荐系统中常用的矩阵分解技术,包括基本矩阵分解、正则化矩阵分解及基于概率的矩阵分解等方法,并探讨了如何通过这些技术预测用户评分矩阵中的缺失值,进而实现个性化推荐。
本文深入介绍了推荐系统中常用的矩阵分解技术,包括基本矩阵分解、正则化矩阵分解及基于概率的矩阵分解等方法,并探讨了如何通过这些技术预测用户评分矩阵中的缺失值,进而实现个性化推荐。
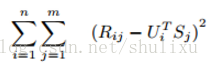
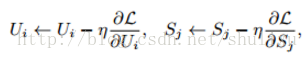
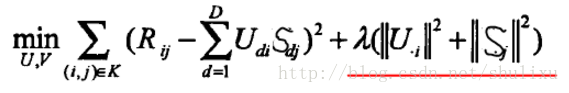
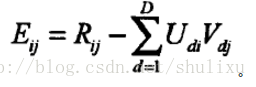

















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








