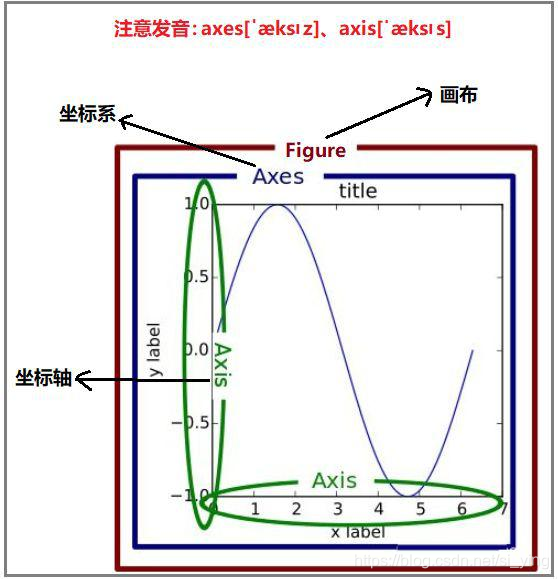
1 注意点
2 完整代码
import numpy as np
import matplotlib.pyplot as plt
def calc_abc_from_line_2d(x0, y0, x1, y1):
a = y0 - y1
b = x1 - x0
c = x0*y1 - x1*y0
return a, b, c
def get_line_cross_point(line1, line2):
a0, b0, c0 = calc_abc_from_line_2d(*line1)
a1, b1, c1 = calc_abc_from_line_2d(*line2)
D = a0 * b1 - a1 * b0
if D == 0:
return None
x = (b0 * c1 - b1 * c0) / D
y = (a1 * c0 - a0 * c1) / D
return x, y
r = 1
a, b = (0., 0.)
theta2 = 0.8 * np.pi
angle1 = np.pi - theta2
rushedianx = a + r * np.cos(theta2)
rushediany = b + r * np.sin(theta2)
n = 1.3
angle2 = angle1 / n
fig = plt.figure()
axes = fig.add_subplot(111)
axes.axis('equal')
theta = np.arange(0, 2 * np.pi, 0.01)
x = a + r * np.cos(theta)
y = b + r * np.sin(theta)
axes.plot(x, y, color='black')
x2 = [rushedianx - 0.6, rushedianx]
y2 = [rushediany, rushediany]
axes.plot(x2, y2, color='black')
axes.arrow(x2[0], y2[0], 0.25, 0, head_width=0.05, head_length=0.1, fc='k', ec='k')
x3 = [0, rushedianx]
y3 = [0, rushediany]
axes.plot(x3, y3, color='black')
k = rushediany / rushedianx
axes.plot([rushedianx - 0.5, rushedianx], [rushediany - 0.5 * k, rushediany], c='k', linestyle='--')
x4 = [rushedianx, rushedianx + 2.7]
y4 = [rushediany, rushediany]
axes.plot(x4, y4, color='black',linestyle='--')
angle3 = angle1-angle2
x5 = [rushedianx, rushedianx + 1.77 * r * np.cos(angle3)]
y5 = [rushediany, rushediany - 1.77 * r * np.sin(angle3)]
axes.plot(x5, y5, color='black')
angle4 = 2 * angle2 - angle1
axes.plot([0, a + 1.74 * r * np.cos(angle4)], [0, b + 1.74 * r * np.sin(angle4)], c='k', linestyle='--')
fanshedianx = a + r * np.cos(angle4)
fanshediany = b + r * np.sin(angle4)
angle5 = 2 * angle2 - angle3
chushedianx = fanshedianx - 1.77 * r * np.cos(angle5)
chushediany = fanshediany - 1.77 * r * np.sin(angle5)
x6 = [fanshedianx, chushedianx]
y6 = [fanshediany, chushediany]
axes.plot(x6, y6, color='black')
x7 = [a + 1.74 * r * np.cos(angle4), chushedianx]
y7 = [b + 1.74 * r * np.sin(angle4), chushediany]
axes.plot(x7, y7, color='black', linestyle='--')
k2 = (y7[1] - y7[0]) / (x7[1] - x7[0])
x8 = [chushedianx, 0]
y8 = [chushediany, 0]
axes.plot(x8, y8, color='black')
axes.arrow(chushedianx, chushediany, -0.3, -0.3 * k2, head_width=0.05, head_length=0.1, fc='k', ec='k')
xstart = rushedianx
xend = a + 1.74 * r * np.cos(angle4)
x9 = [0, 0]
y9 = [rushediany, 0]
i = xstart
while i < xend:
x9[0] = i
line1 = [x9[0], y9[0], x9[0] - 0.1, y9[0] - 0.1]
line2 = [fanshedianx, fanshediany, rushedianx, rushediany]
line3 = [0, 0, fanshedianx, fanshediany]
p1, p2 = get_line_cross_point(line1, line2)
p3, p4 = get_line_cross_point(line1, line3)
if(p2 > p4):
x9[1] = p1
y9[1] = p2
else:
x9[1] = p3
y9[1] = p4
axes.plot(x9, y9, color='black')
i += 0.1
theta3 = np.arange(-angle1, -angle3, 0.01)
jiaox = rushedianx + 0.2 * np.cos(theta3)
jiaoy = rushediany + 0.2 * np.sin(theta3)
axes.plot(jiaox, jiaoy, color='black')
font={'family':'Times New Roman',
'style':'italic',
'weight':'bold',
'color':'black',
'size':20
}
plt.text(-1.3, 0.34,"S", fontdict=font)
plt.text(-0.9, 0.7, "A", fontdict=font)
plt.text(-1.3, 0.65, "i", fontdict=font)
plt.text(-0.1, 1.2, "i-r", fontdict=font)
plt.text(-0.42, 0.35, "r", fontdict=font)
x10 = [-0.5, 0]
y10 = [b + r * np.sin(theta2), 1.15]
axes.plot(x10, y10, color='black')
plt.axis('off')
plt.show()
3 运行结果
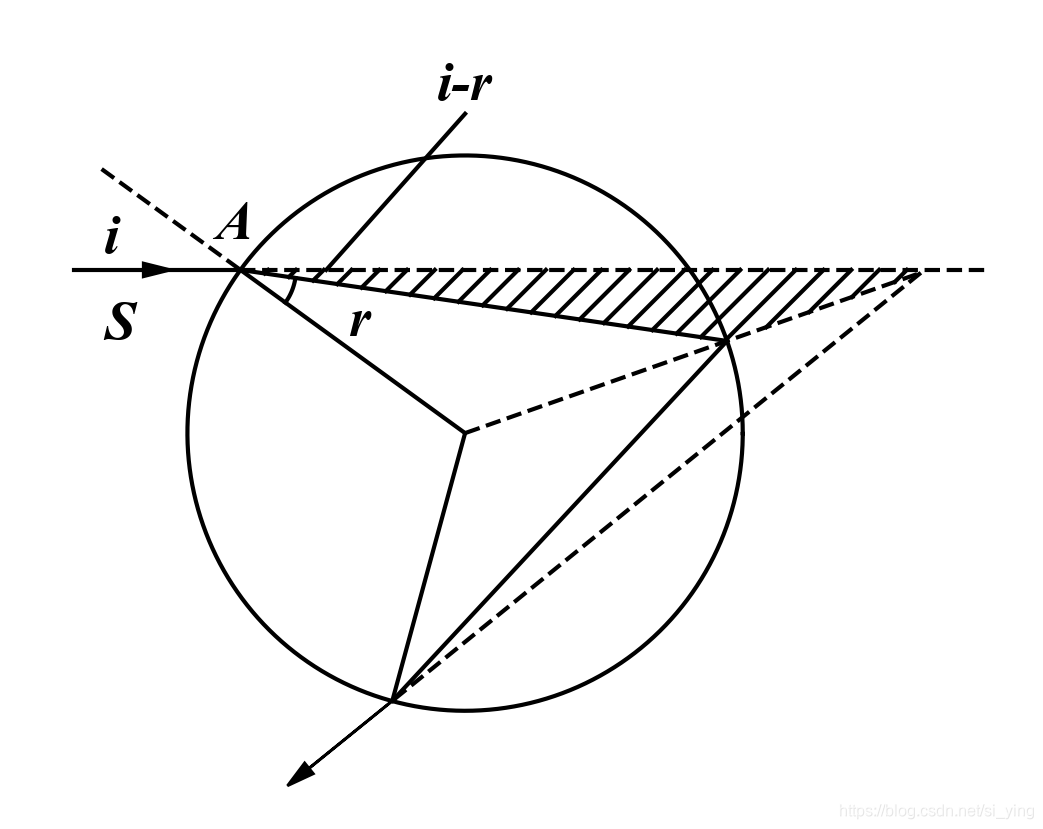










 本文介绍了使用Python进行水滴折射模拟的注意事项、完整代码及运行结果展示,通过代码实现光线在水滴中的传播和折射效果。
本文介绍了使用Python进行水滴折射模拟的注意事项、完整代码及运行结果展示,通过代码实现光线在水滴中的传播和折射效果。















 906
906

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










