【数据结构】图论

图论

Graph Theory

---

#1 关于“图”

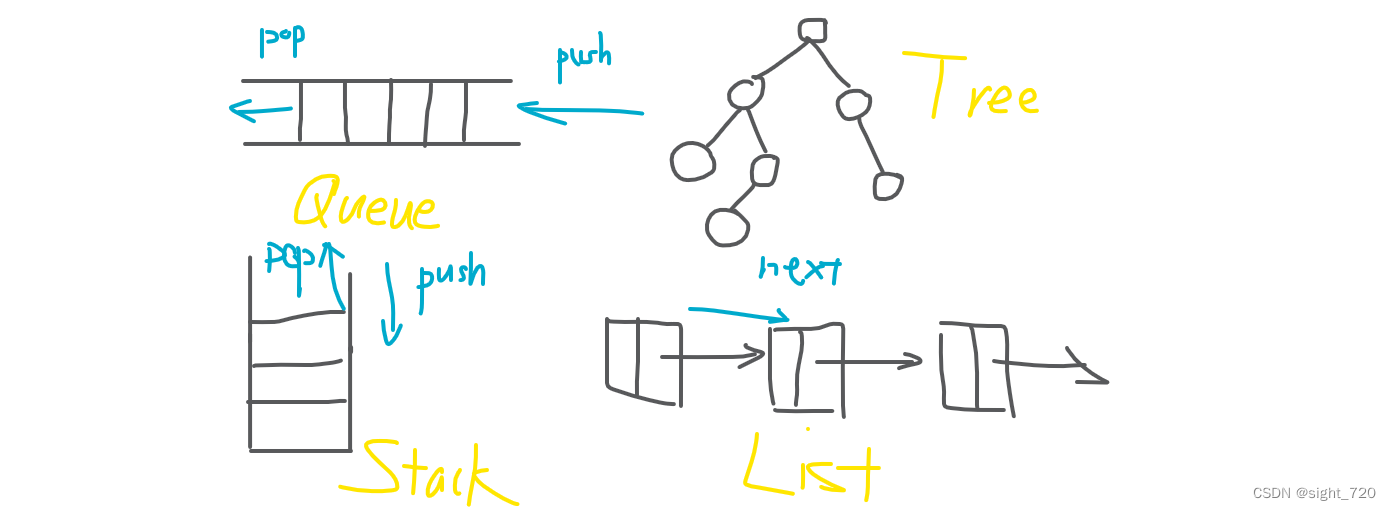
图也是一种数据结构。不同于线性的队列、栈、链表、Hash 表以及树形的树、堆等基本数据结构，图长这个样子：

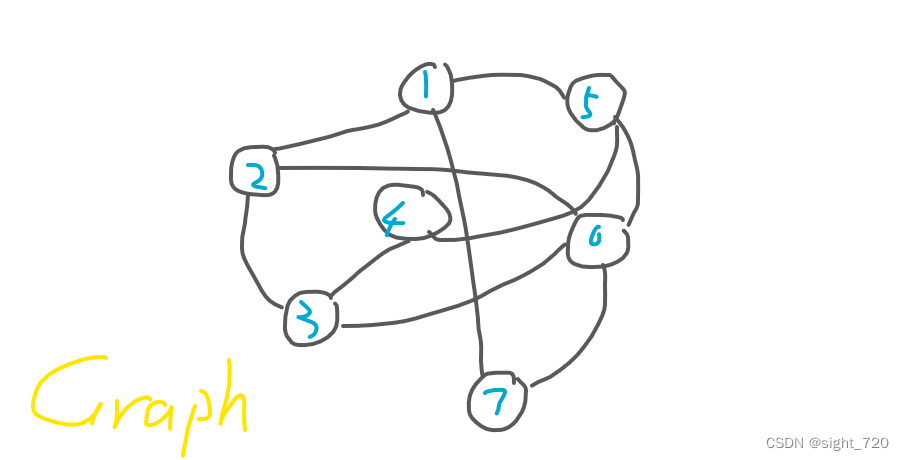
其实容易发现，有时候把图拎起来，它就变成了一棵树。

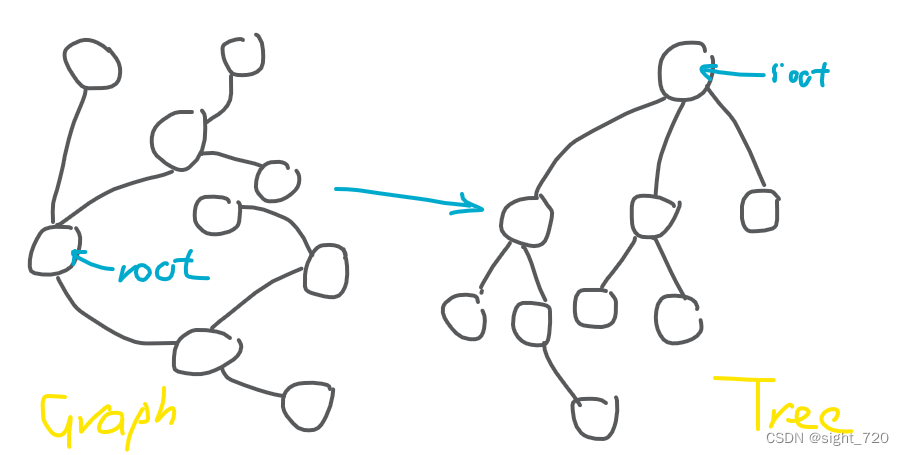
但有时候却不行。所以图凭什么特殊？它和树有什么区别？凭什么它能成为一种独立的数据结构？我们先说说图的定义。

图 $(Graph)$ 是描述于一组对象的结构，其中某些对象对在某种意义上是“相关的”。

这点不难理解。家谱树就是一个很好的例子。直观一点的定义是：

图是一个有序二元组 $(V,E)$，其中 $V$ 被称为顶集 $(VerticesSet)$，$E$ 被称为边集 $(EdgeSet)$ 。

简单说，图是由点和线组成的。点就是事物，线就是事物之间的联系。

图的概念可见 百度百科-图 。

接着就可以回答之前的问题了：它和树有什么区别？

树是 连通且无环 的无向图。因此树是一种特殊的图。

---

#2 图的存储

计算机中的图并不像我们做几何题时的图一样，而是将其用数组或 STL 模拟。

---

a) 邻接矩阵

这是最原始的存图方法。定义二维数组 $G$，$G_{i,j}$ 有值（不需要存边权时为 $1$，也可以存边权）说明 $i$ 到 $j$ 有路，反之没路。

int G[...][...];
for(int i = 1; i <= n; i++) {
	int u, v;
	scanf("%d%d", &u, &v);
	G[u][v] = G[v][u] = 1;
} //无向图

int G[...][...];
for(int i = 1; i <= n; i++) {
	int u, v;
	scanf("%d%d", &u, &v);
	G[u][v] = 1;
} //有向图（且u指向v)

int G[...][...];
for(int i = 1; i <= n; i++) {
	int u, v, w;
	scanf("%d%d%d", &u, &v, &w);
	G[u][v] = G[v][u] = w;
} //带边权的无向图（有向图同理)

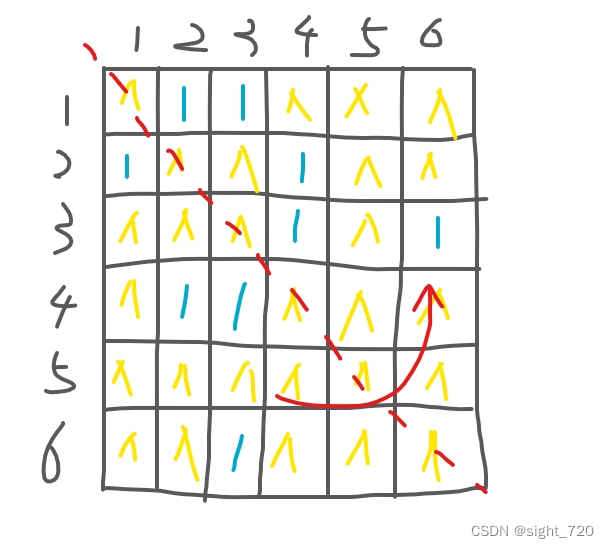
无向图的邻接矩阵沿左对角线对称。

缺点：表示稀疏图时，浪费大量内存空间；一般情况下无法存储重边。
优点：在常数时间内判断两点之间是否有边存在；代码量少。

---

b) 邻接表

对于每一个节点，都可以存储其相邻的节点信息。可以想到用数组存储。

以无权无向图为例：

struct node {
	int k, a[...]; //k是相邻节点数
} G[...];
...
for(int i = 1; i <= m; i++) {
	int u, v;
	scanf("%d%d", &u, &v);
	G[u].k++;
	G[v].k++;
	G[u].a[G[u].k] = v;
	G[v].a[G[v].k] = u;
}

其实，使用 $vector$ 会更加简洁：

vector<int> G[...];
...
for(int i = 1; i <= m; i++) {
	int u, v;
	scanf("%d%d", &u, &v);
	G[u].push_back(v);
	G[v].push_back(u);
}

这就是我们经常看到的邻接表。如下图：

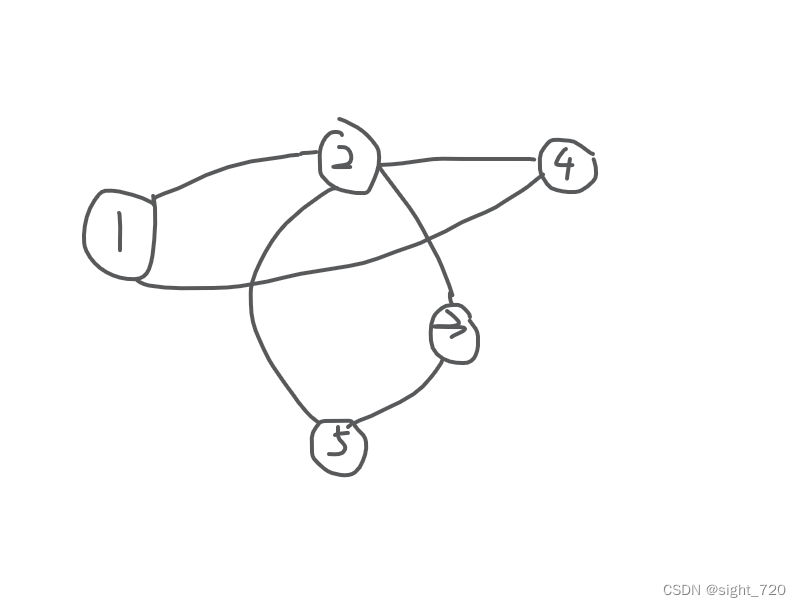
使用邻接表存储后：

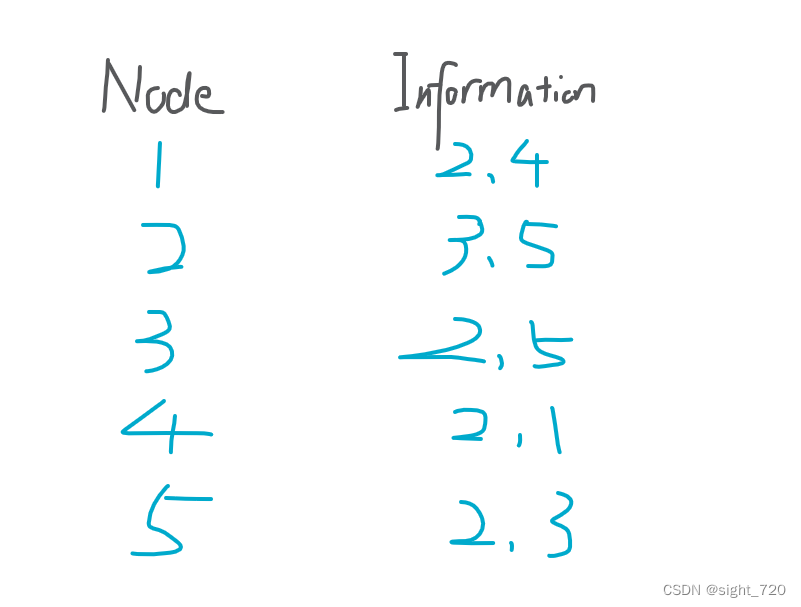
上面介绍的是面对无权图的邻接表。如果图为有权图，邻接表似乎没有地方存储边权。但结构体为我们开辟了新的存储空间。

struct node {
	int v, w; //v是边的终点，w是边权
};
vector<node> G[...];
...
for(int i = 1; i <= m; i++) {
	int u, v, w;
	scanf("%d%d%d", &u, &v, &w);
	G[u].push_back((node){v, w});
	G[v].push_back((node){u, w});
}

缺点：访问和修改慢。
优点：存储效率非常高；空间复杂度优；可以存储重边。

---

c) 链式前向星

之前我们所提到的两种存图方式终点在于一个字：邻，通过存储相邻 节点 的信息构造出一整张图。而链式前向星提供了一种相似却不相同的思路。链式前向星的实现类似于链表，一个节点既存储数据有存储指针。

int Head[...], Edge[...], Vertex[...], Next[...], cnt;
void AddEdge(int u, int v, int w) {
	cnt++;
	Vertex[cnt] = v;
	Edge[cnt] = w;
	Next[cnt] = Head[u];
	Head[u] = cnt;
}
...
for(int i = 1; i <= m; i++) {
	int u, v, w;
	scanf("%d%d%d", &u, &v, &w);
	AddEdge(u, v, w);
	AddEdge(v, u, w);
}

链式前向星最难理解的地方在于，这几个数组到底是什么意思。在函数 $AddEdge$ 中，形参 $u$ 为一条边的起点，$v$ 为一条边的终点，$w$ 为一条边的边权。会发现，链式前向星不同于邻接矩阵和邻接表去存储 节点 信息，而是存储一条 边 的信息。$cnt$ 的作用便是指示这是第几条边。数组 $Vertex$ 和 $Edge$ 一目了然，分别代表第 $cnt$ 条边的终点与边权。那么数组 $Head$ 与 $Next$ 呢？这两个数组似乎不知所云。

事实上，数组 $Head$ 存储的是 第 $cnt$ 条边的起点的第一条边的位置，而 $Next$ 存储的是 第 $cnt$ 条边的下一条边的位置。

还是拿这个图为例：

链式前向星存储后：

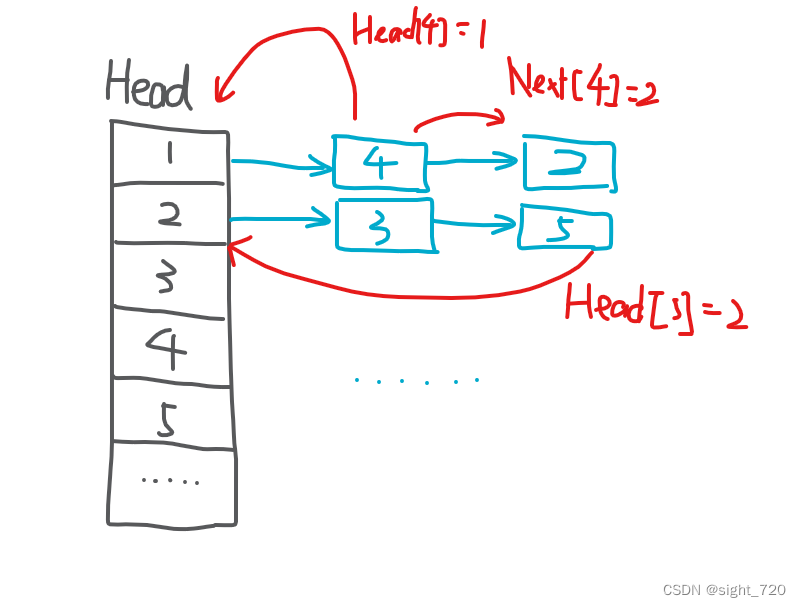
故，数组 $Vertex$ 与 $Edge$ 存储边的信息（数据），数组 $Head$ 与 $Next$ 存储边的位置（指针）。

缺点：不能直接找到两点之间是否有边；不支持直接排序。
优点：可以应对点非常多的情况；可以存储重边。

以上三种存图方式为近年来所流行，尤其为邻接表和链式前向星。但在不同的题目中三种都有各自的优势，不能一味否定，也不能加以吹捧。正如 GM 所说：

“各有千秋。”

---

#3 图论 | 最短路

最短路在生活中的应用很多，因为人人都想要像光一样走直线。但很多时候这是不可能的，有时绕点弯路反而最划算。这也导致最短路成为了图论里最有代表性的版块。

对于最短路，可以分为两种：多源最短路 以及 单源最短路。

---

a) 多源最短路

所谓多源，即谓某算法可求出任意两点间最短路长度。

1.Floyd 算法

该算法以图灵奖得主 Robert W．Floyd 命名。本质上是动态规划。

定义状态 $di{s}_{k,i,j}$ 为 经过若干个编号不超过 $k$ 的节点，从 $i$ 至 $j$ 的最短路长度。

值得注意的是 $di{s}_{k,i,j}$ 并不代表经过 $k$ 一个点，而是若干个不超过 $k$ 的点！

那么最短路问题即可分成两个子问题：经过编号不超过 $k-1$ 的节点从 $i$ 至 $j$ 的最短路距离，和从 $i$ 至 $j$ 中间经过 $k$（从 $i$ 至 $k$ 再到 $j$）的距离。即

$$di{s}_{k,i,j}=\min (di{s}_{k-1,i,j},di{s}_{k-1,i,k}+di{s}_{k-1,k,j})$$

初值 $di{s}_{0,i,j}=G_{i,j}$ ，其中 $G_{i,j}$ 为邻接矩阵。

在 Floyd 算法的执行过程中，其本质是动态规划，$k$ 即为 阶段，因而 $k$ 的循环必须置于最外层。

对 Floyd 的状态转移方程研究可得，$k$ 这一维并无作用，可以省略。

$$di{s}_{i,j}=\min (di{s}_{i,j},di{s}_{i,k}+di{s}_{k,j})$$

初值为 $di{s}_{i,j}=G_{i,j}$，$G_{i,j}$ 为邻接矩阵。

以有权无向图为例：

#define inf 0x3f3f3f3f
int dis[...][...];
void SetUp() { //初始化
	for(int i = 0; i <= n; i++) {
		for(int j = 0; j <= n; j++) dis[i][j] = inf; //只要i,j间没有边便置为极大值，求最短路时便不会将其选中
		dis[i][i] = 0; //自己到自己肯定为0
	}
}
void Floyd() {
	for(int k = 1; k <= n; k++) {
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= n; j++) {
				if(dis[i][j] > dis[i][k] + dis[k][j]) dis[i][j] = dis[i][k] + dis[k][j];
			}
		}
	}
}
...
SetUp();
for(int i = 1; i <= m; i++) {
	int u, v, w;
	scanf("%d%d%d", &u, &v, &w);
	dis[u][v] = dis[v][u] = w; //用dis数组代替邻接矩阵
}
Floyd();

最终 $di{s}_{i,j}$ 就是 $i$ 到 $j$ 的最短路长度。

时间复杂度：$O(n^3)$
空间复杂度：$O(n^2)$

优点：可求多源最短路；代码量少；易理解；可处理负权图。
缺点：时间复杂度过高，局限性强。

---

b) 单源最短路

指某算法可求出指定点到任意点的最短路长度（与多源相对）。

---

1.Dijkstra 算法

该算法由 Edsger Wybe Dijkstra 于 1959 年提出。本质上是贪心。

引入新概念：松弛。

假如你有一根橡皮筋：

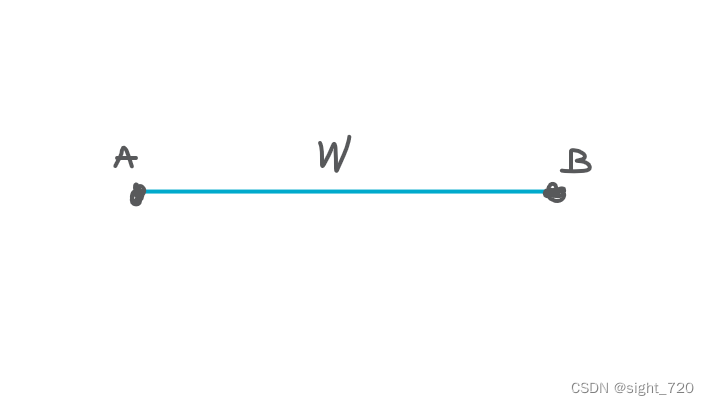
这时出现了一个点，将橡皮筋勒在该点上，使得橡皮筋的长度更短（不要疑惑），使其更加“松弛”，这步操作便称为 松弛操作。

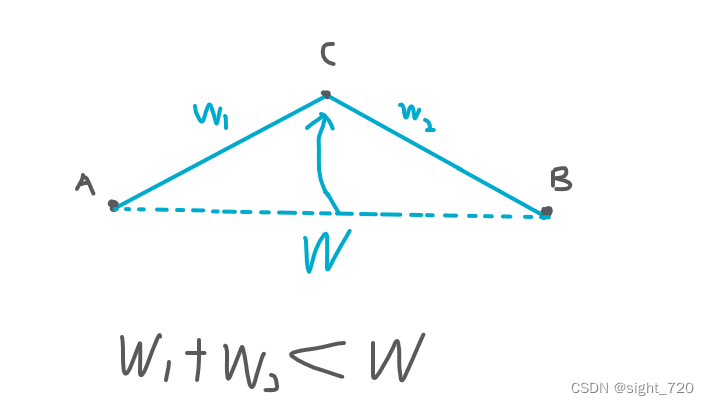
很明显上图违反了三角形三边的关系。似乎松弛操作违反了常理，但实则不然。生活中的橡皮筋只存在距离一种边权，而在图论中则不止。比如去某地，有一条直达的路，有一条迂回的路。正常时一定会选择直达的路，因为速度不变路程与时间成反比。但如果人人都这么想，都走直达的路，导致堵得水泄不通，这时走迂回的路也是不错的选择——这就是我们前面所提到的走弯路反而划算的情况。简单说，局部最优解不等于全局最优解。

这也顺便揭示了一个道理：

一时的得，不是永远；一时的失，不是未来。

扯远了

定义 $di{s}_i$ 表示起点 $s$ 到点 $i$ 的最短路长度。

Dijkstra 算法的核心便在于松弛。将点分为蓝白两大阵营，蓝阵营中是已经经过松弛操作确定最短路的点，而白阵营则是没有的。步骤如下：

1.在没有被访问过的点（白）中找一个相邻顶点 $k$，使得 $di{s}_k$ 是最小的。
2.将 $k$ 放进蓝阵营中，即 $vi{s}_k=1$。
3.更新与 $k$ 相连的每个未确定最短路径（白）的顶点 $v$，进行松弛操作。

if(dis[v] > dis[k] + w[v][k]) dis[v] = dis[k] + w[v][k]; //w[v][k]为v,k之间边权。

#define inf 0x3f3f3f3f
void SetUp() {
	for(int i = 0; i <= ...; i++) dis[i] = inf;
	for(int i = 0; i <= ...; i++) vis[i] = 0;
}
void Dijkstra(int s) {
	SetUp();
	dis[s] = 0;
	for(int i = 1; i <= n; i++) {
		int u, v, w, MIN = inf;
		for(int j = 1; j <= n; j++) {
			if(dis[i] < MIN && !vis[i]) u = i, MIN = dis[i];
		}
		vis[u] = 1;
		for(int i = Head[u]; i; i = Next[i]) { //链式前向星
			v = Vertex[i];
			w = Edge[i];
			if(dis[v] > dis[u] + w) dis[v] = dis[u] + w;
		}
	}
}
		

时间复杂度：$O(n^2)$
空间复杂度：$O(n)$

优点：空间复杂度低；易理解。
缺点：负权图无法处理；时间复杂度较高。

---

2.堆优化 Dijkstra 算法

Dijkstra 循环内的第一层循环的作用是寻找最小的 $dis$ 值，于是可以用堆进行优化。

struct node {
	int u, w;
	node(int _u, int _w) { u = _u, w = _w; }
	friend bool operator<(node x, node y) { return x.w > y.w; }
};
priority_queue<node> pq;
...
void SetUp() {
	for(int i = 0; i <= ...; i++) dis[i] = inf;
	for(int i = 0; i <= ...; i++) vis[i] = 0;
}
void Dijkstra(int s) {
	SetUp();
	dis[s] = 0;
	pq.push(node(s, 0));
	while(!pq.empty()) {
		int u = pq.top().u;
		pq.pop();
		if(vis[u]) continue;
		vis[u] = 1;
		for(int i = Head[u]; i; i = Next[i]) {
			int v = Vertex[i];
			int w = Edge[i];
			if(dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				pq.push(node(v, dis[v]));
			}
		}
	}
}

时间复杂度：$\approx O(m\log n)$
空间复杂度：$O(n)$

优点：在稠密图的处理上时间复杂度低；空间复杂度低。
缺点：负权图无法处理。

---

3.Bellman-Ford 算法

由 Richard Bellman 和 Lester Ford 共同提出。

原理为对图进行最多 $n-1$ 次松弛操作，每次操作对所有的边进行松弛，求出最短路。

Bellman-Ford 与 Dijkstra 最大的区别在于 Bellman-Ford 可以处理负权图，可以判断图中是否存在负环。

void SetUp() {
	for(int i = 1; i <= 500; i++) dis[i] = inf;
}
bool BellmanFord(int s) {
	SetUp();
	dis[s] = 0;
	for(int i = 1; i <= n - 1; i++) { //i只用于控制循环次数
		for(int j = 1; j <= m; j++) {
			if(dis[v[j]] > dis[u[j]] + w[j]) dis[v[j]] = dis[u[j]] + w[j]; //松弛
		}
	}
	for(int i = 1; i <= m; i++) {
		if(dis[v[i]] > dis[u[i]] + w[i]) return 0; //0是有负环
	}
	return 1; //1是无负环
}
...
for(int i = 1; i <= m; i++) {
	scanf("%d%d%d", &u[i], &v[i], &w[i]);
}

那么判断负环的原理是什么？

首先我们知道负环的特点是进入后产生死循环：

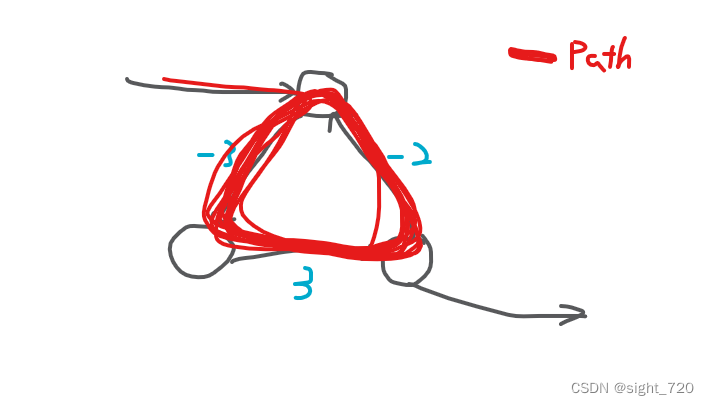
所以只要在程序执行过程中出现死循环，说明该图含有负环。

在 $n-1$ 次迭代后强制终止程序，此时若图中无负环，所有的边都应该已经经过松弛操作。若有负环，程序将会反复在负环中进行松弛操作，导致后面的边无法被执行松弛操作。故若图中每条边都不能被松弛（满足三角形不等式），说明无负环，反之存在。

时间复杂度：$O(mn)$
空间复杂度：$O(n)$

优点：空间复杂度低；可处理负权图。
缺点：时间复杂度较高。

4.SPFA 算法

国内惯用 SPFA，全称 Shortest Path Fast Algorithm，国际上称作 Bellman-Ford using queue optimization（Bellman-Ford 的队列优化形式），段凡丁于 1994 年提出（国际上并不承认）。

在 Bellman-ford 算法中，有许多松弛是无效的。这便是 SPFA 算法出现的原因。SPFA 算法先将源点加入队列。然后从队列中取出一个点(此时该点为源点)，对该点的邻接点进行松弛，如果该邻接点松弛成功且不在队列中，则把该点加入队列。如此循环往复，直到队列为空，则求出了最短路径。

void SetUp() {
	for(int i = 0; i <= ...; i++) vis[i] = 0;
	for(int i = 0; i <= ...; i++) dis[i] = inf;
	for(int i = 0; i <= ...; i++) cnt[i] = 0;
}
bool SPFA(int s) {
	queue<int> q;
	SetUp();
	vis[s] = 1, dis[s] = 0;
	q.push(s);
	while(!q.empty()) {
		int u = q.front();
		q.pop();
		vis[u] = 0;
		for(int i = Head[u]; i; i = Next[i]) {
			int v = Vertex[i];
			int w = Edge[i];
			if(dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				if(!vis[v]) {
					vis[v] = 1;
					cnt[v]++;
					if(cnt[v] == n) return 0;
					else q.push(v);
				}
			}
		}
	}
}

SPFA 算法同样可以判断负环，当一个节点入队次数超过 $n$ 次时，说明程序已经进入死循环，即存在负环。

时间复杂度：$\approx O(nm)$
空间复杂度：$O(n)$

SPFA 的时间复杂度自古以来便是众说纷纭，段凡丁在 1994 年的论文中证明 SPFA 算法时间复杂度为 $O(kn)$，其中 $k$ 是一个比较小的常数。但后来被指是伪证。之后更是出现了"SPFA 已死“的说法，原因是 SPFA 极容易被人为的数据卡住，退化为与 Bellman-Ford 相同的 $O(nm)$ 。所以 SPFA 还是慎用的好。

---

最短路例题

1.「USACO TRAINING」香甜的黄油(Floyd)

农夫 John 发现做出全威斯康辛州最甜的黄油的方法：糖。把糖放在一片牧场上，他知道 $n(1⩽n⩽500)$ 只奶牛会过来舔它，这样就能做出能卖好价钱的超甜黄油。当然，他将付出额外的费用在奶牛上。
农夫 John 很狡猾。像以前的巴甫洛夫，他知道他可以训练这些奶牛，让它们在听到铃声时去一个特定的牧场。他打算将糖放在那里然后下午发出铃声，以至他可以在晚上挤奶。
农夫 John 知道每只奶牛都在各自喜欢的牧场（一个牧场不一定只有一头牛）。给出各头牛在的牧场和牧场间的路线，找出使所有牛到达的路程和最短的牧场（他将把糖放在那）。

一句话题意：给定 $n$ 个点，试找出一个点使得其余各点到其距离之和最小。

数据范围告诉我们这题要用 Floyd。从 $1$ 到 $n$ 枚举牧场。同时，一个牧场里可能有不止 $1$ 与一条牛。所以可以用桶统计一个牧场中有多少头牛， 答案加上牛的数量乘上该牧场距离目标牧场的最短路长度。

...
int main() {
	scanf("%d%d%d", &n, &p, &c);
	SetUp();
	for(int i = 1; i <= n; i++) scanf("%d", &x), cnt[x]++; //cnt为桶
	for(int i = 1; i <= c; i++) {
		int u, v, w;
		scanf("%d%d%d", &u, &v, &w);
		dis[u][v] = dis[v][u] = w;
	}
	Floyd();
	for(int i = 1; i <= p; i++) {
		int tot = 0;
		for(int j = 1; j <= p; j++) tot += dis[i][j] * cnt[j];
		ans = min(tot, ans);
	}
	printf("%d", ans);
	return 0;
}

---

2.「NOI1997」最优乘车(Dijkstra)

H 城是一个旅游胜地，每年都有成千上万的人前来观光。为方便游客，巴士公司在各个旅游景点及宾馆，饭店等地都设置了巴士站并开通了一些单程巴士线路。每条单程巴士线路从某个巴士站出发，依次途经若干个巴士站，最终到达终点巴士站。
一名旅客最近到 H 城旅游，他很想去S公园游玩，但如果从他所在的饭店没有一路巴士可以直接到达 S 公园，则他可能要先乘某一路巴士坐几站，再下来换乘同一站台的另一路巴士, 这样换乘几次后到达 S 公园。
现在用整数 $1,2,\dots N$ 给 H 城的所有的巴士站编号，约定这名旅客所在饭店的巴士站编号为 1 ， S 公园巴士站的编号为 N 。
写一个程序，帮助这名旅客寻找一个最优乘车方案,使他在从饭店乘车到 S 公园的过程中换车的次数最少。

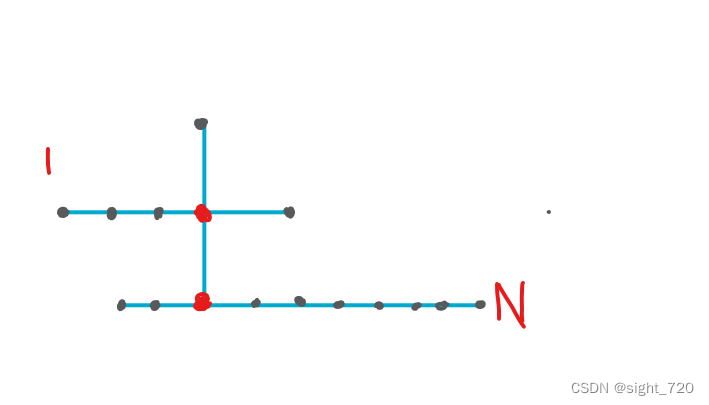
一个公交线路图可以抽象成上面这个样子。很明显在同一线路上的任意两点之间的边权为 $0$，即设有线路 $A$ 外一点 $P$，且 $P$ 所在线路与线路 $A$ 有交点，则该点到线路 $A$ 上交点的边权为 $1$，进而到达线路 $A$ 上任意一点边权皆为 $1$。

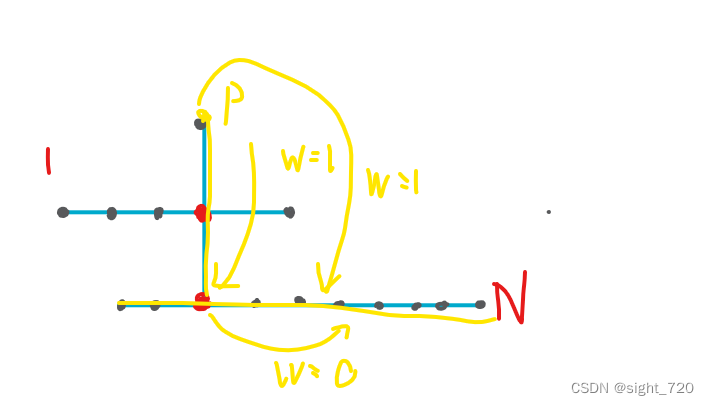
for(int i = 1; i <= m; i++) {
	int k = 0;
	char ch;
	while(~scanf("%d%c", &a[++k], &ch)) {
		if(ch != ' ') break;
	}
	for(int j = 1; j <= k; j++) {
		for(int l = j + 1; l <= k; l++) AddEdge(a[j], a[l], 1); //线路上任意两点对于线路外点来说边权为1
	}
}

最后用 Dijkstra 即可。

---

3.「CQOI2005」新年好(Dijkstra)

重庆城里有 $n$ 个车站， $m$ 条双向公路连接其中的某些车站。每两个车站最多用一条公路连接，从任何一个车站出发都可以经过一条或者多条公路到达其他车站，但不同的路径需要花费的时间可能不同。在一条路径上花费的时间等于路径上所有公路需要的时间之和。
佳佳的家在车站 $1$，他有五个亲戚，分别住在车站 $a,b,c,d,e$ 。过年了，他需要从自己的家出发，拜访每个亲戚（顺序任意），给他们送去节日的祝福。怎样走，才需要最少的时间？

第一大难点：最短路。

这道题应是多源最短路，但 $n$ 的最大值可以达到 $50000$ ，只能选用 Dijkstra 算法。如何用 Dijkstra 处理多源最短路？题目只要求了 $5$ 个源点，加上起点，一共有 $6$ 个，为常数，因此可以将多源最短路拆解成单源最短路。一次多源最短路等价于 $6$ 次单源最短路。定义 $di{s}_{i,j}$ 为以 $i$ 为起点到 $j$ 的最短路长度。

...
void Dijkstra(int s) {
	SetUp();
	dis[s][s] = 0; 
	pq.push(node(s, 0));
	...
}
...
for(int i = 1; i <= 5; i++) scanf("%d", &p[i]);
Dijkstra(1), Dijkstra(p[1]), Dijkstra(p[2]), Dijkstra(p[3]), Dijkstra(p[4]), Dijkstra(p[5]);

但由于 $s⩽n$ ，因此：

const int MAXN = 50000;
int dis[MAXN + 5][MAXN + 5];

优化：对于 $dis$ 数组的第一维，我们定义的是起点的标号。但我们已经将 $5$ 个起点存在了数组中，因此可以用数组的下标代替。重新定义 $di{s}_{i,j}$ 为 $p[i]$ 到 $j$ 的最短路长度。

...
void Dijkstra(int s) {
	SetUp();
	dis[s][p[s]] = 0; 
	pq.push(node(p[s], 0));
	...
}
...
for(int i = 1; i <= 5; i++) scanf("%d", &p[i]);
p[0] = 1;
Dijkstra(0), Dijkstra(1), Dijkstra(2), Dijkstra(3), Dijkstra(4), Dijkstra(5);

第二大难点，拜访顺序。

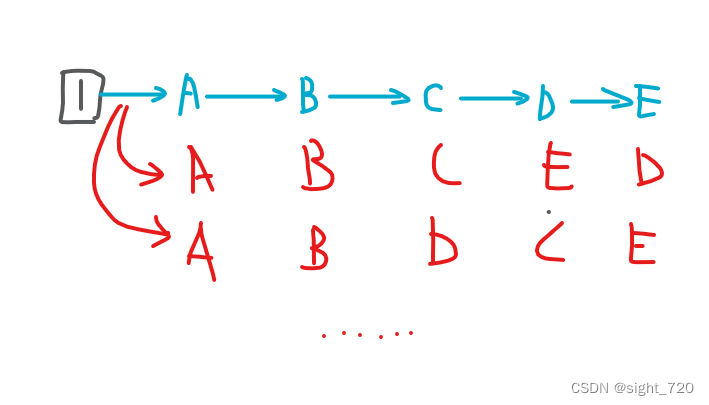
对于 $5$ 个节点总共可能的排列数为 $5!=120$ 种，只需要依次枚举顺序，按着顺序走，取最小值。（类似于全排列）

void dfs(int x, int cost, int step) { //x为已确定到第几个点，cost为目前的时间，step为选的下一个节点
	if(cost > ans) return; //剪枝
	if(x == 5) { //确定完了
		ans = min(ans, cost);
		return;
	}
	for(int i = 1; i <= 5; i++) {
		if(!vis[i]) {
			vis[i] = 1;
			dfs(x + 1, cost + dis[step][p[i]], i);
			vis[i] = 0;
		}
	}
}

---

4.「Vijos P1053」Easy SSSP(SPFA | Bellman-Ford)

输入数据给出一个有 $N$ 个节点，$M$ 条边的带权有向图。要求你写一个程序，判断这个有向图中是否存在负权回路。如果从一个点沿着某条路径出发，又回到了自己，而且所经过的边上的权和小于 $0$，就说这条路是一个负权回路。
如果存在负权回路，只输出一行 $-1$；如果不存在负权回路，再求出一个点 $S$ 到每个点的最短路的长度。约定：$S$ 到 $S$ 的距离为 $0$，如果 $S$ 与这个点不连通，则输出 NoPath。

能判负环的算法只有 Bellman-Ford 和 SPFA ，所以这道题两种算法皆可。很容易想到从 $S$ 开始遍历图，如果有负环就跳出，否则依次输出各点到 $S$ 的距离。

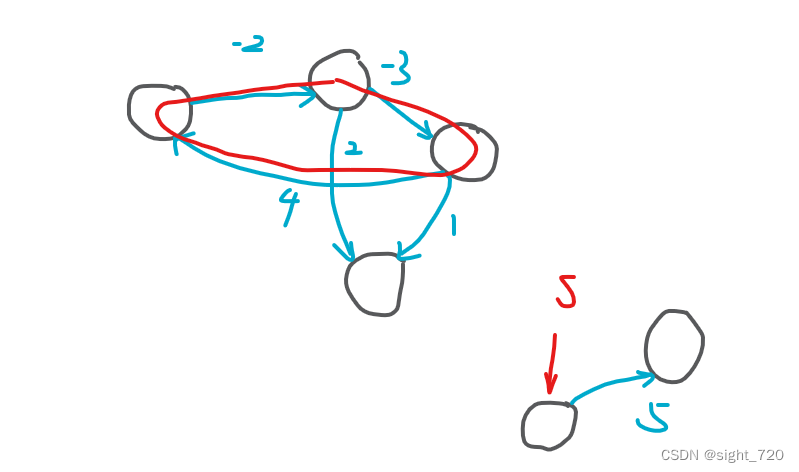
上图中展现了一种特殊情况——当图为非联通图时，SPFA 从 $S$ 开始，却不能遍历整张图，即使图中存在负环（上图红圈部分），SPFA 也没办法判断。

既然存在不连通的情况，我们就可以让 SPFA 从每一个点开始遍历，从而遍历整张图，存在负环就输出并结束程序，否则最后 SPFA 再从 $S$ 开始求出每一个点到 $S$ 的距离。

void SetUp() {
	for(int i = 0; i <= ...; i++) dis[i] = inf;
	for(int i = 0; i <= ...; i++) vis[i] = 0;
	for(int i = 0; i <= ...; i++) cnt[i] = 0; 
}
int SPFA(int bg) {
	SetUp();
	queue<int> q;
	dis[bg] = 0, vis[bg] = 1, cnt[bg] = 1;
	q.push(bg);
	while(!q.empty()) {
		int u = q.front();
		q.pop();
		vis[u] = 0;
		for(int i = Head[u]; i; i = Next[i]) {
			int v = Vertex[i];
			int w = Edge[i];
			if(dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				if(!vis[v]) {
					q.push(v);
					mark[v] = 1; //mark数组为标记，标记是否被遍历
					vis[v] = 1;
					cnt[v]++;
					if(cnt[v] >= n) {
						printf("-1");
						exit(0);
					} 
				}
			}
		}
	}
  	return 0;
}
...
for(int i = 1; i <= n; i++) {
	if(!mark[i]) { //没被遍历就以其为起点
		SPFA(i);
	}
}
SPFA(s); 
for(int i = 1; i <= n; i++) {
	if(dis[i] == inf) printf("NoPath\n");
	else printf("%lld\n", dis[i]);
}

---

#4 图论 | 最小生成树

$n$ 个点用 $n-1$ 条边连接起来形成的联通块只能是树，反过来说，一棵拥有 $n$ 个节点的树只有 $n-1$ 条边。在一张有 $n$ 个节点的图中用 $n-1$ 条边连接起来的联通块叫做 生成树。

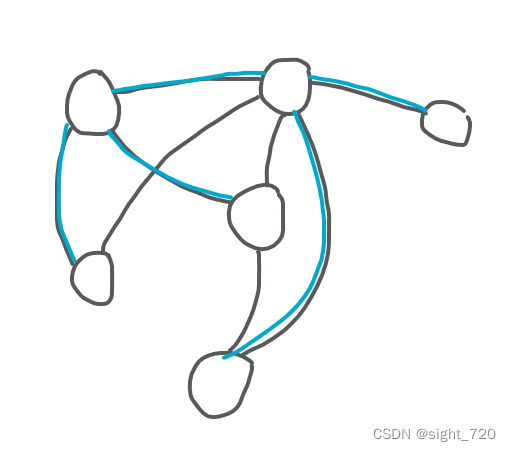
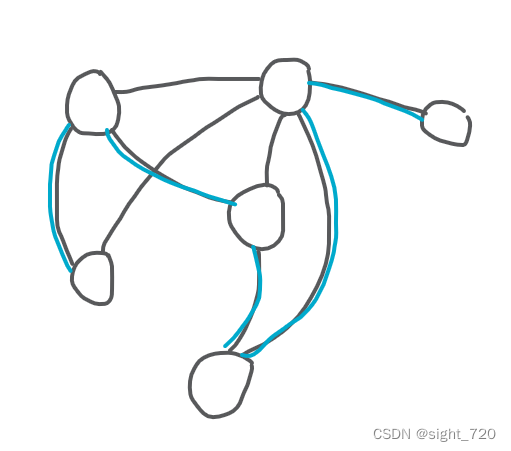
一张图中可能存在多棵生成树。在这些生成树中，边权和最小的生成树被称为 最小生成树。

1.Prim 算法

由 Vojtěch Jarník 发现，以 Robert C. Prim 命名。本质上是贪心。

实现方法和 Dijkstra 如出一辙。以任意一点为基准点（常以 $1$ 为基准点），将节点分成蓝白两个阵营。蓝阵营包含已经确定与最小生成树相连的点，白阵营则包含未确定的。不断地从白阵营中取出距离蓝阵营（目前构建的最小生成树）最近（边权最小）的店加入蓝阵营，然后总的边权和加上该边权。

#define inf 0x3f3f3f3f
void SetUp() {
	for(int i = 0; i <= ...; i++) dis[i] = inf;
	for(int i = 0; i <= ...; i++) vis[i] = 0;
}
int Prim() {
	int MST = 0;
	SetUp();
	d[1] = 0; //d[v]表示蓝点v与白点相连的最小边权
	for(int i = 1; i < n; i++) {
		int x = 0;
		for(int j = 1; j <= n; j++) { //找最近的白点
			if(!vis[j] && (x == 0 || d[j] < d[x]) x = j;
		}
		vis[x] = 1;
		for(int j = 1; j <= n; j++) {
			if(!vis[j] && d[j] > G[x][j]) d[j] = G[x][j]; //将白点变蓝后周围的点也要变（可能离蓝阵营更近了）
		}
		MTS += d[x];
	}
	return MST;
}

时间复杂度：$O(n^2)$
空间复杂度：$O(n)$

优点：在处理稠密图时跑的飞快；可以去重边。
缺点：平均时间复杂度较高。

---

2.堆优化 Prim 算法

可以看到 Prim 算法像极了 Dijkstra，这也让我们产生了优化的欲望。

大循环内的第一个循环的作用是找 $d$ 数组里的最小值，可以用堆进行优化，从 $O(n)$ 降到 $O(\log n)$；第二重循环用的是邻接矩阵，可以用邻接表或者链式前向星优化。

struct node {
	int u, w;
	node(int _u, int _w) { u = _u, w = _w; }
	friend bool operator<(node x, node y) { return x.w > y.w; }
};
priority_queue<node> pq;
...
void SetUp() {
	for(int i = 0; i <= ...; i++) d[i] = inf;
	for(int i = 0; i <= ...; i++) vis[i] = 0;
}
int Prim() {
	int MST = 0;
	SetUp();
	d[1] = 0;
	pq.push(node(1, 0));
	while(!pq.empty()) {
		int u = pq.top().u;
		pq.pop();
		if(vis[u]) continue;
		vis[u] = 1;
		for(int i = Head[u]; i; i = Next[i]) { //链式前向星
			int v = Vertex[i];
			int w = Edge[i];
			if(!vis[v] && d[v] > w) {
				d[v] = w;
				pq.push(node(v, d[v]));
			}
		}
		MST += d[u];
	}
	return MST;
}

越来越像 Dijkstra 了。

时间复杂度：$\approx O(m\log n)$
空间复杂度：$O(n)$

优点：平均时间复杂度低；可去重边。
缺点：处理稠密图时慢。

---

3.Kruskal 算法

由 Joseph B. Kruskal 于 1956 年发表。本质上是贪心。

Kruskal 算法运用了并查集的思想，起初每个点各自构成一个集合，所有边按照边权从小到大排序，依次扫描，若当前扫描到的边不在同一集合就合并。与 Prim 算法相比，Kruskal 算法没有基准点，该算法是不断选择两个距离最近的集合进行合并的过程。

void MakeSet() { for(int i = 1; i <= n; i++) father[i] = i; }
int FindSet(int x) {
	if(father[x] == x) return x;
	else return father[x] = FindSet(father[x]);
}
int Kruskal() {
	MakeSet();
	int cnt = 0, MST = 0;
	sort(s + 1, s + m + 1, cmp);
	for(int i = 1; i <= m; i++) {
		int fx = FindSet(s[i].u), fy = FindSet(s[i].v);
		if(fx == fy) continue;
		father[fx] = fy;
		MST += s[i].w;
		cnt++;
		if(cnt == n - 1) return MST; //n-1一条边连接n个节点组成的联通块就是一棵树
	}
	return MST;
}

时间复杂度：$\approx O(m\log m)$
空间复杂度：$O(n)$

优点：平均时间复杂度低；处理稀疏图时跑的飞快。
缺点：不可去重边；处理稠密图时慢。

---

最小生成树例题

1.「AcWing346」走廊泼水节(Kruskal)

给定一棵 $N$ 个节点的树，要求增加若干条边，把这棵树扩充为完全图，并满足图的唯一最小生成树仍然是这棵树。
求增加的边的权值总和最小是多少。

完全图的定义：每对不同的顶点之间都恰连有一条边相连的图。

要想把一棵树扩充成一张完全图，只需要在 Kruskal 合并时将两个集合间添加若干条边使得合并后的图为完全图。这样从小到大层层合并，最终合并完成后一定可以保证为完全图。

现在有这么一张图：

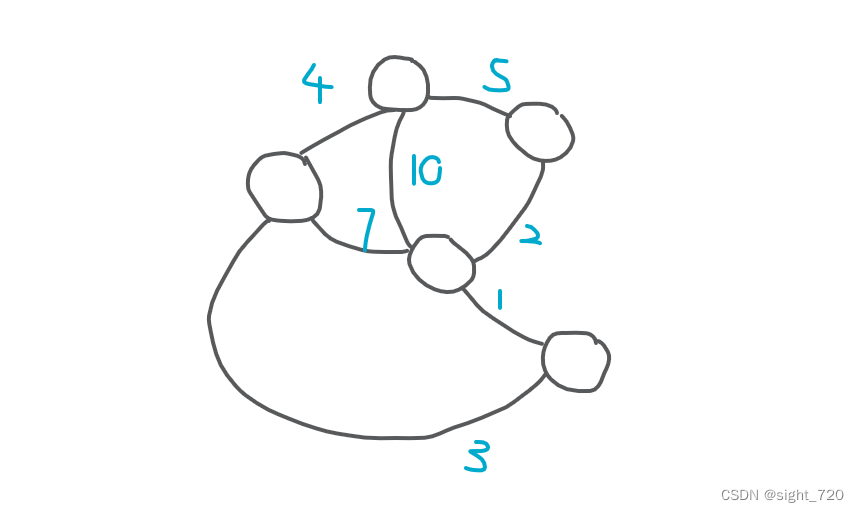
第一次合并：

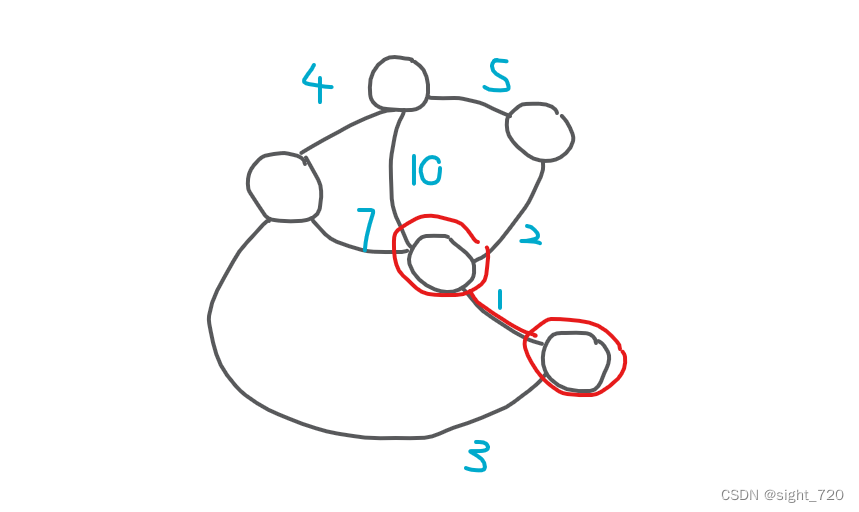
两个点要构成完全图需要连 $1$ 根边，这里已经存在一条边，故花费不增加。

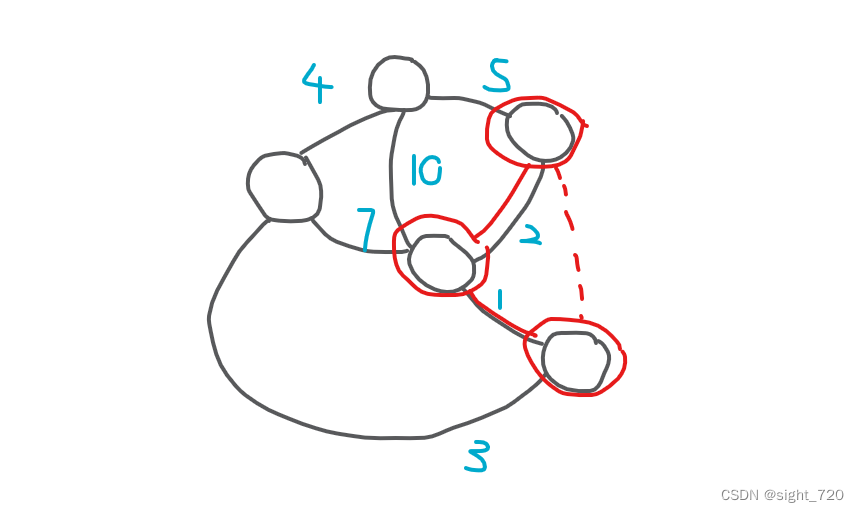
三个点需要 $3$ 条边，这里少了一条，需要额外花费添加一条边。又因为要保证在合并后最小生成树不变，因此添加的边权值需要大于原边，即在上图中需要找到一个比 $2$ 大的尽可能小的整数，即 $3$ ，所以花费增加 $3$ 。

…

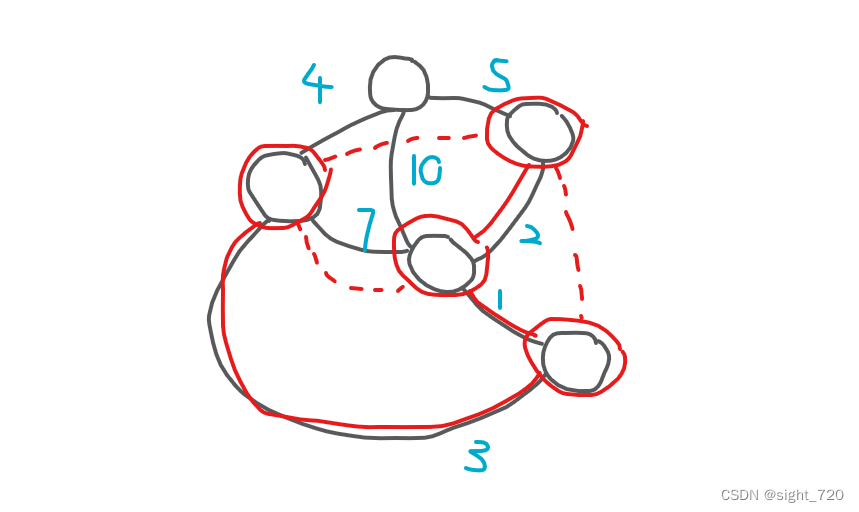
在合并过程中，会发现一个规律：

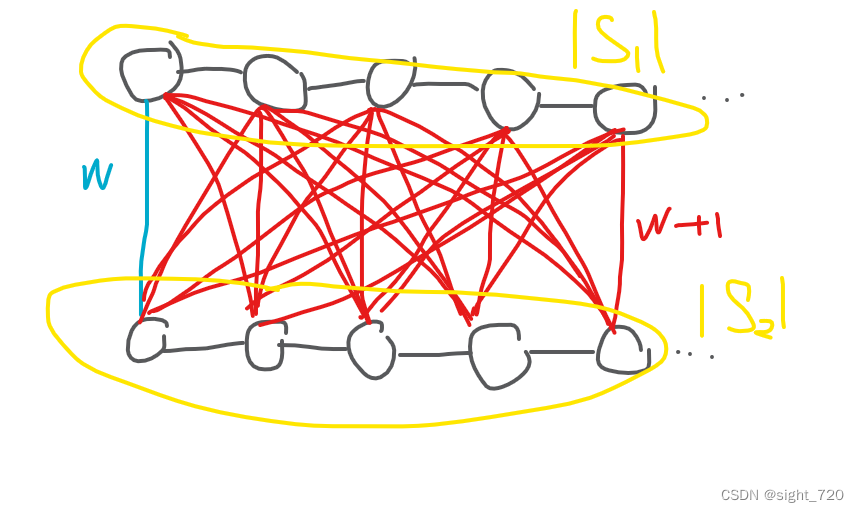
每次合并时增加的花费为：

$$(w_{i,j}+1)(|S_1||S_2|-1)$$

对于两个元素数分别为 $|S_1|$ 和 $|S_2|$ 的集合，他们想要构成完全图需要连 $|S_1||S_2|$ 条边。又因为已经存在了一条边权为 $w_{i.j}$ 的边，所以还要连 $|S_1||S_2|-1$ 条。对于每一条新加的边，为了让总花费最小且合并后最小生成树不变，边权应设为 $w_{i,j}+1$，就有了上面的式子。

void MakeSet() {
	for(int i = 0; i <= MAXN; i++) father[i] = i, size[i] = 1; //size为集合大小
}
int FindSet(int x) {
	if(father[x] == x) return x;
	else return father[x] = FindSet(father[x]);
}
int Kruskal() {
	MakeSet();
	int MST = 0;
	sort(s + 1, s + n, cmp);
	for(int i = 1; i < n; i++) {
		int fx = FindSet(s[i].u), fy = FindSet(s[i].v);
		if(fx == fy) continue;
		MST += (s[i].w + 1) * (size[fx] * size[fy] - 1); //公式
		father[fx] = fy;
		size[fy] += size[fx];
	}
	return MST;
}

---

2.新的开始(Kruskal)

发展采矿业当然首先得有矿井，小 FF 花了上次探险获得的千分之一的财富请人在岛上挖了 $n$ 口矿井，但他似乎忘记考虑的矿井供电问题……
为了保证电力的供应，小 FF 想到了两种办法：
在这一口矿井上建立一个发电站，费用为 $v$（发电站的输出功率可以供给任意多个矿井）。
将这口矿井与另外的已经有电力供应的矿井之间建立电网，费用为 $p$ 。
小 FF 希望身为「NewBe_One」计划首席工程师的你帮他想出一个保证所有矿井电力供应的最小花费。

对于电网的铺设，运用最小生成树不难想到。但对于发电站的建设有些棘手。不妨把发电站也看作一条边。

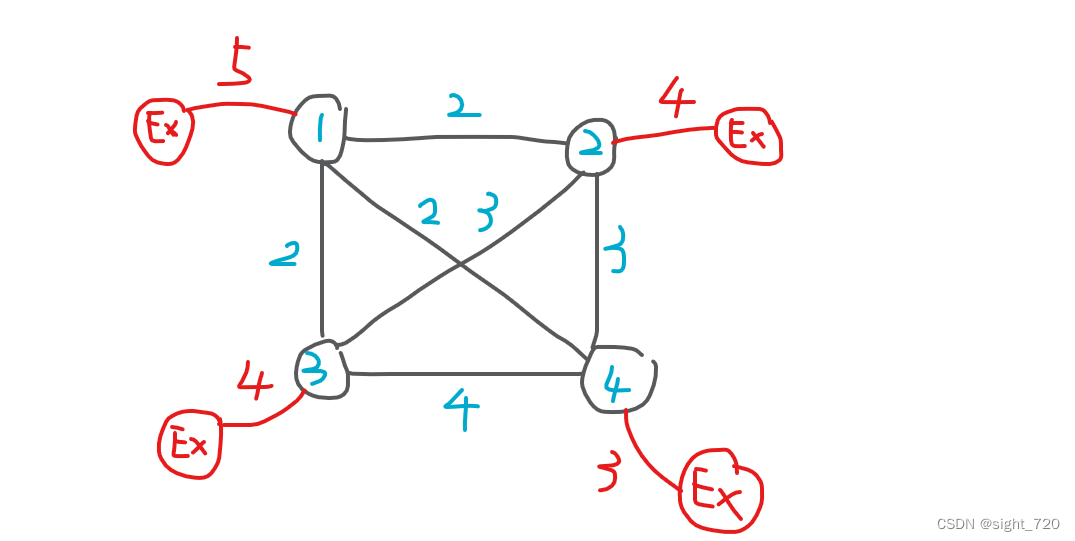
似乎打开了思路。是不是就这样处理后用 Kruskal 处理就行了？并不是。考虑一种特殊情况：

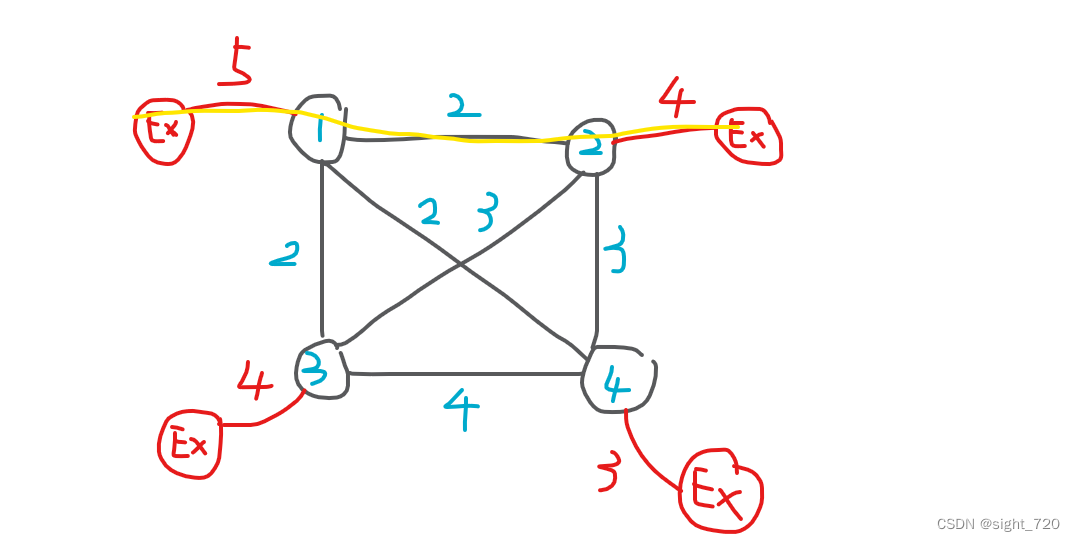
Kruskal 将黄色部分纳入了最小生成树，这代表着在 $1$、$2$ 号节点上分别建发电站，之后还要在两点间铺电网，岂不是多余？

上面我们将 $n$ 个节点连接上 $n$ 个节点，似乎将 $n$ 个节点连在一个节点上又是别有洞天。

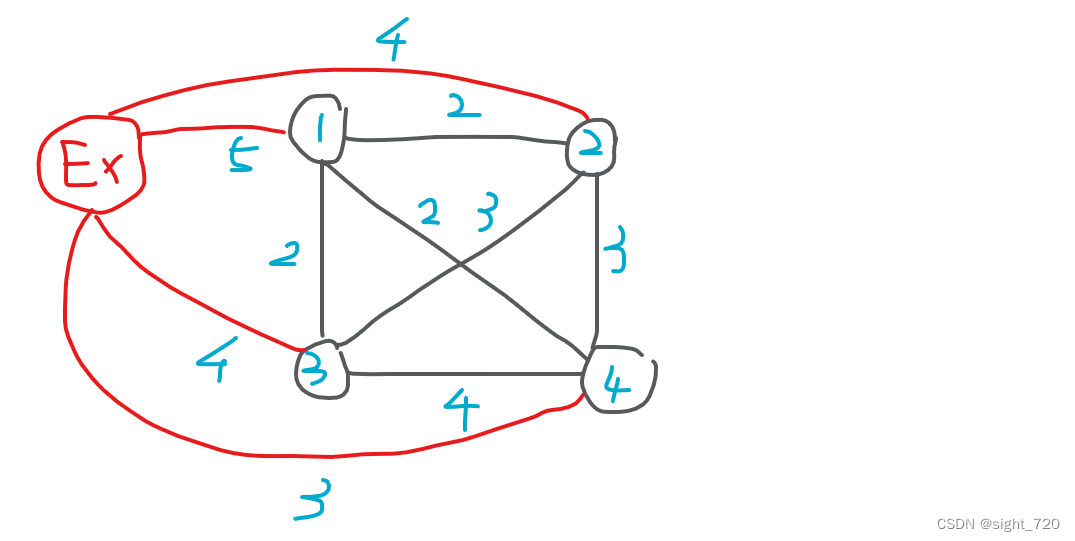
会发现这样一连后问题便迎刃而解。因为连接在同一个节点上后，$n$ 个节点实则处在同一集合，不存在互相之间多余连接的情况。

...//Kruskal部分省略
for(int i = 1; i <= n; i++) {
	scanf("%d", &p[i]);
	tot++;
	s[tot].u = i, s[tot].v = 0, s[tot].w = p[i];
}
for(int i = 1; i <= n; i++) {
	for(int j = 1; j <= n; j++) {
		int x;
		scanf("%d", &x);
		if(i == j) continue;
		tot++;
		s[tot].u = i, s[tot].v = j, s[tot].w = x;
	}
}

---

3.「BZOJ4883 Lydsy1705月赛」棋盘上的守卫(Kruskal)

在一个 $n\ast m$ 的棋盘上要放置若干个守卫。对于 $n$ 行来说，每行必须恰好放置一个横向守卫；同理对于 $m$ 列来说，每列必须恰好放置一个纵向守卫。
每个位置放置守卫的代价是不一样的，且每个位置最多只能放置一个守卫，一个守卫不能同时兼顾行列的防御。请计算控制整个棋盘的最小代价。

对于一个点 $P$，坐标为 $(i,j)$，如果直接用 $i,j,w_{i,j}$ 进行存边会导致在某些情况下 $i$ 会等于 $j$，出现紊乱。这不利于最小生成树的计算。因而我们用 $i,j+n,w_{i,j}$ 进行存边，根据是 max ⁡ { i } = n \max\{i\}=n max{i}=n，从而避免了该情况。

假设我们有一个 $n\ast m$ 的矩阵。先将矩阵的第一行存下，将其归入一个集合：

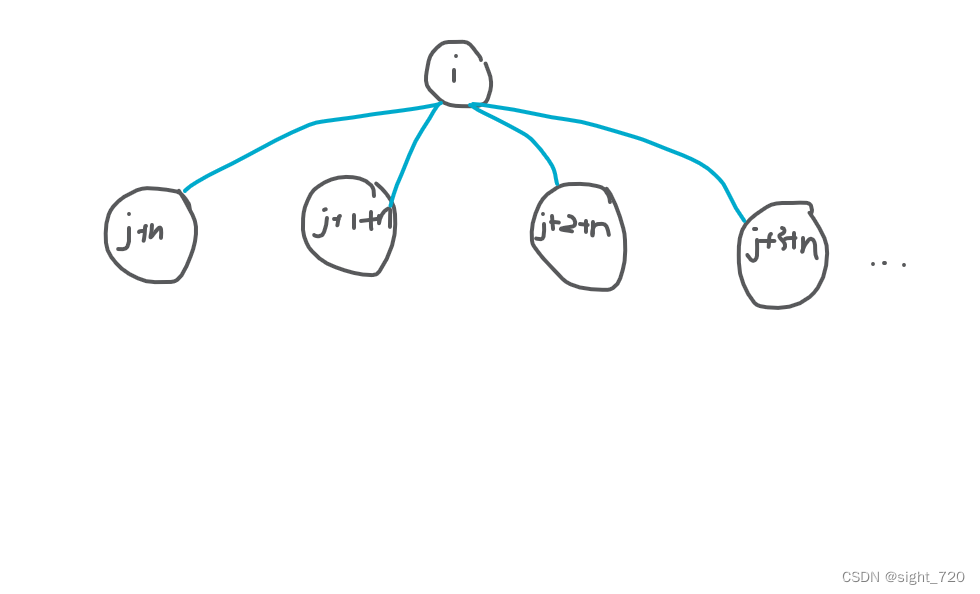
此时这是一棵树。根节点是一个横向的守卫，守护着这一行。但是对于每一个节点所在的列却无人守护。不慌，再加入第二行：

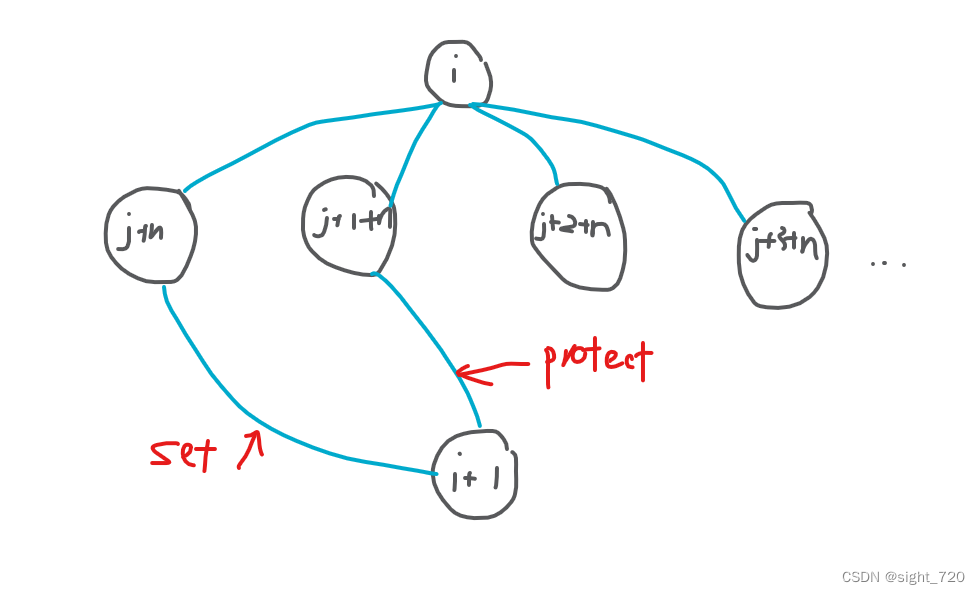
这时多来的一个点是纵向的守卫，只能守护一列。这里有 $m$ 列需要守护，这个点需要放在一列上，而他自己也要守护一列，与原来的树连接后就成了上图的样子。此时的树不再是树，而是一棵 基环树（有且只有一个环的连通图）。这道题就是要维护一棵基环树，只能有一个环。此时定义一个数组 $mark$，标记节点所在的树是否是基环树。在 Kruskal 合并时，如果两个节点所在的树为基环树，则不能累加边权，跳过，否则继续操作，如果两点在同一集合有要连接，说明产生了环，将节点所在并查集的代表标记为 $1$，否则按正常的 Kruskal 合并。

...
for(int i = 1; i <= tot; i++) {
	int fx = FindSet(s[i].u), fy = FindSet(s[i].v);
	if(vis[fx] && vis[fy]) continue; //双方都是基环树
	else if(fx == fy) { //在同一集合
		vis[fx] = 1; //树内自己连自己，形成环
		MST += s[i].w;
	}
	else {
		father[fx] = fy;
		vis[fy] or_eq vis[fx]; //只要双方有一个所在的树上有环，合并后就有环
		MST += s[i].w;
	}
}

---

（未完）