关于『 一月の集训 』
A B O U T J A N U A R Y \tt A \ B \ O \ U \ T \quad J \ A\ N\ U\ A\ R \ Y A B O U TJ A N U A R Y
关于一月的集训,在这里做一个了结总结。
名称:一月集训
承办方:重庆市第八中学
时间: J A N . 23 → J A N . 28 \tt JAN.23 \to JAN.28 JAN.23→JAN.28
很乱是吧,同感。
1.分治
D I V I D E A N D C O N Q U E R \tt \ \ \ D \ I \ V \ I \ D \ E \quad \ A \ N \ D \quad C \ O \ N \ Q \ U \ E \ R D I V I D E A N DC O N Q U E R
“分治,字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。”
− \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - −摘自百度百科
综上,分治的基本思想为:
分治的步骤:
-
例题:
-
- 快速排序 ( Q u i c k l y _ s o r t \tt Quickly\_sort Quickly_sort)
-
- 二路归并排序 ( M e r g e _ s o r t \tt Merge\_sort Merge_sort)
-
- 求逆序对数 ( R e v e r s e _ o r d e r _ p a i r \tt Reverse\_order\_pair Reverse_order_pair)
-
- 寻找伪币 ( C o u n t e r f e i t _ c u r r e n c y \tt Counterfeit\_currency Counterfeit_currency)
-
- 查找最接近的元素
-
- 一元三次方程求解
-
- 网线主管
-
- 膨胀的木棍 ( S t i c k \tt Stick Stick)
快速排序 & 二路归并排序
| 快速排序 | 二路归并排序 |
|---|---|
| 不稳定排序 | 稳定排序 |
| 双指针 & 二分 | 二分 |
快速排序:
void quickly_sort(int s, int e) {
if(s > e) {
return;
}
int tmp = a[s];
int i = s;
int j = e;
while(i != j) {
while(a[j] <= tmp && i < j) {
j --;
}
while(a[i] >= tmp && i < j) {
i ++;
}
if(i < j) {
swap(a[i], a[j]);
}
}
swap(a[i], a[s]);
quickly_sort(s, i - 1);
quivkly_sort(i + 1, e);
return;
}
二路归并:
void merge_sort(int s, int e) {
if(s == e) {
return;
}
int mid = (s + e) / 2;
merge_sort(s, mid);
merge_sort(mid + 1, e);
int i = s;
int k = s;
int j = mid + 1;
while(i <= mid && j <= e) {
if(a[i] <= a[j]) {
r[k] = a[i];
k ++;
i ++;
}
else {
r[k] = a[j];
k ++;
j ++;
}
}
while(i <= mid) {
r[k] = a[i];
i ++;
k ++;
}
while(j <= e) {
r[k] = a[j];
j ++;
k ++;
}
for(int i = s; i <= e; i ++) {
a[i] = r[i];
}
return;
}
时间复杂度为 O ( n log n ) \tt O(n\log n) O(nlogn)。
求逆序对
“逆序对,数学术语,设 A \tt A A 为一个有 n \tt n n 个数字的有序集 ( n > 1 \tt n > 1 n>1),其中所有数字各不相同。
如果存在正整数 i \tt i i, j \tt j j 使得 1 ≤ i < j ≤ n \tt1 \leq i < j \leq n 1≤i<j≤n 而且 A [ i ] > A [ j ] \tt A[i] > A[j] A[i]>A[j],则 < A [ i ] , A [ j ] > \tt <A[i], A[j]> <A[i],A[j]> 这个有序对称为 A \tt A A 的一个逆序对,也称作逆序数。”
− \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - −摘自百度百科
看起来求逆序对又是大费周章,但其实在二路归并排序时,有一段代码:
else {
r[k] = a[j];
k ++;
j ++;
}
先看 e l s e \tt else else 否定的是前面的 a [ i ] < = a [ j ] \tt a[i] <= a[j] a[i]<=a[j] , 则:
if(a[i] > a[j]) {
r[k] = a[j];
k ++;
j ++;
}
再看 w h i l e \tt while while 里写的是 i < = m i d & & j < = e \tt i <= mid \ \&\& \ j <= e i<=mid && j<=e , 又因为 m i d = s + e 2 \tt mid = \frac {s + e}{2} mid=2s+e , s < e \tt s < e s<e, 则 m i d < e \tt mid < e mid<e , 则 i < j \tt i < j i<j 。
满足逆序对的定义。
又想,既然 a [ i ] > a [ j ] \tt a[i] > a[j] a[i]>a[j], 则 a [ j ] \tt a[j] a[j]后的所有数均可和其互为逆序对。
则有:
else {
r[k] = a[j];
k ++;
j ++;
ans += mid - i + 1;//求逆序对
}
但不能用快速排序求逆序对。
快速排序为不稳定排序,会导致相等元素下标交换。
寻找伪币
给你一个装有 16 \tt 16 16 枚硬币的袋子。 16 \tt 16 16 枚硬币中有一个是伪造的,并且那个伪造的硬币比真的硬币要轻一些。你的任务是找出这枚伪造的硬币。为了帮助你完成这一任务,将提供一台可用来比较两组硬币重量的仪器,比如天平。利用这台仪器,可以知道两组硬币的重量是否相同。
二分裸题。
想象一把天平,称重时伪币一定在轻的那一边。
则确定二分左指针 l = 1 \tt l = 1 l=1, 右指针 r = 16 \tt r = 16 r=16。
令 m i d = s + e 2 \tt mid = \frac {s + e}{2} mid=2s+e 。
则当 ∑ i = l m i d a i < ∑ i = m i d + 1 r a i \tt \sum_{i = l}^{mid}a_i < \sum_{i = mid + 1}^{r}a_i i=l∑midai<i=mid+1∑rai 时,伪币在 [ l , m i d ] \tt [l, mid] [l,mid] 中。
反之,伪币在 [ m i d + 1 , r ] \tt [mid + 1, r] [mid+1,r] 中。
为了降低时间复杂度,故采用前缀和 ( P r e a f i x s u m ) \tt (Preafix \ sum) (Preafix sum) 数组。
int main() {
for(int i = 1; i <= 16; i ++) {
scanf("%d", &a[i]);
prev[i] = prev[i - 1] + a[i];
}
int l = 1;
int r = 16;
while(l < r) {
int mid = (l + r) /2;
int suml = prev[mid] - prev[l - 1];
int sumr = prev[r] - prev[mid];
if(suml < sumr) {
r = mid;
}
else {
l = mid + 1;
}
}
printf("%d %d", l, a[l]);
return 0;
}
查找最接近的元素
在一个非降序列中,查找与给定值最接近的元素。
普通的二分查找。
值得注意的是:
查找与给定值最接近的元素。
所以在 w h i l e \tt while while 循环后, 还要进行一次判断:
if(x - a[l] <= a[r] - x) {//x是询问的数(查找对象)
printf("%d\n", a[l]);
}
什么意思?
当 ∣ a [ l ] − x ∣ < ∣ a [ r ] − x ∣ \tt | a[l] - x | < | a[r] - x | ∣a[l]−x∣<∣a[r]−x∣ 时, 输出 a [ l ] \tt a[l] a[l] 。
否则输出 a [ r ] \tt a[r] a[r] 。
一元三次方程求解
有形如: a x 3 + b x 2 + c x + d = 0 \tt ax^3+bx^2+cx+d=0 ax3+bx2+cx+d=0 这样的一个一元三次方程。给出该方程中各项的系数( a , b , c , d \tt a,b,c,d a,b,c,d 均为实数),并约定该方程存在三个不同实根(根的范围在 − 100 \tt -100 −100 至 100 \tt 100 100 之间),且根与根之差的绝对值 ≥ 1 \tt \geq 1 ≥1。 要求由小到大依次在同一行输出这三个实根(根与根之间留有空格),并精确到小数点后2位。
N O I P 2001 \tt NOIP \ 2001 NOIP 2001 提高组。
这种二分非直接分出答案,而是通过某些运算间接分出答案。
而我们往往将这某种运算写成函数,取名为 c h e c k \tt check check 。
int check(int x)
回到这道题。
首先导入一个概念:
零点定理
如果函数 y = f ( x ) \tt y= f(x) y=f(x)在区间 [ a , b ] \tt [a,b] [a,b]上的图象是连续不断的一条曲线,并且有 f ( a ) × f ( b ) < 0 \tt f(a) \times f(b)<0 f(a)×f(b)<0 , 那么,函数 y = f ( x ) \tt y= f(x) y=f(x) 在区间 ( a , b ) \tt (a,b) (a,b) 内有零点,即至少存在一个 c ∈ ( a , b ) \tt c\in (a,b) c∈(a,b),使得 f ( c ) = 0 \tt f(c)=0 f(c)=0 , 这个 c \tt c c 也就是方程 f ( x ) = 0 \tt f(x)= 0 f(x)=0 的根。
− \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - −摘自百度百科
这就好办了。
double check(double x) {
return x * x * x * a + b * x * x + c * x + d;
}
int main() {
scanf("%lf %lf %lf %lf", &a, &b, &c, &d);
for(double x = -100; x < 100; x += 1.0) {
l = x;
r = x + 1;
if(check(l) == 0) {
printf("%.2lf ", l);
}
else if(check(l) * check(r) < 0) {
while(r - l > 0.0001) {
mid = (r + l) / 2;
if((check(l) * check(mid)) < 0) {
r = mid;
}
else l = mid;
}
printf("%.2lf ", l);
}
}
return 0;
}
网线主管
仙境的居民们决定举办一场程序设计区域赛。裁判委员会完全由自愿组成,他们承诺要组织一次史上最公正的比赛。他们决定将选手的电脑用星形拓扑结构连接在一起,即将它们全部连到一个单一的中心服务器。为了组织这个完全公正的比赛,裁判委员会主席提出要将所有选手的电脑等距离地围绕在服务器周围放置。
为购买网线,裁判委员会联系了当地的一个网络解决方案提供商,要求能够提供一定数量的等长网线。裁判委员会希望网线越长越好,这样选手们之间的距离可以尽可能远一些。
该公司的网线主管承接了这个任务。他知道库存中每条网线的长度(精确到厘米),并且只要告诉他所需的网线长度(精确到厘米),他都能够完成对网线的切割工作。但是,这次,所需的网线长度并不知道,这让网线主管不知所措。
你需要编写一个程序,帮助网线主管确定一个最长的网线长度,并且按此长度对库存中的网线进行切割,能够得到指定数量的网线。
题目很长, 简单说就是:
有若干条线段,求能使线段切割后总数一定的最大单位。
仍然是间接二分。
则首先确定 c h e c k \tt check check 函数的内容。
二分分出来的是单位长度,而要与线段数量相比,很明显, 用一层 f o r \tt for for 循环累加每条线段按单位长度分得的线段数量。
int check(int x) {
int ans = 0;
for(int i = 1; i <= n; i ++) {
ans += a[i] / x;
}
return ans;
}
注意:为避免精度问题,将 d o u b l e \tt double double 转化为 i n t \tt int int 后处理,输出时将 i n t \tt int int 还原回 d o u b l e \tt double double 即可。
膨胀的木棍
当一根细木棍被嵌在两堵墙之间被加热,它将膨胀形成弓形的弧,而这个弓形的弦恰好是未加热前木棍的原始位置。
你的任务是计算木棍中心的偏移距离。
热力学 & 三角学 & 高等数学联袂出演。

前方高能。
先热个身:
线性膨胀系数
固体物质的温度每改变1摄氏度时,其长度的变化和它在原温度(不一定为 0 ℃ \tt 0℃ 0℃ )时长度之比,叫做“线性膨胀系数"。单位为 ℃ − 1 \tt ℃^{-1} ℃−1。符号为 α t \tt αt αt。其定义式是 α t = L t − L 0 L 0 \tt αt=\frac{L_t-L_0}{L_0} αt=L0Lt−L0 ,即有, L t = L 0 ( 1 + α t \tt L_t=L_0(1+αt Lt=L0(1+αt)。
− \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - −摘自百度百科
∵ l t = l 0 ( 1 + α t ) \tt l_t = l_0( 1 + \alpha t) lt=l0(1+αt)
又∵ ∠ α = arcsin ( l r ) \tt ∠\alpha = \arcsin(\frac{l}{r}) ∠α=arcsin(rl)
∴ ( 1 + α t ) l = 2 r × arcsin ( l 2 r ) \tt (1 + \alpha t)l = 2r \times \arcsin(\frac{l}{2r}) (1+αt)l=2r×arcsin(2rl)
∵ r = k 2 + l 2 \tt r = \sqrt{k^2 + l^2} r=k2+l2
又∵ d = r − k \tt d = r - k d=r−k
∴ d = k 2 + l 2 − k \tt d = \sqrt{k^2 + l^2} - k d=k2+l2−k
… \dots …
最终得
r = h 2 + l 2 8 h \tt r = \frac{h}{2} + \frac{l^2}{8h} r=2h+8hl2
设弧长 x \tt x x。
则
x = ( 2 h + l 2 2 h ) × arcsin ( 2 h 4 h 2 + l 2 ) \tt x = (2h + \frac{l^2}{2h}) \times \arcsin(\frac{2h}{4h^2+l^2}) x=(2h+2hl2)×arcsin(4h2+l22h)
对上式求导得
x ′ = ( ( 2 h + l 2 2 h ) × arcsin ( 2 h 4 h 2 + l 2 ) ) ′ \tt x\prime = ((2h + \frac{l^2}{2h}) \times \arcsin(\frac{2h}{4h^2+l^2}))\prime x′=((2h+2hl2)×arcsin(4h2+l22h))′
由求导四则运算法则与性质得
( u ( x ) × v ( x ) ) ′ = u ′ ( x ) × v ( x ) + u ( x ) × v ′ ( x ) \tt (u(x) \times v(x))\prime = u\prime(x) \times v(x) + u(x) \times v\prime(x) (u(x)×v(x))′=u′(x)×v(x)+u(x)×v′(x)
( u ( x ) ± v ( x ) ) ′ = u ′ ( x ) + v ′ ( x ) \tt (u(x)±v(x))\prime = u\prime(x) + v\prime(x) (u(x)±v(x))′=u′(x)+v′(x)
(
u
(
x
)
v
(
x
)
)
′
=
u
′
(
x
)
v
(
x
)
−
u
(
x
)
v
′
(
x
)
v
2
(
x
)
\tt (\frac{u(x)}{v(x)})\prime = \frac{u\prime(x)v(x) - u(x)v\prime(x)}{v^2(x)}
(v(x)u(x))′=v2(x)u′(x)v(x)−u(x)v′(x)
则
( ( 2 h + l 2 2 h ) × arcsin ( 2 h 4 h 2 + l 2 ) ) ′ = ( 2 h + l 2 2 h ) ′ × arcsin ( 2 h 4 h 2 + l 2 ) + ( 2 h + l 2 2 h ) × arcsin ( 2 h 4 h 2 + l 2 ) ′ \tt ((2h + \frac{l^2}{2h}) \times \arcsin(\frac{2h}{4h^2+l^2}))\prime = (2h + \frac{l^2}{2h})\prime \times \arcsin(\frac{2h}{4h^2+l^2}) + (2h + \frac{l^2}{2h})\times \arcsin(\frac{2h}{4h^2+l^2})\prime ((2h+2hl2)×arcsin(4h2+l22h))′=(2h+2hl2)′×arcsin(4h2+l22h)+(2h+2hl2)×arcsin(4h2+l22h)′
化简得
x ′ = 4 h + 2 h l + l 2 2 h × arcsin ( 2 h 4 h 2 + l 2 ) + 4 h 2 + l 2 2 h 1 − 16 h 4 − 8 h 2 l 2 − l 4 \tt x\prime = \frac{4h + 2hl + l^2}{2h} \times \arcsin(\frac{2h}{4h^2 + l^2}) + \frac{4h^2+l^2}{2h\sqrt{1 - 16h^4 - 8h^2l^2 - l^4}} x′=2h4h+2hl+l2×arcsin(4h2+l22h)+2h1−16h4−8h2l2−l44h2+l2
∴ x \tt x x 单调递增。
注意:二分时精度需开大。
int main() {
double len, n, c;
while(scanf("%lf%lf%lf", &len, &n, &c)) {
if (len == -1 && n == -1 && c == -1) {
return 0;
}
double l = 0.0;
double r = 0.5 * len;
double mid;
double l1 = (1 + n * c) * len;
while(r - l > 0.00001) {
mid = (l + r) / 2;
r = (4 * mid * mid + len * len) / (8 * mid);
if (2 * r * asin(len / (2 * r)) < l1) {
l = mid;
}
else {
r = mid;
}
}
printf("%.3lf\n", mid);
}
}
2.STL之队列
Q U E U E \tt \ \ \ Q \ U \ E\ U \ E Q U E U E
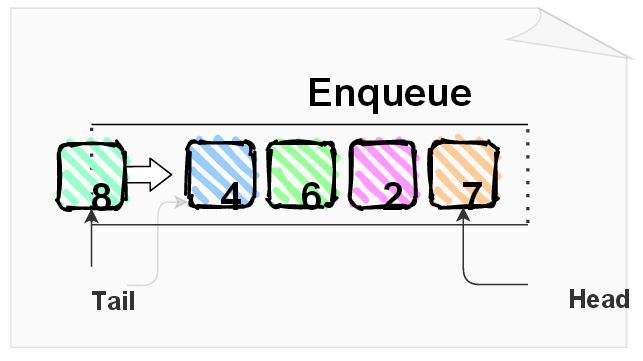
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端( f r o n t \tt front front )进行删除操作,而在表的后端( r e a r \tt rear rear )进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
− \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - −摘自百度百科
长这样☟
队列满足FIFO。[1]
用数组模拟队列
双指针法。
定义两个指针: f r o n t \tt front front 和 r e a r \tt rear rear 。
int front;
int rear;
p u s h ( ) \tt push() push()
把元素装进队列。
把队列想成自动铅笔, p u s h ( ) \tt push() push()就是往笔里塞笔芯。
只需要将 r e a r \tt rear rear ++ 即可。
void push(int x) {
rear ++;
a[rear] = x;
return;
}
e m p t y ( ) \tt empty() empty()
队列是否为空。
通俗的说就是铅笔里还有没有笔芯。
当 r e a r = f r o n t \tt rear = front rear=front 时,队列为空。
bool empty() {
return rear == front;
}
f r o n t ( ) \tt front() front()
获取队头元素值(不删除)。
输出 a [ f r o n t + 1 ] \tt a[front + 1] a[front+1] 即可。
注意:队列为空时无法获取队头元素值。
void front() {
if(empty()) {
printf("error");
return;
}
printf("%d" a[front + 1]);
return;
}
p o p ( ) \tt pop() pop()
删除队头元素。
f r o n t \tt front front ++ 即可。
注意:队列为空时无法删除。
void pop() {
if(empty()) {
printf("error");
return;
}
front ++;
return;
}
c l e a n ( ) \tt clean() clean()
清空队列。
将 r e a r = f r o n t \tt rear = front rear=front 即可。
void clean() {
rear = front;
return;
}
STL里的队列
#include <cstdio>
#include <queue>
using namespace std;
queue<int> q;
int main() {
q.clean();
q.push(1);
printf("%d", q.front());
q.pop();
printf("%d", q.empty());
return 0;
}
输出:
1 1
周末舞会
假设在周末舞会上,男士们和女士们进入舞厅时,各自排成一队。跳舞开始时,依次从男队和女队的队头上各出一人配成舞伴。规定每个舞曲只能有一对跳舞者。若两队初始人数不相同,则较长的那一队中未配对者等待下一轮舞曲。现要求写一个程序,模拟上述舞伴配对问题。
创建两个队列,一个装男士,一个装女士。
int main() {
queue<int> q1;
queue<int> q2;
int n, m, k;
scanf("%d%d%d", &n, &m, &k);
for(int i = 1; i <= n; i ++) {
q1.push(i);
}
for(int i = 1; i <= m; i ++) {
q2.push(i);
}
for(int i = 1; i <= k; i ++) {
printf("%d %d\n", q1.front(), q2.front());
q1.push(q1.front());
q1.pop();
q2.push(q2.front());
q2.pop();
}
}
Blah数集
数学家高斯小时候偶然间发现一种有趣的自然数集合 Blah。对于以 a 为基的集合 Blah 定义如下:
1)a 是集合 Blah 的基,且 a 是 Blah 的第一个元素;
2)如果 x 在集合 Blah 中,则 2x+1 和 3x+1 也都在集合 Blah 中;
3)没有其他元素在集合 Blah 中了。现在小高斯想知道如果将集合 Blah 中元素按照升序排列,第 n 个元素会是多少?注意:集合中没有重复的元素。
开两个队列。
int main() {
queue<int> q1;
queue<int> q2;
int ans, n;
scanf("%d%d", &ans, &n);
int tot = 1;
while(tot != n) {
q1.push(2 * ans + 1);
q2.push(3 * ans + 1);
if(q1.front() < q2.front()) {
ans = q1.front();
q1.pop();
}
else if(q1.front() > q2.front()) {
ans = q2.front();
q2.pop();
}
else {
ans = q1.front();
q1.pop();
q2.pop();
}
tot ++;
}
printf("%d", ans);
return 0;
}
3.STL之栈
S T A C K \tt \ \ \ S \ T \ A \ C \ K S T A C K
“栈( s t a c k \tt stack stack )又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。”
− \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - −摘自百度百科
长这样☟

栈满足LIFO。[2]
就像这摞书,如果你想要拿到最底下那本,你一定需要从上往下一本本拿出来才行。(技术好的也可以釜底抽薪)(大雾)

用数组模拟栈
单指针法。
定义一个指针 r e a r \tt rear rear。
int rear;
p u s h ( ) \tt push() push()
将元素放进栈。
将 r e a r \tt rear rear ++ 并将 x \tt x x 赋值给 a [ r e a r ] \tt a[rear] a[rear] 即可。
void push(int x) {
rear ++;
a[rear] = x;
return;
}
e m p t y ( ) \tt empty() empty()
栈是否为空。
判断 r e a r \tt rear rear 是否为 0 \tt 0 0 即可。
bool empty() {
return rear == 0;
}
t o p ( ) \tt top() top()
获取栈顶元素值(不删除)。
输出 a [ r e a r ] \tt a[rear] a[rear] 即可。
注意:栈为空时无法获取栈顶元素值。
void top() {
if(empty()) {
printf("error");
return;
}
printf("%d", a[rear]);
return;
}
p o p ( ) \tt pop() pop()
删除栈顶元素。
将 r e a r \tt rear rear - - 即可。
void pop() {
rear --;
return;
}
c l e a n ( ) \tt clean() clean()
将栈置空。
将 r e a r \tt rear rear 置为 0 \tt 0 0 即可。
void clean() {
rear = 0;
return;
}
STL中的栈
#include <cstdio>
#include <stack>
using namespace std;
stack<int> s;
int main() {
s.clean();
s.push(1);
printf("%d", q.top());
printf("%d", q.empty());
q.pop();
printf("%d", q.empty());
return 0;
}
输出:
1 0 1
T H E E N D \tt \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \ \ T \ H \ E \quad E \ N \ D T H EE N D
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 新手的第一篇博客,请多多指教。
鸣谢: 重庆八中宏帆初级中学编程社





















 1195
1195











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








