受限玻尔兹曼机和深度置信网络

从玻尔兹曼机到深度置信网络

本文仍处于草稿阶段，请慎重观看

引言

• 受限玻尔兹曼机（Restricted Boltzmann Machines, RBM）最初是在1986年由Paul Smolensky发明，在Geoffrey Hinton和合作者在2005年左右为其发明了快速学习的算法之后，RBM得以进一步发展。RBM可用于可用于降维、分类、回归、协同过滤、特征学习和主题建模。根据任务，RBM可用于监督学习或无监督学习。

• RBM也可用于深度学习网络。具体而言，深度置信网络（Deep Belief Networks）可以通过“堆叠”RBM并可选地通过梯度下降和反向传播来微调网络的参数。

• 本文将从玻尔兹曼机的结构开始介绍，其后引申至受限玻尔兹曼机，最后介绍由受限玻尔兹曼机堆叠而成的深度置信网络。

1. 玻尔兹曼机

玻尔兹曼机(Boltzmann Machine，BM)是一个为整个网络定义“能量”的单元网络。BM的节点产生二元结果（0或1），一个玻尔兹曼机可以表示为带权重的无向图：

由上图可以看出BM的结构为层间、层内全连接。由于每个节点是二值的，所以一共有$2^n$个状态，对于一个节点$x_i$，其值为1 的时候表示这个节点是’on’，其值为0的时候表示这个节点是’off’。

与Hopfield网络不同，玻尔兹曼机节点是随机的。而BM的能量形式与Hopfield网络的形式相同：

$$E=-(\sum_{i<j}w_{ij}s_is_j+\sum_i\theta_is_i)$$
其中， $w_{ij}$为节点 $i$ 和 $j$ 之间的连接权重； $s_i$为节点 $i$ 的状态，其值为0或1；$\theta_i$为节点 $i$的偏置。

1. 1 玻尔兹曼机节点状态概率

BM的全局能量差值由每个节点的状态差值产生，由下式给出：

$$\Delta E_i=E_{i=0}-E_{i=1}$$

2. 受限玻尔兹曼机

无连接约束(层间层内全连接)的波尔兹曼机被证明在机器学习实际问题中效果不佳，但是如果节点的连接受到适当限制，则可以使学习效果足够有效以用于解决实际问题。
受限玻尔兹曼机是玻尔兹曼机的一种变体，区别于玻尔兹曼机，受限玻尔兹曼机可见节点和隐含节点之间存在连接，而隐含节点两两之间以及可见节点两两之间不存在连接，也就是层间全连接，层内无连接。

RBM可以表示成一个二分图模型，所有可见层节点和隐藏层节点都有两种状态：处于激活状态时值为1，未被激活状态值为0。这里的0和1状态的意义是代表了模型会选取哪些节点来使用，处于激活状态的节点被使用，未处于激活状态的节点未被使用。节点的激活概率由可见层和隐藏层节点的分布函数计算。

下面给出RBM模型的数学化定义：
如图1所示，一个RBM包含一个由随机的隐含节点构成的隐藏层(一般是伯努利分布)和一个由随机的可见节点构成的可见层(一般是伯努利分布或高斯分布)。

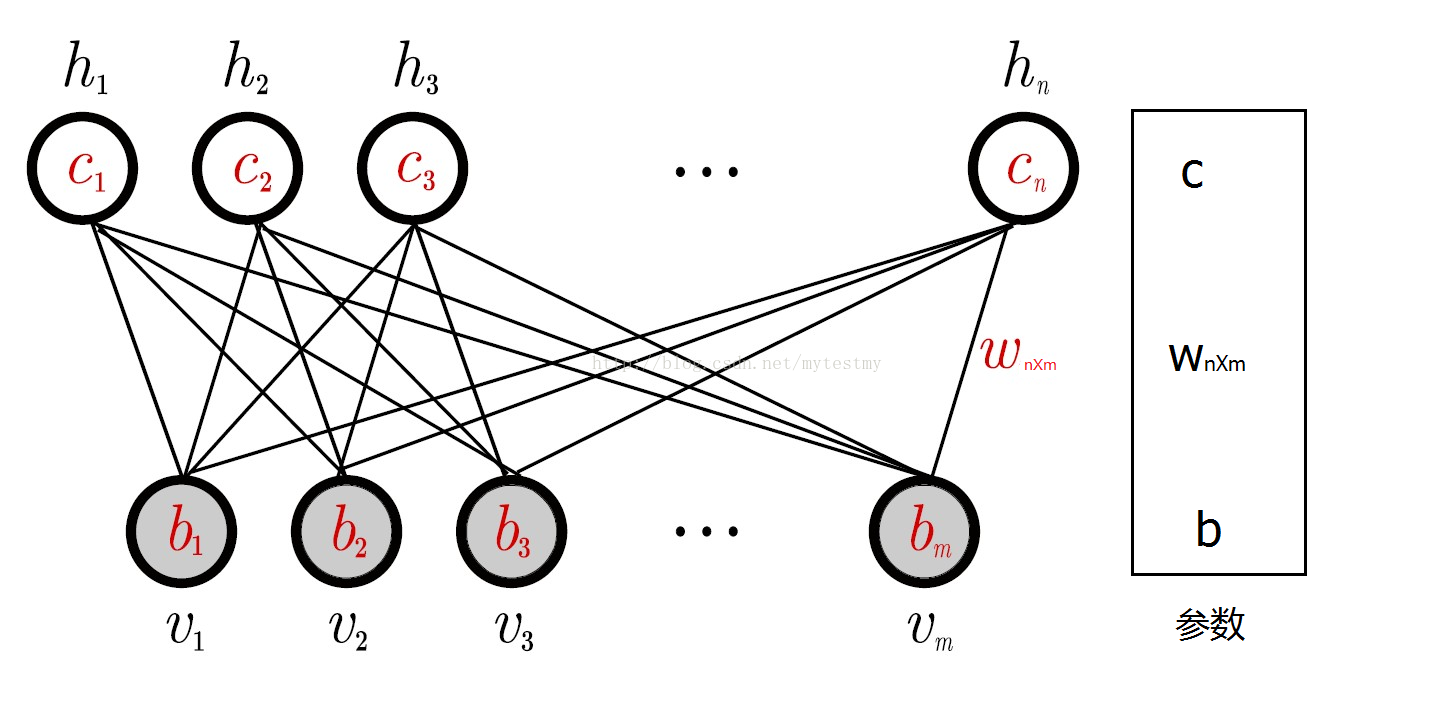
RBM有如下性质：
当给定可见层神经元的状态时，各隐藏层神经元的之间是否激活是条件独立的；反之也同样成立。

2.1 受限玻尔兹曼机参数学习

RBM中，$v$表示所有可见单元，$h$表示所有隐单元。要想确定该模型，只要能够得到模型三个参数$\theta=\{W,A,B\}$即可。分别是权重矩阵$W$，可见层单元偏置$A$，隐藏层单元偏置$B$。
假设一个RBM有$n$个可见单元和$m$个隐单元，用$v_i$表示第$i$个可见单元，$h_i$表示第$j$个隐单元，它的参数形式为：
$W=\{w_{i,j}\in R^{n\times m}\}$ ，其中$W_{i,j}$表示第$i$个可见单元和第$j$个隐单元之间的权值
$A=\{a_i\in R^m\}$ ，其中$a_i$表示第$i$个可见单元的偏置阈值
$B=\{b_j\in R^n\}$ ，其中$b_j$表示第$j$个可见单元的偏置阈值
对于一组给定状态下的$(v, h)$值，假设可见层单元和隐藏层单元均服从伯努利分布，RBM的能量公式是：

$$E(v,h|\theta)=-\sum_{i=1}^n a_iv_i-\sum_{j=1}^mb_jh_j-\sum_{i=1}^n\sum_{j=1}^mv_iW_{ij}h_j$$ 其中， $\theta=\{W_{ij},a_i,b_j\}$是RBM模型的参数，能量函数表示在每一个可见节点的取值和每一个隐藏层节点的取值之间都存在一个能量值。

对该能量函数指数化和正则化后可以得到可见层节点集合和隐藏层节点集合分别处于某一种状态下$(v,h)$联合概率分布公式：

$$P(v,h|\theta)=\frac{e^{-E(v,h|\theta)}}{Z(\theta)}$$ $$Z(\theta)=\sum_{v,h}e^{-E(v,h|\theta)}$$ 其中， $Z(\theta)$为归一化因子或配分函数（partition function），表示对可见层和隐藏层节点集合的所有可能状态的能量指数求和。

对于参数的求解往往采用似然函数求导的方法。已知联合概率分布$P(v,h|\theta)$，通过对隐藏层节点集合的所有状态求和，可以得到可见层节点集合的边缘分布$P(v|\theta)$：

$$P(v|\theta)=\frac{1}{Z(\theta)}\sum_he^{-E(v,h|\theta)}$$ 边缘分布表示的是可见层节点集合处于某一种状态分布下的概率。

由于RBM模型的特殊的层间连接、层内无连接的结构，它具有以下重要性质：
1）在给定可见单元的状态时，各隐藏层单元的激活状态之间是条件独立的。此时，第$j$个隐单元的激活概率为：

$$P(h_j=1|v)=\sigma(b_j+\sum_iv_iW_{ij})$$ 2）相应的，当给定隐单元的状态时，可见单元的激活概率同样是条件独立的：

$$P(v_i=1|h)=\sigma(a_i+\sum_jW_{ij}h_j)$$ 其中， $\sigma(x)=\frac{1}{1+exp(-x)}$是sigmoid函数，其函数曲线如下图所示：

采用该函数用作每一层节点的激活概率公式的原因是：sigmoid函数的定义域是 $(-\infty,+\infty)$，值域处于$(0,1)$之间。也就是说，无论模型的可见层输入节点数据处于一个多大的范围内，都可以通过sigmoid函数求得它相应的函数值，并且该函数值被压缩于0到1之间，即节点的激活概率值。

2.2 受限玻尔兹曼机模型参数求解

确定RBM模型需要求解模型的三个参数$\theta=\{W_{ij},a_i,b_j\}$，下面围绕参数的求解进行分析。

参数求解使用对数似然函数对参数求导。
从$P(v|\theta)=\frac{1}{Z(\theta)}\sum_he^{-E({v,h|\theta})}$可知，能量$E$和概率$P$成反比，通过最大化$P$来最小化$E$。最大化似然函数常用方法是梯度上升法，梯度上升法是指按照以下公式对参数进行修改：

$$\theta=\theta+\mu\frac{\partial lnP(v)}{\partial\theta}$$ 通过求 $lnP(v)$关于 $\theta$的导数，即 $\Delta\theta$，然后对原 $\theta$值进行修改。如此迭代使似然函数 $P$最大，从而使能量$E$最小。
对数似然函数的格式： $lnP(v^s)$， $v^s$表示模型的输入数据，此处先对单个样本进行分析，即 $v^s$为数据集中第 $s$个样本。
然后对$\{W_{ij},a_i,b_j\}$里的参数分别进行求导，详细的推导过程就不写了： $$\frac{\partial lnP(v^s)}{\partial w_{i,j}}=P(h_i=1|v^s)v_j^s-\sum_vP(v)P(h_i=1|v)v_j$$
$$\frac{\partial lnP(v^s)}{\partial a_i}=v_i^s-\sum_vP(v)v_i$$
$$\frac{\partial lnP(v^s)}{\partial b_i}=P(h_i=1|v^s)-\sum_vP(v)P(h_i=1|v)$$ 由于上面三式的第二项中都含有 $P(v)$， $P(v)$中仍然含有参数，所以它是式中求不出来的。所以，有很多人就提出了一些通过采样逼近的方法来求每一个式子中的第二项，如Gibbs采样法，关于采样方法将另开一篇文章介绍，在此不做详述。

2.3 模型训练算法

通过常规的MCMC采样法来估计上面的式子的未知项十分缓慢，最大原因在于需要经过很多步的状态转换才能保证采集到的样本符号目标分布。既然我们的目标是让RBM拟合训练样本的分布，那么是否可以考虑让MCMC的状态以训练样本作为起点呢？这样一来也许这些状态只需要很少次数的状态转换就可以抵达RBM的分布了。 基于这个想法，Hinton教授于2002年发明了对比散度算法（Contrastive Divergence，CD)，该方法目前已成为训练RBM的标准算法。
k步CD算法（CD-k）具体可描述为：对$\forall v\in S$，取初始值$v^{(0)}:=v$，然后执行k次采样：
for t = 1,2,3,……,k:
    利用$P(h|v^{(t-1)})$ 采样出$h^{(t-1)}$
    利用$P(v|h^{(t-1)})$ 采样出$v^{(t)}$
接着，利用k次采样后得到的$v^{(k)}$ 来估计2.2中的三个公式$\frac{\partial lnP(v^t)}{\partial w_{i,j}}$、$\frac{\partial lnP(v^t)}{\partial a_i}$、$\frac{\partial lnP(v^t)}{\partial b_j}$，具体为：

$$\frac{\partial lnP(v)}{\partial w_{i,j}}\approx P(h_i=1|v^{(0)})v_j^{(0)}-P(h_i=1|v^{(k)})v_j^{(k)}$$
$$\frac{\partial lnP(v)}{\partial a_i}\approx v_i^{(0)}-v_i^{(k)}$$
$$\frac{\partial lnP(v)}{\partial b_i}\approx P(h_i=1|v^{(0)})-P(h_i=1|v^{(k)})$$
至此，梯度计算公式都变得具体可算了。

2.3.模型的评估

对于已经学习或者正在学习的RBM，评价其优劣的指标常用重构误差（reconstruction error），即以训练样本作为初始状态，经过RBM的分布进行一次Gibbs转移后与原数据的差异量，具体为：

重构误差能在一定程度上反映RBM对训练样本的似然度，不过并不完全可靠。但其计算较简单，在实践中非常有用。
另外还有一种叫退火式重要性抽样也可计算RBM对训练数据的似然度。

3 深度置信网络

深度置信网络（Deep Belief Nets，DBN）神经网络的一种。既可以用于非监督学习，类似于一个自编码机；也可以用于监督学习，作为分类器来使用。

从非监督学习来讲，其目的是尽可能地保留原始特征的特点，同时降低特征的维度。从监督学习来讲，其目的在于使得分类错误率尽可能地小。而不论是监督学习还是非监督学习，DBN的本质都是Feature Learning的过程，即如何得到更好的特征表达。

一个DBN模型由若干个RBM堆叠而成，训练过程由低到高逐层进行训练，其结构如下图所示：

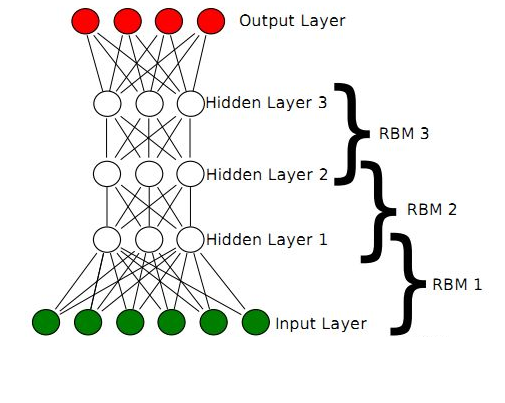
回想一下RBM，由可见层、隐层组成，可见单元用于接受输入，隐含单元用于提取特征，因此隐含单元也有个别名，叫特征检测器。也就是说，通过RBM训练之后，可以得到输入数据的特征。
另外，RBM还通过学习将数据表示成概率模型，一旦模型通过无监督学习被训练或收敛到一个稳定的状态，它还可以被用于生成新数据。

正是由于RBM的以上特点，使得DBN逐层进行训练变得有效，通过隐层提取特征使后面层次的训练数据更加有代表性，通过可生成新数据能解决样本量不足的问题。逐层的训练过程如下：
（1）最底部RBM以原始输入数据进行训练
（2）将底部RBM抽取的特征作为顶部RBM的输入继续训练
（3）重复这个过程训练以尽可能多的RBM层

Hinton提出，这种预训练过程是一种无监督的逐层预训练的通用技术，也就是说，不是只有RBM可以堆叠成一个深度网络，其它类型的网络也可以使用相同的方法来生成网络。

参考文献

[1]https://www.cnblogs.com/jhding/p/5687696.html [2]https://blog.csdn.net/u010223750/article/details/60882390
[3]https://blog.csdn.net/itplus/article/details/19408143
[4]Hinton G. A practical guide to training restricted Boltzmann machines[J]. Momentum, 2010, 9(1): 926.
[5]Bengio Y, Lamblin P, Popovici D, et al. Greedy layer-wise training of deep networks[J]. Advances in neural information processing systems, 2007, 19: 153.
[6]Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural computation, 2006, 18(7): 1527-1554.
[7]https://en.wikipedia.org/wiki/Restricted_Boltzmann_machine
[8]https://blog.csdn.net/Rainbow0210/article/details/53010694?locationNum=1&fps=1
[9]https://my.oschina.net/u/876354/blog/1626639