截图均来自3Blue1brown博客课程
文章目录
一、正态分布为什么用e负x平方 e − x 2 e^{-x^{2}} e−x2
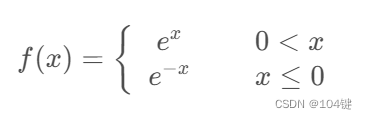
在 x = 0 x=0 x=0处轴对称，但是在 x = 0 x=0 x=0处不可导（左导数为-1 ≠ \neq =右导数为1，不可导）
f ( x ) = e − x 2 f(x)=e^{-x^{2}} f(x)=e−x2
当用x平方时，左右仍然对称，且在 x = 0 x=0 x=0处可导（左右导数均为1）。
此时，函数形状为倒扣钟形，并且可以进行从负无穷到正无穷的积分。
二、 π \sqrt{\pi} π根号pi怎么求
令 A r e a = C = ∫ e − x 2 d x Area = C=\int e^{-x^{2}}dx Area=C=∫e−x2dx，
又 V o l u m n = ∫ e − y 2 e − x 2 d x = ∫ C e − x 2 d x = C 2 Volumn = \int e^{-y^{2}}e^{-x^{2}}dx = \int Ce^{-x^{2}}dx=C^{2} Volumn=∫e−y2e−x2dx=∫Ce−x2dx=C2
则求解出Volumn即可得Area，即C。
令 r= x 2 + y 2 \sqrt{x^2+y^2} x2+y2(极坐标)，则Volumn用极坐标表示：
即求取柱形体积，有厚度 d r dr dr，周长 2 π r 2\pi r 2πr，高 e − r 2 e^{-r^{2}} e−r2，
则对于整个钟形体积有：
∫ 2 π r e − r 2 d r = π \int2\pi re^{-r^{2}}dr=\pi ∫2πre−r2dr=π
即Volum= π \pi π，可得Area= π \sqrt{\pi} π
最低0.47元/天 解锁文章
扫一扫
2952
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
