文章目录
之前有一篇关联的时间序列笔记,【回顾︱时间序列预测与分解有哪些模型?(一)】,本篇将笔者看到比较好的方案、案例都贴出来,持续更新
时间序列预测任务旨在基于过去的观察值以及潜在的协变量来预测目标系列的未来值,涉及多个核心概念:
- 回顾窗口(Look-back Window):指目标时间序列中最近 L 个时间步的连续观测值,作为主要的历史上下文信息来源,用于建模趋势、季节性和其他时间依赖关系。
- 协变量(Covariates / 外生变量):除目标序列外,许多应用还利用气象、经济或人口等外部因素作为辅助输入。这些变量有助于提升模型对外部驱动因素的建模能力。
- 预测窗口(Predicted Window):预测任务的输出通常是一段未来时间步,长度可以从单步(如下一小时)到多步(如下一周或下月)不等。
- 单步 vs 多步预测(One-step vs. Multi-step):单步预测每次仅预测一个未来时间点,适用于逐步滚动预测;多步预测则一次性输出多个未来时间点,能够建模长期依赖,但可能引入更大的误差累积。
- 单变量 vs 多变量预测(Univariate vs. Multivariate):单变量预测仅依赖目标序列本身;多变量预测则引入多个相关序列或协变量,以挖掘跨序列间的依赖关系,从而提升精度。
- 迭代 vs 直接预测策略(Iterative vs. Direct Strategies):迭代策略逐步生成未来值,并将其作为输入用于后续预测;直接策略则为每个未来时间步构建独立的预测机制,可减少误差传播,但建模难度更高。
- 点预测 vs 概率预测 (Point vs. Probabilistic Forecasting): 根据预测结果的性质,时序预测任务可以划分为点预测(非概率)和概率预测,前者为每个时间步生成一个确定性的预测,而后者挖掘数据中的固有不确定性以生成对未来值分布的预测。
文章目录
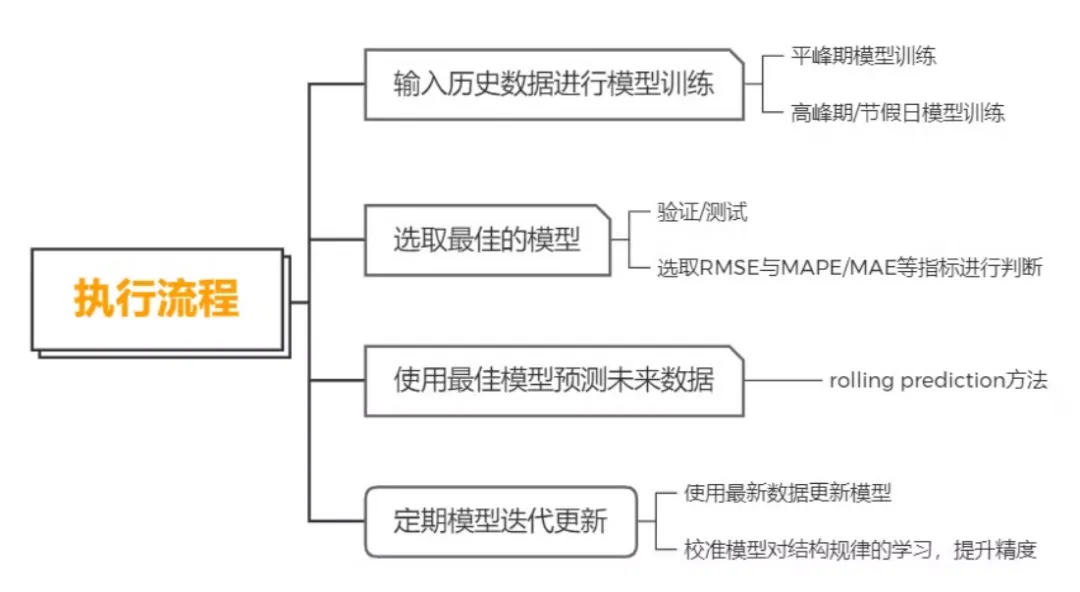
1 应用案例
1.1 蚂蚁集团的时间序列 AI 技术实践与应用探索
https://mp.weixin.qq.com/s/vYqqYNQPnb-XFQ0QuYLkqQ
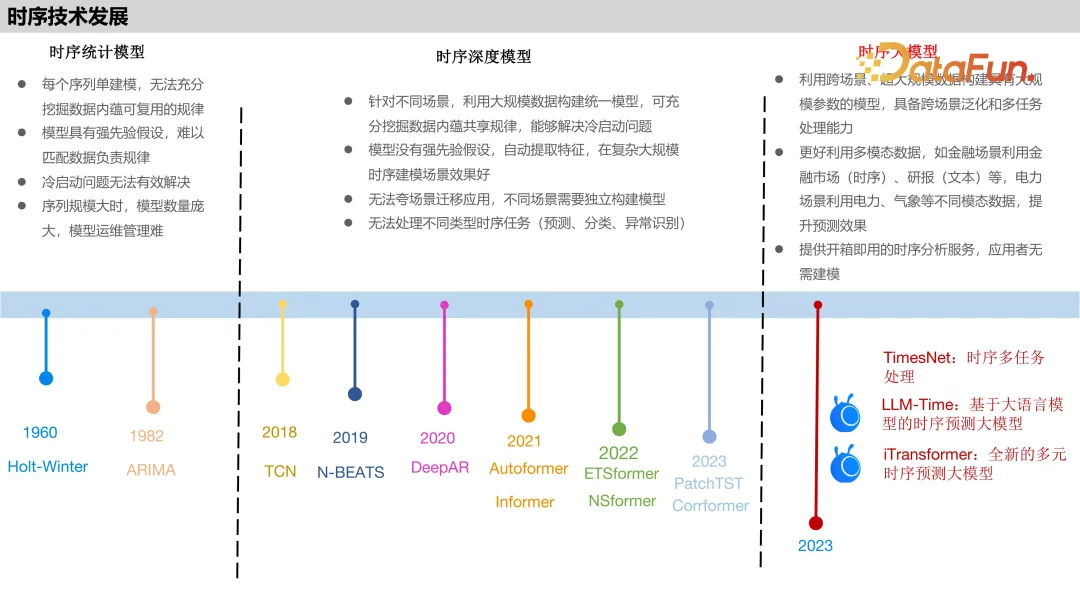
蚂蚁自研的时序预测算法总纲,这些算法都是为了解决一些业务中存在的问题:
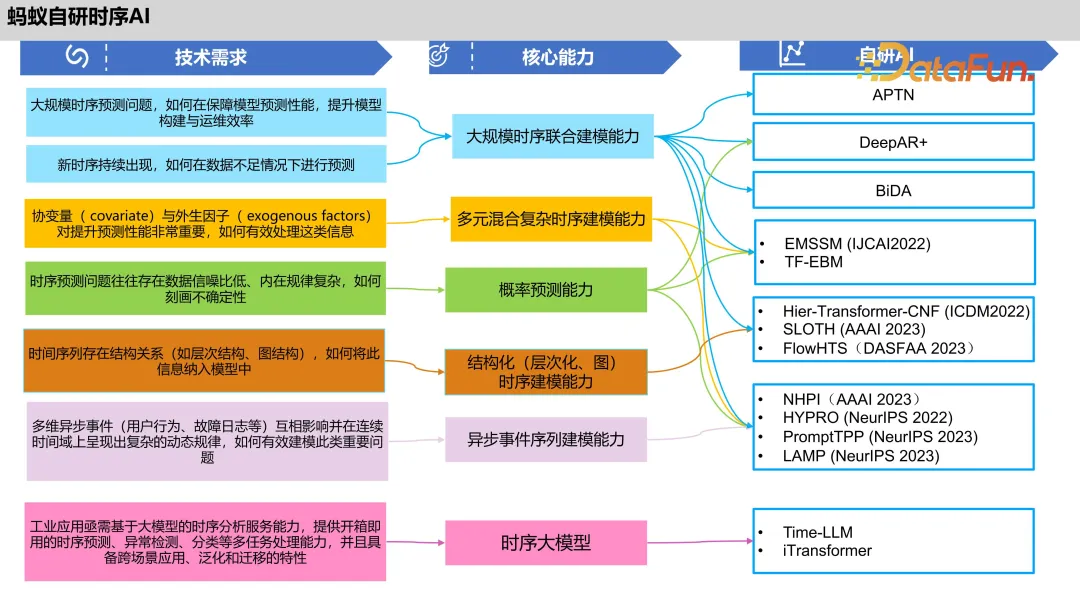
AntFlux 是蚂蚁集团的一个时序平台,主要包括下面几个模块:
- Insight 时序洞察:主要用于时序分析,比如异常检测、数据处理特征、时序特征生成。
- Forecaster 同步时序建模:具有丰富的时序算法,用于自动化地构建模型。
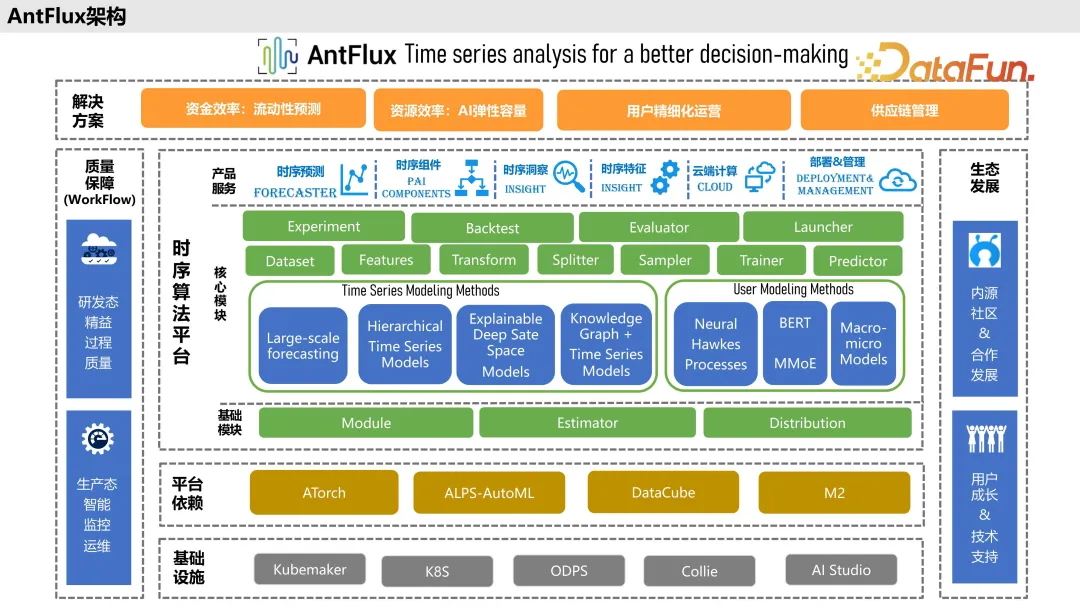
竞品对比
1.2 结构化多元时序模型在携程业务量上的预测应用
结构化多元时序模型在携程业务量上的预测应用
BSTS结构模型也是一种针对结构化时序数据的模型,能够拆解出数据背后的结构因子。
最终给出的预测结果也都是包含置信区间的“区间估计”,不能满足业务方想要一个“具体预测值”的需求。且BSTS模型普遍情况下适合单维变量的预测情况,不能很好地捕捉到不同变量之间的相关性。
SCNN模型(Structured Components-based Neural Network)全称为“基于结构化组件的神经网络模型”,正如其名,它的主要特点体现在:
- (1)将数据分解为多个结构;
- (2)适用于多元序列数据;
- (3)应用了神经网络的建模思想。
某一个时序数据通过SCNN拆解后得到的4个模块,最上方的蓝线表示原有的数据,下方的四种曲线分别表示一种结构。
将时序数据分为4个模块:
- 长周期项(long-term);长周期反映的是序列数据在较长时间范围内的变化
- 短周期项(short-term);较短的窗口能够防止一些短期内的信息平滑掉,从而能够体现出数据在短时间内的变化,提供更全面的信息
- 季节性项(seasonal-component):与长周期项的滑动窗口类似,在基于 “序列的周期长度是一致的”假设前提下,对季节性项也采取一个窗口统计的方法
- 序列间相关性项(co-evolving component):需要识别出哪些序列间会共享同一个相关性结构,换句话说我们需要知道每一对序列之间的相关性结构
原文还有一个案例
考虑到春节的特殊性,我们选择从2024年3月1日起进行模型的验证:用每168H的数据来预测下一个24H的业务量(例如用3/1~3/7的数据预测3/8的数据),并采取rolling prediction的方式对36月的每日业务量数据进行预测(用3/13/7的数据预测3/8的数据,随后用3/2~3/8的数据预测3/9的数据)。过程中并未用到任何实际真实的数据,完全是通过模型预测完成了对3个月内每天业务量的预测任务。整个预测期间会涉及清明、五一与端午三个节假日,我们会在平峰期时使用平峰期SCNN模型;
1.2.2 深度多元时序模型在携程关键指标预测场景下的探索应用
预测目标值:流量、订单量和GMV等关键指标。
预测时长:未来30天。
时间序列预测模型大致可分为三类:
- 一是传统时间序列预测模型,比如移动平均、ARIMA、指数平滑法等,
- 二是机器学习模型,比如线性回归、树模型、Prophet等,
- 三是深度学习模型,比如时序卷积网络(TCN)、LSTM、Transformer等。
传统时间序列预测模型处理多步预测时,往往采用滚动预测的策略,即使用前一期预测值作为实际值加入模型,从而得到下一期的预测,这种策略会导致预测误差累计,从而使得多步预测的精准性越来越差。
几种Transformer变种的模型:
- Informer,解决传统的时间序列预测模型在长序列和多尺度预测上的挑战,以便模型能够更好地捕捉序列中的长期依赖关系和全局上下文信息
- Autoformer,Informer的进化版,修复长序列中的复杂时间模式使得注意力机制难以发现可靠的时序依赖
- DLinear,时序上的位置信息在时序预测中时十分重要的,因此提出DLinear模型,在Autoformer 的分解层后面加上全连接层。模型使用分解层将输入时间序列分解为残差部分(季节性)和趋势部分。
- TimesNet,全新的多周期视角分析时序变化,一维时间序列通过快速傅里叶变换选取多个周期,基于多个周期对一维数据进行折叠,得到多个二维张量,每个二维张量的列和行分别反应了周期内与周期间的时序变化
模型部署与回测:

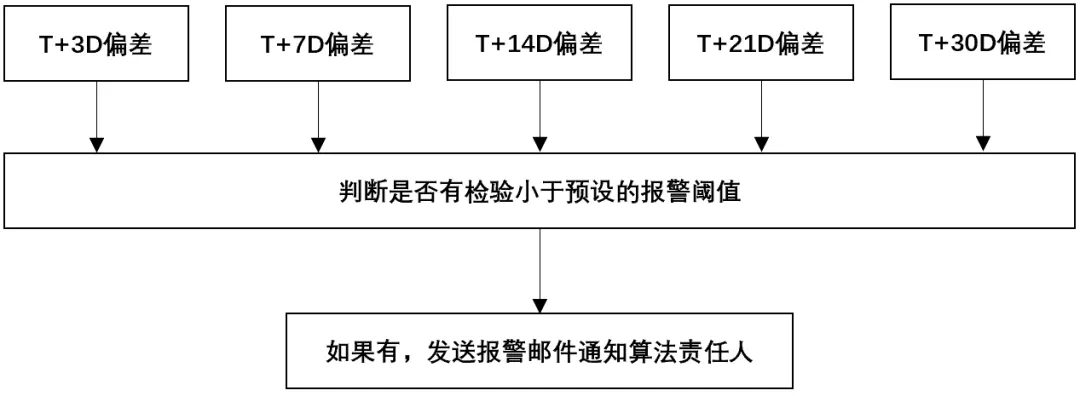
模型上线后需要一定的监控机制,以便在模型预测的效果不好的时候及时修正模型。我们持续监控预测值和真实值的T+3D、T+7D、T+14D、T+21D、T+30D偏差,并以报表的形式展现。
1.3 季节性的分析才不简单,小心不要在随机数据中也分析出季节性
干货 | 季节性的分析才不简单,小心不要在随机数据中也分析出季节性
文章比较啰嗦,大概:
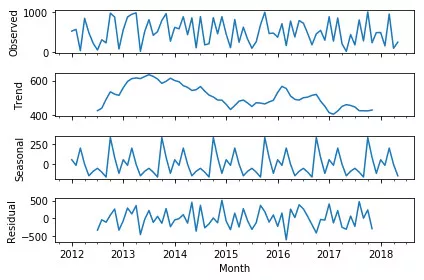
结论一:通过statsmodels 的包分解出来的季节性,不论什么数据都拥有所谓的季节性,即使是0 到 1000 之间随机数据点组成的时间序列,并对其进行了分解,也会拥有季节性:
结论二:季节性在时间序列分析中可能并不重要,因为影响没有想象那么大
1.4 网易游戏:基于时间序列的玩家行为模式分析
文章提出了基于用户行为时间序列的一种特别的优化距离算法,从而利用它让基于时序的用户聚类变得更加合理
平滑化序列的欧式距离(SEUD)

使用SEUD作为时间序列的距离定义,保持了欧式空间的几何性质,使得大部分聚类算法都可以应用,可以根据数据规模与产品特性选择。
9 其他时间序列算法文章
9.1 五类常见时序特征代码
https://mp.weixin.qq.com/s/riPx10eWErMPeolzxBnWew
五类强悍时序特征:
- Date and Time Features and Domain-Specific Features;这类特征一般可以用于捕捉周期性的信息,以及一些突发的情况,例如节假日等信息
- 滚动聚合特征:滚动窗口和扩展窗口统计涉及在移动或逐渐变大的固定大小窗口上计算摘要统计数据,如平均值、中位数、标准偏差以及最大或最小值。
- 指数平滑:指数平滑给过去的观察分配指数递减的权重,更加强调最近的观察
- Lag特征:Lag特征是指时间序列中先前时间步的值
- 季节性分解特征:季节性分解将时间序列分离为:趋势;季节;残差
def extract_date_features(data):
data['Year'] = data.index.year
data['Month'] = data.index.month
data['Day'] = data.index.day
data['Weekday'] = data.index.weekday
data['Day_of_year'] = data.index.dayofyear
data['Week_of_year'] = data.index.isocalendar().week
data['Quarter'] = data.index.quarter
data['Is_month_start'] = data.index.is_month_start
data['Is_month_end'] = data.index.is_month_end
data['Is_quarter_start'] = data.index.is_quarter_start
data['Is_quarter_end'] = data.index.is_quarter_end
data['Is_year_start'] = data.index.is_year_start
data['Is_year_end'] = data.index.is_year_end
data['Days_in_month'] = data.index.days_in_month
data['Is_leap_year'] = data.index.is_leap_year
data['Elapsed_days'] = (data.index - data.index.min()).days
data['Weekday_name'] = data.index.day_name()
data['Month_name'] = data.index.month_name()
data['Is_weekend'] = data['Weekday'].apply(lambda x: x >= 5)
data['Is_weekday'] = ~data['Is_weekend']
data['Days_till_month_end'] = data['Days_in_month'] - data['Day']
data['Days_since_month_start'] = data['Day'] - 1
data['Week_of_month'] = (data['Day'] - 1) // 7 + 1
data['Weekday_of_month'] = (data['Day'] - 1) % 7 + 1
data['Days_to_next_holiday'] = data.index.to_series().apply(lambda x: (x + pd.DateOffset(days=1)).to_period('D').start_time)
data['Days_since_last_holiday']= data.index.to_series().apply(lambda x: (x - pd.DateOffset(days=1)).to_period('D').end_time)
data['Business_days_in_month'] = data.index.to_series().apply(lambda x: np.busday_count(x.replace(day=1), x.replace(day=x.days_in_month) + pd.DateOffset(days=1)))
data['Business_day_of_month'] = data.index.to_series().apply(lambda x: np.busday_count(x.replace(day=1), x))
data['Days_since_first_day_of_year'] = data['Day_of_year'] - 1
data['Days_remaining_in_year'] = (data.index + pd.offsets.YearEnd(0)).dayofyear - data['Day_of_year']
return data
9.2 时间序列数据特征提取的几类方法
领域特定特征提取: 考虑特定的问题。例如,假设正在处理一个工程实验的信号,我们真正关心的是t = 6s后的振幅。这些是特征提取在一般情况下并不真正有意义,但对特定情况实际上非常相关。这就是我们所说的领域特定特征提取。
基于频率的特征提取:
时间序列/信号的谱分析有关,将其转换为频率域。 信号有三个周期性组件。频率域的想法是将信号分解为其周期性组件的频率、振幅和相位。
两种常见拆解方式:傅里叶变换(基于正弦/余弦函数) + 小波分解(基于小波)
基于统计的特征提取
特征提取的另一种方法是依靠统计学。偏度和峰度。分位数。自相关。熵。方差。平均值
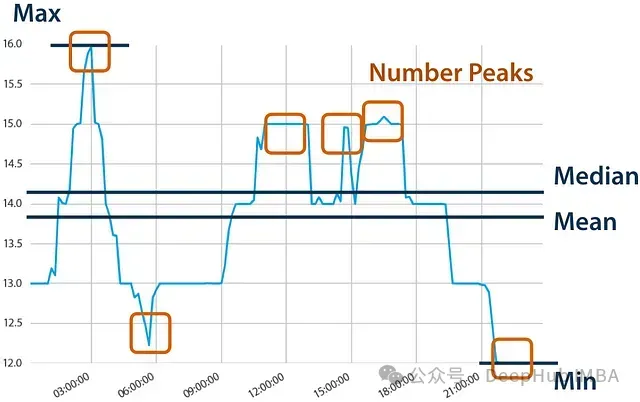
基于时间的特征提取器
提取时间特征来提取时间序列的信息。比如提取峰值和谷值的信息
将使用来自SciPy的find_peaks函数。
import numpy as np
from scipy.signal import find_peaks
def extract_peaks_and_valleys(y, N=10):
# Find peaks and valleys
peaks, _ = find_peaks(y)
valleys, _ = find_peaks(-y)
# Combine peaks and valleys
all_extrema = np.concatenate((peaks, valleys))
all_values = np.concatenate((y[peaks], -y[valleys]))
# Sort by absolute amplitude (largest first)
sorted_indices = np.argsort(-np.abs(all_values))
sorted_extrema = all_extrema[sorted_indices]
sorted_values = all_values[sorted_indices]
# Select the top N extrema
top_extrema = sorted_extrema[:N]
top_values = sorted_values[:N]
# Pad with zeros if fewer than N extrema are found
if len(top_extrema) < N:
padding = 10 - len(top_extrema)
top_extrema = np.pad(top_extrema, (0, padding), 'constant', constant_values=0)
top_values = np.pad(top_values, (0, padding), 'constant', constant_values=0)
# Prepare the features
features = []
for i in range(N):
features.append(top_values[i])
features.append(top_extrema[i])
# Create a dictionary of features
feature_dict = {f'peak_{i+1}': features[2*i] for i in range(N)}
feature_dict.update({f'loc_{i+1}': features[2*i+1] for i in range(N)})
return feature_dict,pd.DataFrame([feature_dict])
# Example usage:
x = np.linspace(-2*np.pi,2*np.pi,1000)
y = np.sin(x) + 0.4*np.cos(2*x) + 2*np.sin(3.2*x)
features = extract_peaks_and_valleys(y, N=10)
features[1]
9.3 18 种高效工具库及其应用分析
tsfresh 是一个综合性的时间序列特征提取框架,其核心优势在于能自动计算数百种特征,并通过统计检验方法筛选出最相关且非冗余的特征子集。
tsfel(时间序列特征提取库)是另一个专业的时间序列特征提取 Python 库,提供了全面的特征提取功能。
tsfel 的特征体系分为四个主要类别:统计类特征(如熵测量、基于直方图的特征)、时域特征(如自相关系数)、频域特征(如功率谱密度)以及分形特征(如去趋势波动分析)。这种多维度的特征体系使其能够捕捉时间序列的不同方面。
pywavelets
PyWavelets 是一个专业的小波变换库,提供了全面的小波分析工具,包括正向和逆向离散小波变换、连续小波变换等多种变换方法。
ta-lib
ta-lib 是一个专为金融时间序列技术分析设计的库,包含了数百种技术指标,例如广泛应用的移动平均收敛/发散 (MACD) 和相对强度指数 (RSI) 等。
虽然 ta-lib 主要面向金融领域,但其技术指标和特征提取方法同样适用于其他类型的时间序列分析。ta-lib 中的许多特征专门设计用于应对金融时间序列中常见的高噪声环境,这一特性使其在处理其他领域的噪声数据时也具有应用价值。
Featuretools
Featuretools 包含了多种基于事件的特征提取方法:
时间间隔特征,如自上次特定值或统计量(最大值、最小值等)出现以来的时间
基于计数的指标,如大于特定阈值的连续值数量
时间相关特征,如与节假日的距离(天数)
9.4 行业SOTA,京东首个自研十亿级时序大模型揭秘
https://mp.weixin.qq.com/s/FiRjmFyDrFl0CWf4XppCRg
TPO方案的主要创新点:
- 首次将人类反馈的强化学习(RLHF)应用于销量预测领域:这标志着强化学习技术在时间序列预测中的首次大规模应用。
- 专为纯时序大模型设计强化学习框架:由于时序大模型的输入输出是连续数值,且传统时序模型常采用均方误差(MSE)或分位数损失,导致无法直接进行时序差分(TD)误差计算或输出预测值的概率(难以计算概率及KL散度),因此传统的PPO、RLOO等强化学习框架不适用。TPO通过引入适用于纯时序大模型的强化学习框架来解决这些问题。
- 包含概率预测组件:TPO框架融入了概率预测功能,这在传统时序模型中通常是缺失的。
- 设计了独特的优势函数和时序损失:为了适应时间序列的特性和强化学习的需求,TPO方案中设计了专门的优势函数和时序损失。
输入数据包括:
- 时序数据:连续的多维时间序列,例如销量、价格、库存等指标
- 状态表示:使用Transformer编码后的隐藏状态作为环境状态
- 人类反馈:专家对预测结果的评价和偏好数据
优势函数设计
- GAE (Generalized Advantage Estimation):结合即时奖励和长期价值估计
- 多步奖励:考虑时序预测的多步特性,使用折扣因子计算累积奖励
- 标准化:对优势函数进行标准化,提高训练稳定性
时序损失设计
TPO的损失函数包含四个主要组件:
总损失 = 策略损失 + α×价值损失 + β×熵正则化 + γ×MSE损失
- 策略损失:使用PPO风格的裁剪损失,适应连续动作空间
- 价值损失:训练价值网络准确估计状态价值
- 熵正则化:鼓励探索,防止策略过早收敛
- MSE损失:保持预测准确性,这是时序模型的核心目标
9.5 首个「万亿级时间点」预训练,清华发布生成式时序大模型日晷 | ICML Oral
https://mp.weixin.qq.com/s/y3sc2e2lmW1sqfnoK-ZdDA
论文链接:https://arxiv.org/pdf/2502.00816
代码链接:https://github.com/thuml/Sundial
开源模型:https://huggingface.co/thuml/sundial-base-128m
时序Transformer+流匹配生成
日晷模型主体为可扩展Transformer,使用重归一化,分块嵌入和多分块预测等技术适配时序数据特性,并融入了FlashAttention,KV Cache等进行效率优化。
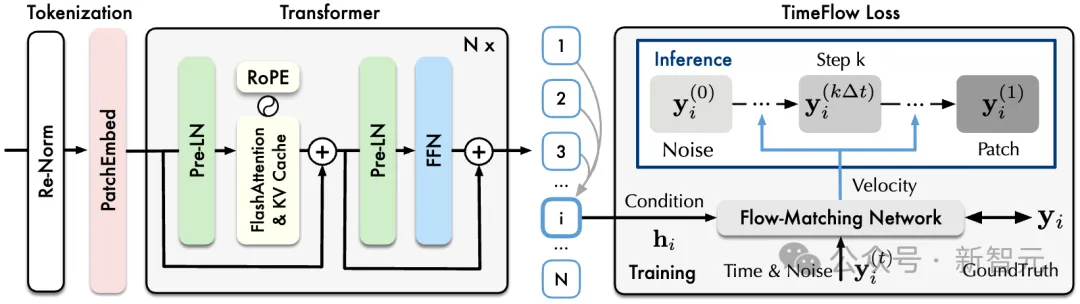
最终的效果其实是生成一段数据集,感觉局限性、自由度不高
9.6 TimeReasoner:让大模型慢慢“思考”,时间序列预测的新范式
https://mp.weixin.qq.com/s/YF7nd9VuBf5r1-4t_prTcw
【论文地址】
https://arxiv.org/abs/2505.24511
【代码仓库】
https://github.com/realwangjiahao/TimeReasoner
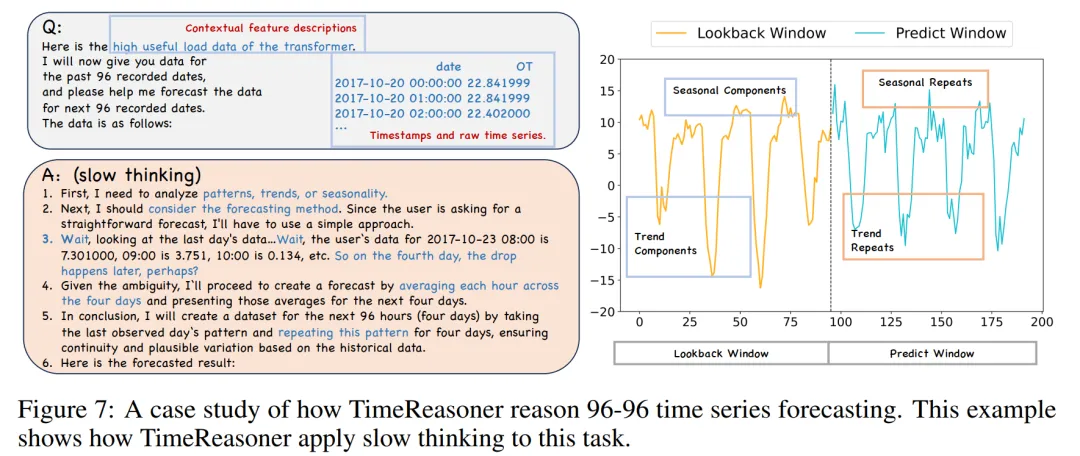
TimeReasoner 的内部推理过程大致可分为三个阶段:数据分析与模式识别、预测策略评估、反思与上下文评估。此外,推理过程中使用的 Token 数量(代表推理深度)与预测性能(以 MSE 衡量)相关,更高的 Token 数通常对应更低的 MSE。案例研究(如图8所示)清晰展示了 LLM 如何模仿人类专家进行“慢思考”推理,先分析数据模式,然后进行详细分析,确定使用模型,最终得到预测结果。
9.7 Python开源工具tempdisagg:轻松搞定时间序列分解,经济预测更精准!
https://mp.weixin.qq.com/s/fE6xDg2Cm0W6tXAO6VBSng
【论文标题】
tempdisagg: A Python Framework for Temporal Disaggregation of Time Series Data
【论文地址】
https://arxiv.org/html/2503.22054v1#S3
【代码资源库】
https://github.com/jaimevera/tempdisagg
然而,现有工具要么操作复杂,要么功能单一。来自哥伦比亚大学的研究者推出的 tempdisagg 框架,集成了8种经典计量经济学算法,并创新性地引入机器学习优化策略,成为 Python 生态中首个“开箱即用”的工业级解决方案。
除了重现 Chow-Lin、Denton、Fernández 和 Litterman 等经典方法外,该软件包还引入了集成建模能力和估计后调整功能,使用户能够提高模型的稳健性,并满足现实世界的约束条件,例如非负性和聚合一致性。这些特性使得 tempdisagg 在国家统计、政策评估和经济预测等领域的应用中尤为宝贵。
经典算法支持
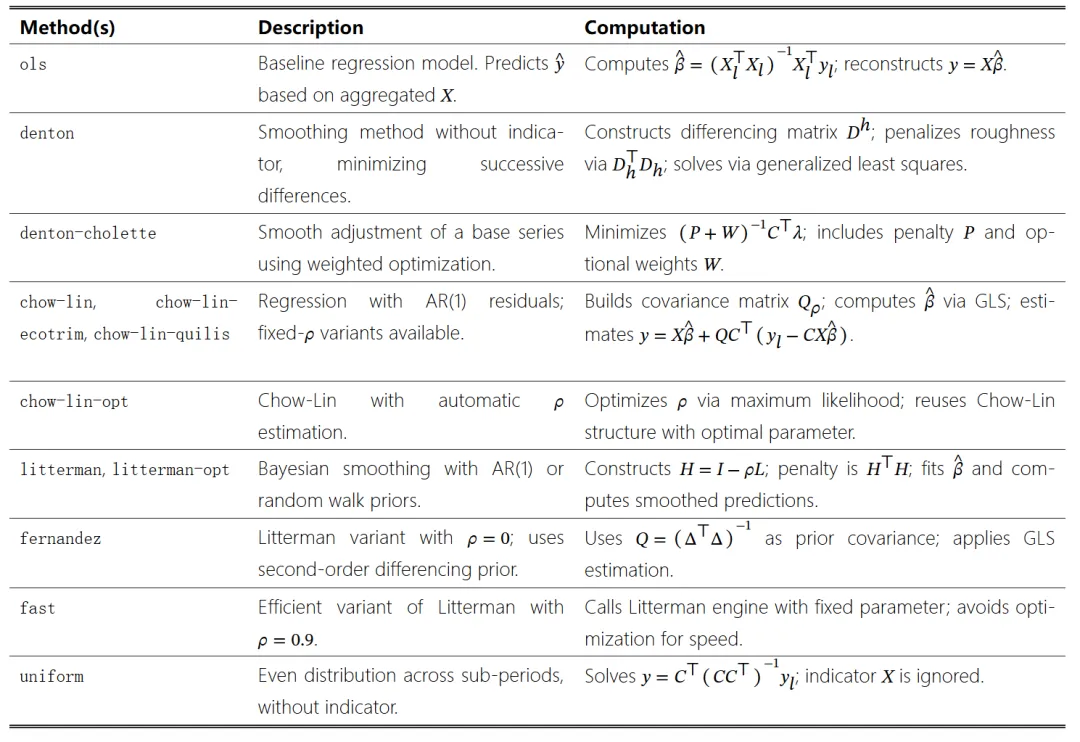
创新功能
- ρ参数自动优化:通过最大似然估计或残差最小化自动确定最优自相关系数。
- 负值校正系统:GDP、人口等指标不能为负,工具自动调整并保持总量一致。
- 逆向填充模块:独有的 Retropolarizer 模块,通过比例调整、回归或神经网络补全缺失低频数据。
- 集成建模引擎:通过非负最小二乘法融合多个模型的预测结果,鲁棒性提升35%。

























 1547
1547

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








