K近邻（KNN）算法、KD树及其python实现

1、k近邻算法

KNN基本思想

k近邻法是基本且简单的分类与回归方法，即对于输入实例，依据给定的距离度量方式（欧式距离），以及选择合适的k值（交叉验证），在样本集中找到最近邻新实例的k个样例，通过k个最近邻样例的类别表决出新实例的类别（多数表决）。当k为1时，称为最近邻。

K近邻法是基于样本集对特征空间的一个划分，没有显式的学习过程。k近邻模型由 距离度量、k值选择和分类决策规则决定。

图1 kNN算法基本思想

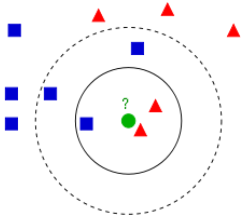
距离度量

特征空间中两个特征向量${\mathbf{x}}_i=(x_i^1,x_i^2,\cdots ,x_i^n)$和${\mathbf{x}}_j=(x_j^1,x_j^2,\cdots ,x_j^n)$的$p$范数定义
$$L_p({\mathbf{x}}_i,{\mathbf{x}}_j)={\left(\sum _{l=1}^n|x_i^l-x_j^l{|}^p\right)}^{\frac{1}{p}}$$

当$p=1$时，称为曼哈顿距离；当$p=2$时，称为 欧式距离。由不同的度量方式所确定的最近邻点可能不同。

选择k值

k的选择反映了训练误差（近似误差）与测试误差（估计误差）的权衡，即：

• 若 k取较小值（模型复杂），预测实例较依赖于近邻样本，样本整体利用率低，模型对噪声数据敏感，且可能出现训练误差小（过拟合）、测试误差大的情况；
• 若 k值较大（模型简单），预测实例可利用较多的样本信息，模型抗干扰性强，但计算复杂，且可能出现训练误差大（欠拟合）、测试误差小的情况。

实际运用中，一般通过 交叉验证选取较小的最优k值。

分类决策

给定实例$\mathbf{x}\in \mathcal{X}$，其最近邻的$k$个样本构成集合$N_k(\mathbf{x})$，若$N_k$区域的类别是$c_j$，损失函数使用0/1损失函数$I$，则误分类率
$$\frac{1}{k}\sum _{{\mathbf{x}}_i\in N_k(\mathbf{x})}I(y_i̸=c)$$

最小化误分类率，等价于最小化经验风险$\sum _{{\mathbf{x}}_i\in N_k(\mathbf{x})}I(y_i̸=c)$，故 多数表决规则等价于经验风险最小化。

k近邻评价

当不同类别的样本容量不一致时，模型倾向于样本容量大的类别，可通过将类别附加权值改进模型；
占用存储空间，计算量大（可优化改进，如kd树存储结构）；

2、优化搜索之kd树

什么是kd树？

实现KNN算法时，主要考虑的问题是如何在训练样本集中快速k近邻搜索。最简单的想法是，使用线性扫描的方式，即计算所有样本点与输入实例的距离，再取k个距离最小的点作为k近邻点。当训练集很大时，这种方法计算非常耗时。另一种想法是，构建数据索引，即通过构建树对输入空间进行划分，kd树就是此种实现。

kd树（k-dimension tree，k是指特征向量的维数），是一种存储k维空间中数据的平衡二叉树型结构，主要用于 范围搜索和最近邻搜索。kd树实质是一种空间划分树，其每个节点对应一个k维的点，每个非叶节点相当于一个分割超平面，将其所在区域划分为两个子区域。

kd树的结构可使得每次在局部空间中搜索目标数据，减少了不必要的数据搜索，从而加快了搜索速度。

如何构建kd树？

构建kd树的过程，是不断地选择垂直于坐标轴（切分轴）的超平面将样本集所在的k维空间二分，生成一系列不重叠的k维超矩形区域。

选择切分轴
有多种方法可以选择切分轴超平面，如随着树的深度轮流选择各轴、每次选择数值方差最大的轴等。

选择切分点
一般使用中位数作为切分点，可保证切分后得到的左右子树深度差不超过1，所得二叉树为平衡二叉树。

构建过程
输入数据集 T = { x 1 , ⋯   , x N } T = \{\bm x_1, \cdots, \bm x_N\} T={x1​,⋯,xN​}，其中${\mathbf{x}}_i=(x_i^1,\cdots ,x_i^k)$，具体步骤如下：

• 构建根节点，根节点对应于包含$T$的k维空间的超矩形区域。选取$x^1$为切分轴、$T$中所有点$x^1$坐标的中位数为切分点，使用过切分点且与垂直于切分轴的超平面，将根节点对应的超矩形区域切分为两个子区域，并对应于其左右子节点。其中，左节点区域各点的$x^1$坐标不大于切分点，右节点区域各点的$x^1$坐标大小于切分点，并将切分点保存在根节点。

• 对子节点重复步骤$I$，即对于深度为$j$的节点$j_i$，选择$x^l$为切分轴、$j_i$包含的区域中所有点$x^l$坐标的中位数为切分点，其中$l=(j+1)\mathrm{m}\mathrm{o}\mathrm{d}k$，将$j_i$对应的区域划分为两个子区域，并对应其左右子节点，直至两个子区域没有实例为止。

对于二维空间中的数据集， T = { ( 2 , 3 ) , ( 5 , 4 ) , ( 9 , 6 ) , ( 4 , 7 ) , ( 8 , 1 ) , ( 7 , 2 ) } T=\{(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)\} T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}，形成的kd树如下：

    图2 超矩形划分（左）与数据存储结构（右）

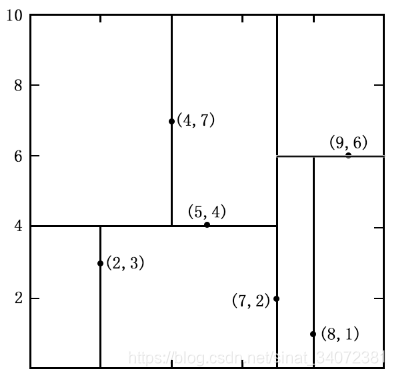
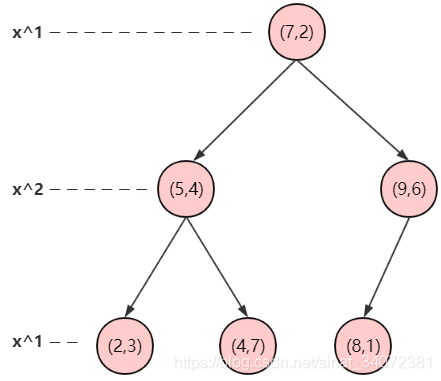
如何在kd树中搜索输入实例的k近邻？

利用kd树搜索最近邻样本，可省去对大部分数据的搜索，从而减少计算量。当数据随机分布时，搜索最近邻的时间复杂度为$O(\log N)$，$N$为样本集容量，当空间维数接近$N$时，效率迅速下降。如下图3为搜索过程动态效果图。

图3 k近邻搜索动态效果

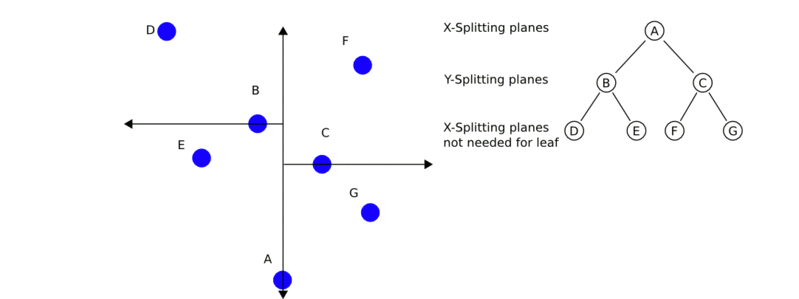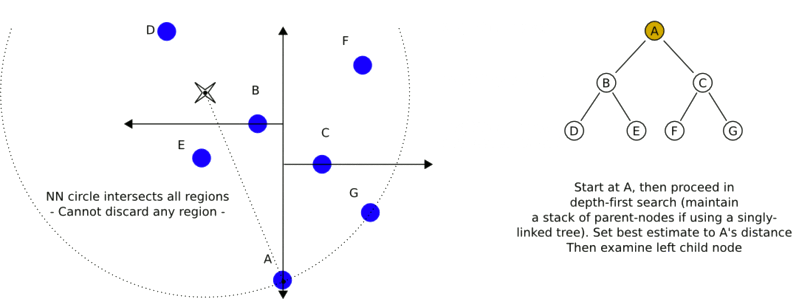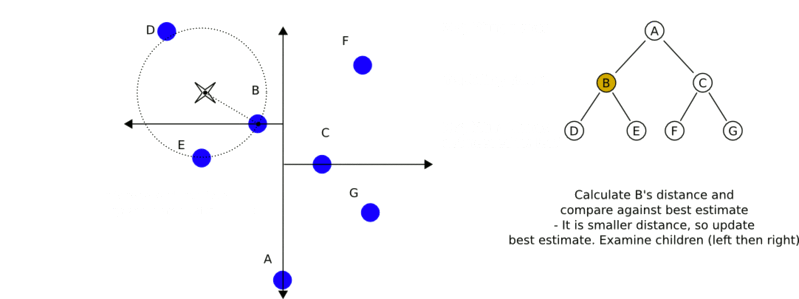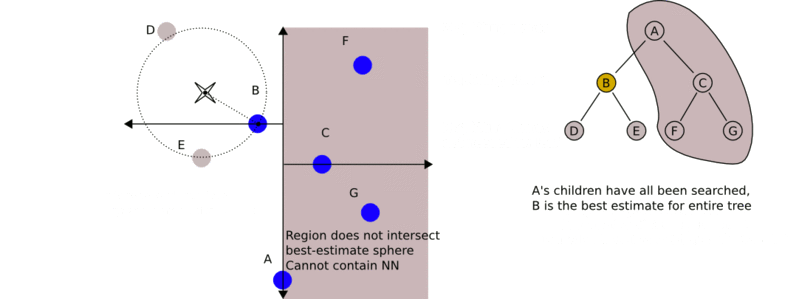
最近邻搜索
给定一个输入实例，首先找到包含输入实例的叶节点。然后从该叶节点出发，依次回退到父节点。不断查找与输入实例最近邻的节点，当不存在距离更小的节点时终止搜索《统计学习方法》。
输入实例与其最近邻样本点形成的超球体的内部一定没有其他样本点。 基于这种性质，最近邻搜索算法如下：

1. 从根节点出发，找到包含输入实例的叶节点，即若输入实例当前维的坐标小于切分点的坐标，移动到左子节点，否则移动到右子节点，直到到达叶节点未知，并将当前叶节点作为“当前最近点”；
2. 递归地向上回退，对每个节点执行以下操作：
   a. 若该节点保存的实例比"当前最近点"距离输入实例更近，则将该实例作为“当前最近点”；
   b. “当前最近点”一定存在于该节点一个子节点对应的区域，检查该子节点的兄弟节点对应区域是否有更近的点。即若“当前最近点”与输入实例形成的超球体与"当前最近点"的父节点的分割超平面相交，则"当前最近点"的兄弟节点可能含有更近的点，此时将该兄弟节点作为根节点一样，执行步骤1。若不相交，则向上回退。
3. 当回退到根节点时，搜索结束。最后的“当前最近点”，即为输入实例的最近邻点。

k近邻搜索
《统计学习方法》中未介绍k近邻的搜索算法，通过查找其它资料，整理了算法实现思想。
最近邻的搜索算法是首先找到叶节点，再依次向上回退，直至到达根节点。本文章中的k近邻的搜索算法与其相反，是从根节点开始依次向下查找，直至到达叶节点。算法实现如下：

• 首先构建空的最大堆（列表），从根节点出发，计算当前节点与输入实例的距离，若最大堆元素小于k个，则将距离插入最大堆中，否则比较该距离是否小于堆顶距离值，若小于，则使用该距离替换堆顶元素；
• 递归的遍历kd树中的节点，通过如下方式控制进入分支：
  • 若堆中元素小于k个或该节点中的样本点与输入实例形成的超球体包含堆顶样本点，则进入左右子节点搜索；
  • 否则，若输入实例当前维的坐标小于该节点当前维的坐标，则进入左子节点搜索；
  • 否则，进入右子节点搜索；
• 当到达叶节点时，搜索结束。最后最大堆中的k个节点，即为输入实例的k近邻点。

3、python实现KD树、KNN算法

代码实现

# -*- coding: utf-8 -*-l
import random
from copy import deepcopy
from time import time

import numpy as np
from numpy.linalg import norm

from collections import Counter

Counter([0, 1, 1, 2, 2, 3, 3, 4, 3, 3]).most_common(1)


def partition_sort(arr, k, key=lambda x: x):
    """
    以枢纽(位置k)为中心将数组划分为两部分, 枢纽左侧的元素不大于枢纽右侧的元素

    :param arr: 待划分数组
    :param p: 枢纽前部元素个数
    :param key: 比较方式
    :return: None
    """
    start, end = 0, len(arr) - 1
    assert 0 <= k <= end
    while True:
        i, j, pivot = start, end, deepcopy(arr[start])
        while i < j:
            # 从右向左查找较小元素
            while i < j and key(pivot) <= key(arr[j]):
                j -= 1
            if i == j: break
            arr[i] = arr[j]
            i += 1
            # 从左向右查找较大元素
            while i < j and key(arr[i]) <= key(pivot):
                i += 1
            if i == j: break
            arr[j] = arr[i]
            j -= 1
        arr[i] = pivot

        if i == k:
            return
        elif i < k:
            start = i + 1
        else:
            end = i - 1


def max_heapreplace(heap, new_node, key=lambda x: x[1]):
    """
    大根堆替换堆顶元素

    :param heap: 大根堆/列表
    :param new_node: 新节点
    :return: None
    """
    heap[0] = new_node
    root, child = 0, 1
    end = len(heap) - 1
    while child <= end:
        if child < end and key(heap[child]) < key(heap[child + 1]):
            child += 1
        if key(heap[child]) <= key(new_node):
            break
        heap[root] = heap[child]
        root, child = child, 2 * child + 1
    heap[root] = new_node


def max_heappush(heap, new_node, key=lambda x: x[1]):
    """
    大根堆插入元素

    :param heap: 大根堆/列表
    :param new_node: 新节点
    :return: None
    """
    heap.append(new_node)
    pos = len(heap) - 1
    while 0 < pos:
        parent_pos = pos - 1 >> 1
        if key(new_node) <= key(heap[parent_pos]):
            break
        heap[pos] = heap[parent_pos]
        pos = parent_pos
    heap[pos] = new_node


class KDNode(object):
    """kd树节点"""

    def __init__(self, data=None, label=None, left=None, right=None, axis=None, parent=None):
        """
        构造函数

        :param data: 数据
        :param label: 数据标签
        :param left: 左孩子节点
        :param right: 右孩子节点
        :param axis: 分割轴
        :param parent: 父节点
        """
        self.data = data
        self.label = label
        self.left = left
        self.right = right
        self.axis = axis
        self.parent = parent


class KDTree(object):
    """kd树"""

    def __init__(self, X, y=None):
        """
        构造函数

        :param X: 输入特征集, n_samples*n_features
        :param y: 输入标签集, 1*n_samples
        """
        self.root = None
        self.y_valid = False if y is None else True
        self.create(X, y)

    def create(self, X, y=None):
        """
        构建kd树

        :param X: 输入特征集, n_samples*n_features
        :param y: 输入标签集, 1*n_samples
        :return: KDNode
        """

        def create_(X, axis, parent=None):
            """
            递归生成kd树

            :param X: 合并标签后输入集
            :param axis: 切分轴
            :param parent: 父节点
            :return: KDNode
            """
            n_samples = np.shape(X)[0]
            if n_samples == 0:
                return None
            mid = n_samples >> 1
            partition_sort(X, mid, key=lambda x: x[axis])

            if self.y_valid:
                kd_node = KDNode(X[mid][:-1], X[mid][-1], axis=axis, parent=parent)
            else:
                kd_node = KDNode(X[mid], axis=axis, parent=parent)

            next_axis = (axis + 1) % k_dimensions
            kd_node.left = create_(X[:mid], next_axis, kd_node)
            kd_node.right = create_(X[mid + 1:], next_axis, kd_node)
            return kd_node

        print('building kd-tree...')
        k_dimensions = np.shape(X)[1]
        if y is not None:
            X = np.hstack((np.array(X), np.array([y]).T)).tolist()
        self.root = create_(X, 0)

    def search_knn(self, point, k, dist=None):
        """
        kd树中搜索k个最近邻样本

        :param point: 样本点
        :param k: 近邻数
        :param dist: 度量方式
        :return:
        """

        def search_knn_(kd_node):
            """
            搜索k近邻节点

            :param kd_node: KDNode
            :return: None
            """
            if kd_node is None:
                return
            data = kd_node.data
            distance = p_dist(data)
            if len(heap) < k:
                # 向大根堆中插入新元素
                max_heappush(heap, (kd_node, distance))
            elif distance < heap[0][1]:
                # 替换大根堆堆顶元素
                max_heapreplace(heap, (kd_node, distance))

            axis = kd_node.axis
            if abs(point[axis] - data[axis]) < heap[0][1] or len(heap) < k:
                # 当前最小超球体与分割超平面相交或堆中元素少于k个
                search_knn_(kd_node.left)
                search_knn_(kd_node.right)
            elif point[axis] < data[axis]:
                search_knn_(kd_node.left)
            else:
                search_knn_(kd_node.right)

        if self.root is None:
            raise Exception('kd-tree must be not null.')
        if k < 1:
            raise ValueError("k must be greater than 0.")

        # 默认使用2范数度量距离
        if dist is None:
            p_dist = lambda x: norm(np.array(x) - np.array(point))
        else:
            p_dist = lambda x: dist(x, point)

        heap = []
        search_knn_(self.root)
        return sorted(heap, key=lambda x: x[1])

    def search_nn(self, point, dist=None):
        """
        搜索point在样本集中的最近邻

        :param point:
        :param dist:
        :return:
        """
        return self.search_knn(point, 1, dist)[0]

    def pre_order(self, root=KDNode()):
        """先序遍历"""
        if root is None:
            return
        elif root.data is None:
            root = self.root

        yield root
        for x in self.pre_order(root.left):
            yield x
        for x in self.pre_order(root.right):
            yield x

    def lev_order(self, root=KDNode(), queue=None):
        """层次遍历"""
        if root is None:
            return
        elif root.data is None:
            root = self.root

        if queue is None:
            queue = []

        yield root
        if root.left:
            queue.append(root.left)
        if root.right:
            queue.append(root.right)
        if queue:
            for x in self.lev_order(queue.pop(0), queue):
                yield x

    @classmethod
    def height(cls, root):
        """kd-tree深度"""
        if root is None:
            return 0
        else:
            return max(cls.height(root.left), cls.height(root.right)) + 1


class KNeighborsClassifier(object):
    """K近邻分类器"""

    def __init__(self, k, dist=None):
        """构造函数"""
        self.k = k
        self.dist = dist
        self.kd_tree = None

    def fit(self, X, y):
        """建立kd树"""
        print('fitting...')
        X = self._data_processing(X)
        self.kd_tree = KDTree(X, y)

    def predict(self, X):
        """预测类别"""
        if self.kd_tree is None:
            raise TypeError('Classifier must be fitted before predict!')
        search_knn = lambda x: self.kd_tree.search_knn(point=x, k=self.k, dist=self.dist)
        y_ptd = []
        X = (X - self.x_min) / (self.x_max - self.x_min)
        for x in X:
            y = Counter(r[0].label for r in search_knn(x)).most_common(1)[0][0]
            y_ptd.append(y)
        return y_ptd

    def score(self, X, y):
        """预测正确率"""
        y_ptd = self.predict(X)
        correct_nums = len(np.where(np.array(y_ptd) == np.array(y))[0])
        return correct_nums / len(y)

    def _data_processing(self, X):
        """数据归一化"""
        X = np.array(X)
        self.x_min = np.min(X, axis=0)
        self.x_max = np.max(X, axis=0)
        X = (X - self.x_min) / (self.x_max - self.x_min)
        return X

代码测试

if __name__ == '__main__':
    """测试程序正确性
    使用kd-tree和计算全部距离, 比对两种结果是否一致"""
    N = 100000
    X = [[np.random.random() * 100 for _ in range(3)] for _ in range(N)]
    kd_tree = KDTree(X)

    for x in X[:10]:
        res1 = ([list(node[0].data) for node in kd_tree.search_knn(x, 20)])
        distances = norm(np.array(X) - np.array(x), axis=1)
        res2 = ([list(X[i]) for _, i in sorted(zip(distances, range(N)))[:20]])
        if all(x in res2 for x in res1):
            print('correct ^_^ ^_^')
        else:
            print('error >_< >_<')
    print('\n')

    """10万个样本集中查找10个实例的最近邻"""
    n = 10
    indices = random.sample(range(N), n)
    # 1、kd-tree搜索, 0.19251227378845215s
    tm = time()
    for i, index in enumerate(indices):
        kd_tree.search_nn(X[index])
    print('kd-tree search: {}s'.format(time() - tm))

    # 2、numpy计算全部样本与新实例的距离, 0.5163719654083252s
    tm = time()
    for i, index in enumerate(indices):
        min(norm(X - np.array(X[index]), axis=0))
    print('numpy search: {}s'.format(time() - tm))

    # 3、python循环计算距离, 7.144993782043457s
    tm = time()
    for i, index in enumerate(indices):
        min([norm(np.array(X[index]) - np.array(x)) for x in X])
    print('python search: {}s'.format(time() - tm))
    print('\n\n')

if __name__ == '__main__':
    """模型测试"""
    X, y = [], []
    with open(r"C:\Users\MERLIN\Desktop\knn_dataset.txt") as f:
        for line in f:
            tmp = line.strip().split('\t')
            X.append(tmp[:-1])
            y.append(tmp[-1])
    X = np.array(X, dtype=np.float64)
    y = np.array(y, dtype=np.float64)

    """训练误差"""
    knc = KNeighborsClassifier(10)
    knc.fit(X, y)
    print(knc.score(X, y))  # 0.963
    print('\n')

    """测试误差"""
    X_train, X_test = X[:980], X[-20:]
    y_train, y_test = y[:980], y[-20:]
    knc = KNeighborsClassifier(10)
    knc.fit(X_train, y_train)
    print(knc.score(X_test, y_test))  # 1.0

《机器学习实战》约会数据集：链接：https://pan.baidu.com/s/1RNW3S0gqlIvancWP-6yqAQ 提取码：8htf

测试结果

C:\ProgramData\Anaconda3\python.exe C:/Users/MERLIN/Desktop/Python/knn.py
building kd-tree...
correct ^_^ ^_^
correct ^_^ ^_^
correct ^_^ ^_^
correct ^_^ ^_^
correct ^_^ ^_^
correct ^_^ ^_^
correct ^_^ ^_^
correct ^_^ ^_^
correct ^_^ ^_^
correct ^_^ ^_^


kd-tree search: 0.1874983310699463s
numpy search: 0.6091194152832031s
python search: 6.774036645889282s

fitting...
building kd-tree...
0.963

fitting...
building kd-tree...
1.0

Process finished with exit code 0