环形队列实现原理

最新推荐文章于 2024-05-13 00:44:27 发布
最新推荐文章于 2024-05-13 00:44:27 发布
阅读量4.1w 收藏 134
点赞数 26
分类专栏： Linux系统开发 文章标签： 数据结构 struct 测试 算法 编程 网络
环形队列是在实际编程极为有用的数据结构,它有如下特点。
   它是一个首尾相连的FIFO的数据结构，采用数组的线性空间,数据组织简单。能很快知道队列是否满为空。能以很快速度的来存取数据。
   因为有简单高效的原因，甚至在硬件都实现了环形队列.
 
   环形队列广泛用于网络数据收发，和不同程序间数据交换（比如内核与应用程序大量交换数据,从硬件接收大量数据）均使用了环形队列.
 
一.环形队列实现原理
------------------------------------------------------------
 
  内存上没有环形的结构，因此环形队列实上是数组的线性空间来实现。那当数据到了尾部如何处理呢？它将转回到0位置来处理。这个的转回是通过取模操作来执行的。
   因此环列队列的是逻辑上将数组元素q[0]与q[MAXN-1]连接，形成一个存放队列的环形空间。
   为了方便读写，还要用数组下标来指明队列的读写位置。head/tail.其中head指向可以读的位置，tail指向可以写的位置。
 
 
 
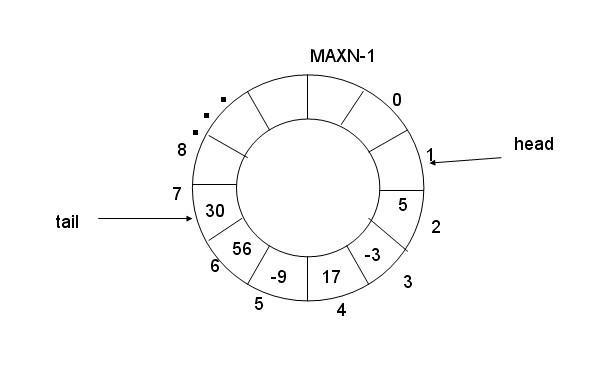
 环形队列的关键是判断队列为空，还是为满。当tail追上head时，队列为满时，当head追上tail时，队列为空。但如何知道谁追上谁。还需要一些辅助的手段来判断.
 
   如何判断环形队列为空，为满有两种判断方法。
   一.是附加一个标志位tag
      当head赶上tail，队列空，则令tag=0,
      当tail赶上head，队列满，则令tag=1,
 
   二.限制tail赶上head，即队尾结点与队首结点之间至少留有一个元素的空间。
      队列空：   head==tail
      队列满：   (tail+1)% MAXN ==head
 
 
 
二.附加标志实现算法
-------------------------------------------------------------
 
  采用第一个环形队列有如下结构 
typedef struct ringq{
   int head; /* 头部，出队列方向*/
   int tail; /* 尾部，入队列方向*/ 
   int tag ;
   int size ; /* 队列总尺寸 */
   int space[RINGQ_MAX]; /* 队列空间 */
  
}RINGQ;

初始化状态:  q->head = q->tail = q->tag = 0;
队列为空:( q->head == q->tail) && (q->tag == 0)
队列为满 : ((q->head == q->tail) && (q->tag == 1))
入队操作:如队列不满，则写入
     q->tail =  (q->tail + 1) % q->size ;
出队操作：如果队列不空，则从head处读出。
    下一个可读的位置在  q->head =  (q->head + 1) % q->size
 
完整代码
    头文件ringq.h 
#ifndef __RINGQ_H__
#define __RINGQ_H__

#ifdef __cplusplus
extern "C" {
#endif 

#define QUEUE_MAX 20

typedef struct ringq{
   int head; /* 头部，出队列方向*/
   int tail; /* 尾部，入队列方向*/ 
   int tag ; /* 为空还是为满的标志位*/
    int size ; /* 队列总尺寸 */
   int space[QUEUE_MAX]; /* 队列空间 */
}RINGQ;

/* 
  第一种设计方法:
     当head == tail 时，tag = 0 为空，等于 = 1 为满。
*/

extern int ringq_init(RINGQ * p_queue);

extern int ringq_free(RINGQ * p_queue);


/* 加入数据到队列 */
extern int ringq_push(RINGQ * p_queue,int data);

/* 从队列取数据 */
extern int ringq_poll(RINGQ * p_queue,int *p_data);


#define ringq_is_empty(q) ( (q->head == q->tail) && (q->tag == 0))

#define ringq_is_full(q) ( (q->head == q->tail) && (q->tag == 1))

#define print_ringq(q) printf("ring head %d,tail %d,tag %d\n", q->head,q->tail,q->tag);
#ifdef __cplusplus
}
#endif 

#endif /* __RINGQ_H__ */


实现代码 ringq.c
  
#include <stdio.h>
#include "ringq.h"

int ringq_init(RINGQ * p_queue)
{
   p_queue->size = QUEUE_MAX ;
   
   p_queue->head = 0;
   p_queue->tail = 0;
   
   p_queue->tag = 0;
   
   return 0;
}

int ringq_free(RINGQ * p_queue)
{
  return 0;
}


int ringq_push(RINGQ * p_queue,int data)
{
  print_ringq(p_queue);
  
  if(ringq_is_full(p_queue))
   {
     
     printf("ringq is full\n");
     return -1;
   }
      
   p_queue->space[p_queue->tail] = data;
   
   p_queue->tail = (p_queue->tail + 1) % p_queue->size ;
   
   /* 这个时候一定队列满了*/
   if(p_queue->tail == p_queue->head)
    {
       p_queue->tag = 1;
    }

    return p_queue->tag ;  
}

int ringq_poll(RINGQ * p_queue,int * p_data)
{
   print_ringq(p_queue);
  if(ringq_is_empty(p_queue))
   {
      
      printf("ringq is empty\n");
     return -1;
   }
   
   *p_data = p_queue->space[p_queue->head];
   
   p_queue->head = (p_queue->head + 1) % p_queue->size ;
   
    /* 这个时候一定队列空了*/
   if(p_queue->tail == p_queue->head)
    {
       p_queue->tag = 0;
    }    
    return p_queue->tag ;
}


测试代码 
/* 测试第一种环形队列*/
void test5()
{
  RINGQ rq, * p_queue;
  int i,data;
  
  p_queue = &rq;
  
  ringq_init(p_queue);
  
  for(i=0; i < QUEUE_MAX +2 ; i++)
  {
   
   ringq_push(p_queue,i+1); 
  } 
    
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  ringq_free(p_queue);
}

/* 测试第一种环形队列,更加复杂的情况*/
void test6()
{
  RINGQ rq, * p_queue;
  int i,data;
  
  p_queue = &rq;
  
  ringq_init(p_queue);
  
  
   ringq_push(p_queue,1); 
   
   ringq_push(p_queue,2); 
  
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
    
  ringq_push(p_queue,3); 
  
  ringq_push(p_queue,4); 
  
  ringq_push(p_queue,5); 
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
       
   ringq_push(p_queue,6); 
     
   if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
     
     if(ringq_poll(p_queue,&data)>=0)
     PRINT_INT(data);
  
  ringq_free(p_queue);
}


 
三.预留空间环境队列
 
 -------------------------------------------------------------------
 
不采用tag,只留一个空间
  
 
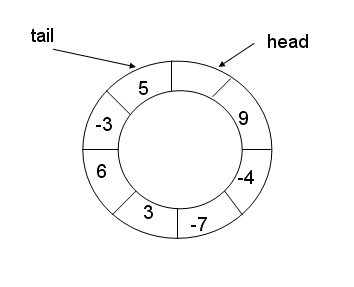
初始化状态:  q->head = q->tail = q->tag = 0;
队列为空:( q->head == q->tail)
队列为满 : (((q->tail+1)%q->size) == q->head )
入队操作:如队列不满，则写入
     q->tail =  (q->tail + 1) % q->size ;
出队操作：如果队列不空，则从head处读出。
    下一个可读的位置在  q->head =  (q->head + 1) % q->size
 
头文件
  ringq.h
    
#ifndef __RINGQ_H__
#define __RINGQ_H__

#ifdef __cplusplus
extern "C" {
#endif 

#define RINGQ_MAX 20

typedef struct ringq{
   int head; /* 头部，出队列方向*/
   int tail; /* 尾部，入队列方向*/ 
   int size ; /* 队列总尺寸 */
   int space[RINGQ_MAX]; /* 队列空间 */
}RINGQ;

/*
  取消tag .限制读与写之间至少要留一个空间
  队列空 head == tail .
  队列满是 (tail+1)%MAX == head  
  初始化是head = tail = 0;   
*/

extern int ringq_init(RINGQ * p_ringq);

extern int ringq_free(RINGQ * p_ringq);

extern int ringq_push(RINGQ * p_ringq,int data);

extern int ringq_poll(RINGQ * p_ringq,int * p_data);

#define ringq_is_empty(q) (q->head == q->tail)

#define ringq_is_full(q) (((q->tail+1)%q->size) == q->head )

#define print_ringq2(q,d) printf("ring head %d,tail %d,data %d\n", q->head,q->tail,d);

#ifdef __cplusplus
}
#endif 

#endif /* __QUEUE_H__ */

 

实现代码ringq.c

#include <stdio.h>

#include "ringq.h"

int ringq_init(RINGQ * p_ringq)
{
  p_ringq->size = RINGQ_MAX;
  
  p_ringq->head = 0;
  p_ringq->tail = 0;
  
  return p_ringq->size;
}

int ringq_free(RINGQ * p_ringq)
{
  return 0;
}

/* 往队列加入数据 */
int ringq_push(RINGQ * p_ringq,int data)
{
   print_ringq(p_ringq,data);
   
   if(ringq_is_full(p_ringq))
     {
         printf("ringq is full,data %d\n",data);
           return -1;
     }
         
   p_ringq->space[p_ringq->tail] = data;
   
   p_ringq->tail = (p_ringq->tail + 1) % p_ringq->size ;   
    
    return p_ringq->tail ;
}


int ringq_poll(RINGQ * p_ringq,int * p_data)
{
   print_ringq(p_ringq,-1);
  if(ringq_is_empty(p_ringq))
   {
     printf("ringq is empty\n");
     return -1;
   }
   
   *p_data = p_ringq->space[p_ringq->head];
   
   p_ringq->head = (p_ringq->head + 1) % p_ringq->size ;
   
   return p_ringq->head;
}

作者： Andrew Huang bluedrum@163.com

kfree1024
关注
  • 26
    点赞
  • 踩
  • 134
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
详解环形队列
m0_61704320的博客
10-27 559
环形队列是一种特殊的队列数据结构，它可以通过循环利用数组中的空间来实现队列的操作。与普通的队列不同，环形队列的队尾指针可以超过数组的末尾，指向数组的开头，形成一个环状结构。一个固定大小的数组，用于存储队列中的元素。一个队头指针，指向队列中的第一个元素。一个队尾指针，指向队列中最后一个元素的下一个位置。队列为空时，队头指针和队尾指针相等。当向队列中添加元素时，队尾指针向后移动，并将元素放入队尾指针指向的位置。当从队列中删除元素时，队头指针向后移动，并返回队头指针指向的元素。
[缓存] RingBuff 环形队列、环形缓冲区及有锁无锁实现
小田的专栏
02-20 1390
由于自旋锁不需要进行线程切换，所以它完全在用户态下实现，加锁开销低，但是由于其采用忙等待的策略，对于短期加锁来说没问题，但是长期锁定的时候就会导致CPU资源的大量消耗。如果读取数据的速度跟不上写入数据的速度，旧的数据将被新写入的数据覆盖。所以当互斥锁加锁失败的时候，就伴随着两次上下文切换的开销，而如果我们锁定的时间较短，可能上下文切换的时间会比锁定的时间还要长。由于自旋锁和互斥锁的失败策略不同，自旋锁采用忙等待的策略，而互斥锁采用线程切换的策略，由于策略不同，它们的应用场景也不同。
2024年C C++最全【C C++开源库】环形队列，消息队列库_开源 queue 库，C C++并发原理解析
最新发布
2401_84978603的博客
05-13 914
环形队列的关键是判断队列为空，还是为满。当head追上tail时，队列为空。为了方便读写，还要用数组下标来指明队列的读写位置。head/tail.其中head指向可以读的位置，tail指向可以写的位置。内存上没有环形的结构，因此环形队列实上是数组的线性空间来实现。“环形队列”和“消息队列”在嵌入式领域有应用非常广泛，相信有经验的嵌入式软件工程师对它们都不陌生。但经常看到一些初学者问一些相关的问题，今天就来分享一下关于“环形队列”和“消息队列”的内容。出队操作，如果队列不空，则从head处读出。
环形队列详解
qq_54938554的博客
10-25 1837
队列是一种线性数据结构，它遵循先进先出或后近后出的原则。队列允许在一端插入元素，另一端删除元素。队列有时也被称为待办事项列表，尤其是在计算机程序中，它被广泛用于任务排队、缓存和异步处理方案中。环形队列，它可以在固定大小的数组中循环使用。它类似于普通队列，但与普通队列不同的是，在环形队列中，队列的队尾可以接到数组的开头，使数组像一个圆环一样循环。因此，环形队列往往比普通队列的效率更高，尤其是在实现循环缓冲区等应用时。环形队列主要的操作有入队和出队。int front;int rear;
【数据结构(C语言描述)】环形队列
xiyang_DING
02-17 4120
环形队列的数组和链表实现以及对应的接口
数据结构--环形队列的介绍与实现
热门推荐
凌云
06-04 1万+
数据结构--环形队列实现一、环形队列实现原理环形队列的几个判断条件二、代码实现1.环形队列类（CircleQueue）2.环形队列类测试类3.程序运行结果4.完整代码 环形队列可以用数组实现，也可以使用循环链表实现.在使用数组实现循环队列的时候，需要理解清楚队列头和队列尾的判断空还是满的处理方法； 环形队列特点： 避免假溢出现象（由于入队和出队的操作，头尾指针只增加不减少，致使被删元素的空间永远无法重新利用，当队列继续存储元素时，出现尾指针已经到达了队列尾，而实际头指针前面并未满的情况），可以将队列空间充
环形队列的原理以及实现
猛犸象
07-15 1630
环形队列的原理以及实现
数据结构—循环队列（环形队列）
AI_ELF的博客
08-26 3547
循环队列选择用数组实现，循环队列需要用一个指针来指向存储队列数据的空间，用两个变量来记录队列中存储数据的起始（对头）和末尾（队尾）的数组位置，最后用一个变量记录队列的存储数据的最大容量。
数据结构与算法之环形队列
【原】编程界的小学生
12-16 1075
一、 二、 三、
c++实现的无锁环形队列
11-05
1. c++实现的无锁环形队列，注释详细，讲解了环形队列的实现原理和操作技巧 2. 在linux服务器下，可以自己编译，运行，也可以修改参数后做测试 3. 编译的命令如下：g++ -std=c++11 -o test main.cpp ring_buffer.cpp...
C#环形队列的实现方法详解
01-20
一、环形队列是什么 队列是一种常用的数据结构，这种结构保证了数据是按照“先进先出”的原则进行操作的，即最先进去的元素也是最先出来的元素.环形队列是一种特殊的队列结构，保证了元素也是先进先出的，但与一般...
java版实现环形队列
10-18
java实现的队列，通过图的方式来演示环形队列的结构和原理，通过图从感官上了解队列的形式，从逻辑上更好的明白环形队列的实质。
Java 队列实现原理及简单实现代码
09-01
【Java 队列实现原理】 队列是一种重要的数据结构，其主要特点是先进先出（First In First Out，简称FIFO）。在Java中，队列主要用于处理数据的有序入列和出列，常用于任务调度、多线程通信、网络数据包处理等领域...
基于stm32串口的环形队列应用
12-18
在提供的"RingBufffer"文件中，包含了具体的环形队列实现代码，这部分代码应该包含了上述提到的各个关键点。通过阅读和理解这些代码，开发者可以了解到如何在实际项目中应用和自定义环形队列，以便满足不同场景的...
C语言数据结构——环形队列
weixin_44343938的博客
12-11 1785
其次，假设capacity为4，那实际数组空间为5，下标为0,1,2,3,4，当rear==4，此时下标0,1,2,3中都有数据，rear的理论最大值为rear+1 == 5，要使rear+1 == 5 == 0就需要使5%5，如此%的右边就为rear的理论最大值，front同理。如果一个可放入n个数据的环形队列的capacity为n的话，一开始front == rear == 0，假设不入队一直出队，当队满时rear又循环到了0下标，此时front == rear == 0仍成立。
C程序设计：环形队列
weixin_42549534的博客
06-28 491
2.环形队列读的速度慢于写时，一旦写的地址到达了读的地址时，队列将被清空。1.在多线程的队列读写，应在读写时加锁来保护。
C++实现环形队列
静水流深
10-29 3116
实现环形队列 线性队列原理图： 假设是长度为5的数组，初始状态，空队列如所示，front与 rear指针均指向下标为0的位置。然后入队a1、a2、a3、a4， front指针依然指向下标为0位置，而rear指针指向下标为4的位置。 出队a1、a2，则front指针指向下标为2的位置，rear不变，如下图所示，再入队a5，此时front指针不变，rear指针移动到数组之外 ，造成假溢出的现象： 为了解决这个问题，引入了循环队列的概念。 循环队列原理图： 可以看到当循环队列属于上图的d1情况时，是无法判断
c++实现环形队列
weixin_40428368的博客
06-09 981
环形队列相对于普通队列有一定的好处。 头文件的内容如下： #include <stdlib.h> class CircleQueue { public: CircleQueue(); CircleQueue(int capacity); ~CircleQueue(); bool IsEmpty(); bool IsFull(); void ClearQueue(); int Length(); bool EnQueue(int element); bool DeQueue(in
数据结构之环形队列实现 (C++/数组)
07-02 1281
数据结构之环形队列实现 (C++/数组) 1.概念示意图 内存中不存在环形数据结构，均由基础结构实现逻辑上的闭环效果 2.环形队列与普通队列的区别 1.front头部指针 一般队列：front头部指针初始值为-1，从队列取数据时，该值依次递增，指向的元素即待取出的数据，而队列的头部数据所在的指针位置为front+1。当front=maxSize-1时，队列最后一个数据取出，此时队列为空。 环形队列：front头部指针初始值为0，指向的元素既是队列的头部数据也是待取出的数据。从队列取数据时..
c语言环形指针队列原理
05-21
环形指针队列是一种非常常见的数据结构，通常用于解决多任务并发处理、缓存数据等问题。它的核心思想是将队列中的元素存储在一个环形的数组中，通过两个指针front和rear分别指向队头和队尾，实现入队和出队操作。 具体实现原理如下： 1. 定义环形队列结构体，包含队列数组、队头指针front、队尾指针rear、队列长度等信息。 ``` #define MAXSIZE 100 typedef struct { int data[MAXSIZE]; int front; int rear; int size; } CircleQueue; ``` 2. 初始化队列，将队头和队尾指针都指向0。 ``` void InitQueue(CircleQueue *queue) { queue->front = 0; queue->rear = 0; queue->size = 0; } ``` 3. 判断队列是否为空，当队头指针等于队尾指针时，队列为空。 ``` int IsEmpty(CircleQueue *queue) { return queue->front == queue->rear; } ``` 4. 判断队列是否满，当队尾指针加1等于队头指针时，队列满。 ``` int IsFull(CircleQueue *queue) { return (queue->rear + 1) % MAXSIZE == queue->front; } ``` 5. 入队操作，将元素插入队尾，队尾指针加1，当队尾指针等于数组长度时，将其置为0。 ``` void EnQueue(CircleQueue *queue, int x) { if (IsFull(queue)) { printf("Queue is full.\n"); return; } queue->data[queue->rear] = x; queue->rear = (queue->rear + 1) % MAXSIZE; queue->size++; } ``` 6. 出队操作，将队头元素弹出，队头指针加1，当队头指针等于数组长度时，将其置为0。 ``` int DeQueue(CircleQueue *queue) { if (IsEmpty(queue)) { printf("Queue is empty.\n"); return -1; } int x = queue->data[queue->front]; queue->front = (queue->front + 1) % MAXSIZE; queue->size--; return x; } ``` 这样，就完成了环形指针队列的实现。需要注意的是，由于在环形队列中，队尾指针可能会超过数组长度，因此需要使用取模运算将其限制在数组范围内。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值