动手学深度学习-Day3-深度学习基础

PS：最近一堆事儿，进度缓慢

李沐-动手学深度学习-Day3

线性回归实现

读取数据集

//返回batch_size（批量大小）个随机样本的特征和标签。
def data_iter(batch_size, features, labels):
    num_examples = len(features)     #features定义为1000*2,1000个样本，2个特征，len函数输出1000
    indices = list(range(num_examples))
    random.shuffle(indices)  # 样本的读取顺序是随机的
    for i in range(0, num_examples, batch_size):
        j = nd.array(indices[i: min(i + batch_size, num_examples)])
        yield features.take(j), labels.take(j)  # take函数根据索引返回对应元素
//调用函数，返回10组样本
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break

初始化模型参数

对于线性回归模型中的权重参数和偏差进行设置。

w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))  #权重参数是均值0，标差0.01的正态随机数，num_inputs=2
b = nd.zeros(shape=(1,))
//创建梯度
w.attach_grad()
b.attach_grad()

attach_grad()函数：将需要求梯度的参数附加上梯度信息，以便在模型训练过程中进行自动求导和参数更新。模型训练时，就可以自动地计算参数w和b的梯度，并进行参数更新。

定义模型、损失函数、优化算法

1、模型：即线性回归方法

def linreg(X, w, b):  # 函数输入参数为样本特征，权重和偏差
    return nd.dot(X, w) + b  #dot做矩阵乘法

2、损失函数：平方损失函数，reshape函数用于将实际的label变成预测的y_hat的形状。
$$\frac{1}{2}(\hat{y}-y{)}^2$$

def squared_loss(y_hat, y):  # 输入参数为通过线性回归计算式得到的预测值和真实值
   return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2  

3、优化算法：sgd函数，小批量（每轮迭代中随机均匀采样多个样本组成一个小批量）随机梯度下降算法

def sgd(params, lr, batch_size):  # params是模型中的参数，lr是学习率，batch_size是批量的大小
  for param in params:
      param[:] = param - lr * param.grad / batch_size 

训练模型

多次迭代模型参数
backward()函数：计算网络中变量的梯度。根据输出变量构建计算图，并计算每个变量的梯度。计算完成后，可以通过grad属性得到每个变量的梯度值。

lr = 0.03    #学习率
num_epochs = 3   #迭代周期
net = linreg   #模型
loss = squared_loss   #损失函数

for epoch in range(num_epochs):  # 训练模型一共需要num_epochs个迭代周期
  # 在每一个迭代周期中，会使用训练数据集中所有样本一次（假设样本数能够被批量大小整除）。X
  # 和y分别是小批量样本的特征和标签
  for X, y in data_iter(batch_size, features, labels):
      with autograd.record():   #做前向计算，即得到损失函数
          l = loss(net(X, w, b), y)  # l是有关小批量X和y的损失
      l.backward()  # 小批量的损失对模型参数求梯度
      sgd([w, b], lr, batch_size)  # 使用小批量随机梯度下降迭代模型参数，每一轮迭代都会更新参数w和b
  train_l = loss(net(features, w, b), labels)
  print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))

输出结果：
num: 1000
epoch 1, loss 0.054382
num: 1000
epoch 2, loss 0.000248
num: 1000
epoch 3, loss 0.000050
在训练完成后，可以观察迭代更新的参数和真实参数的区别。

true_w, w    #在生成数据集时设定了true_w的数值，用该数值得到labels，即y
true_b, b

输出真实w和训练后的w，两个参数
([2, -3.4],
[[ 1.9996792]
[-3.3996103]]
<NDArray 2x1 @cpu(0)>)
输出真实b和训练后的b
(4.2,
[4.1986103]
<NDArray 1 @cpu(0)>)

softmax回归实现理论过程

模型输出可以是一个离散值，使用softmax做分类，此时的输出单元变成多个。

关于softmax如何实现分类

首先，softmax回归跟线性回归一样将输入特征与权重做线性叠加，但是其输出量的个数是类别数。而线性回归中的输出是一个连续的数。如书中举例，假设有4个特征，可以决定三个类别，则此时的输出与特征之间的关系如下：
$$\begin{array}{rl}{o}_1& =x_1{w}_{11}+x_2{w}_{21}+x_3{w}_{31}+x_4{w}_{41}+b_1,\\ o_2& =x_1{w}_{12}+x_2{w}_{22}+x_3{w}_{32}+x_4{w}_{42}+b_2,\\ o_3& =x_1{w}_{13}+x_2{w}_{23}+x_3{w}_{33}+x_4{w}_{43}+b_3.\end{array}$$
上式即可以看出每一个输出量和特征之间的关系依然是线性叠加。如果用神经网络图表示，可以表示如下：

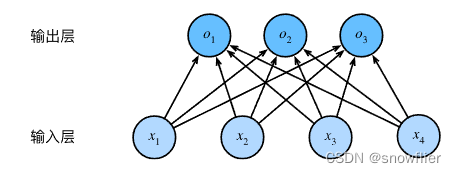
其次，分类问题是需要得到离散的预测输出，上图中的输出o看作是某个类别的置信度，选择最大的即为所预测的类别。但是，线性叠加的输出范围不确定，因此，使用softmax晕眩解决这一问题，通过如下计算，将输出值变换为正且和为1的概率分布，即
$${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3=\text{softmax}(o_1,o_2,o_3),$$

$${\hat{y}}_1=\frac{\exp (o_1)}{{\sum }_{i=1}^3\exp (o_i)},{\hat{y}}_2=\frac{\exp (o_2)}{{\sum }_{i=1}^3\exp (o_i)},{\hat{y}}_3=\frac{\exp (o_3)}{{\sum }_{i=1}^3\exp (o_i)}.$$

显然，${\hat{y}}_1+{\hat{y}}_2+{\hat{y}}_3=1$，且，$0\le {\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3\le 1$
$$\underset{i}{\mathrm{argmax}}{o}_i=\underset{i}{\mathrm{argmax}}{\hat{y}}_i,$$
最后，我们将上述的运算表示成矢量计算的形式。仍然假设有4个特征，3个输出，因此权重和偏差可以表示成如下的矩阵形式
$$\mathbf{W}=\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\\ w_{41}& w_{42}& w_{43}\end{array}\right],\mathbf{b}=\left[\begin{array}{ccc}{b}_1& b_2& b_3\end{array}\right],$$
对第$i$个样本而言，其输入特征表示为
$${\mathbf{x}}^{(i)}=\left[\begin{array}{cccc}{x}_1^{(i)}& x_2^{(i)}& x_3^{(i)}& x_4^{(i)}\end{array}\right],$$
线性加权后的输出表示为
$${\mathbf{o}}^{(i)}=\left[\begin{array}{ccc}{o}_1^{(i)}& o_2^{(i)}& o_3^{(i)}\end{array}\right],$$
经过softmax运算后的预测类别的概率表示为
$${\hat{\mathbf{y}}}^{(i)}=\left[\begin{array}{ccc}{\hat{y}}_1^{(i)}& {\hat{y}}_2^{(i)}& {\hat{y}}_3^{(i)}\end{array}\right].$$
因此，上述对于第$i$个样本分类的矢量计算可以表示为
$$\begin{array}{rl}{\mathbf{o}}^{(i)}& ={\mathbf{x}}^{(i)}\mathbf{W}+\mathbf{b},\\ {\hat{\mathbf{y}}}^{(i)}& =\text{softmax}({\mathbf{o}}^{(i)}).\end{array}$$
当然，我们也可以得到小批量样本分类的矢量计算表达式，假设批量大小为$n$,特征数为$d$,输出的类别数为$q$。
假设，一批样本的特征表示为$\mathbf{X}\in {\mathbb{R}}^{n\times d}$，回归表达式中的权重和偏差表示为$\mathbf{W}\in {\mathbb{R}}^{d\times q}$和$\mathbf{b}\in {\mathbb{R}}^{1\times q}$。则可以得到
$$\begin{array}{rl}\mathbf{O}& =\mathbf{X}\mathbf{W}+\mathbf{b},\\ \hat{\mathbf{Y}}& =\text{softmax}(\mathbf{O}),\end{array}$$

关于交叉熵损失函数

定义为
$$H\left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)=-\sum _{j=1}^q{y}_j^{(i)}\log {\hat{y}}_j^{(i)},$$
假设训练数据集的样本数为$n$，交叉熵损失函数定义为
$$\ell (\mathbf{\Theta })=\frac{1}{n}\sum _{i=1}^{n}H\left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right),$$

softmax回归的实现

关于本书中用到的数据集

这里综合两个文件：
chapter_deep-learning-basics/fashion-mnist.ipynb，—专门讲这个数据集
chapter_deep-learning-basics/softmax-regression-scratch.ipynb ----上面的数据集实际已经封装到了load_data_fashion_mnist函数中，可以直接调用读取数据集。
1、获取数据集
导入必要的包及模块

%matplotlib inline
import d2lzh as d2l
from mxnet.gluon import data as gdata  --gluon提供了data包来读取数据，将导入的data模块用gdata代替
import sys
import time 
//获取训练数据和测试数据
mnist_train = gdata.vision.FashionMNIST(train=True)   ---参数train
mnist_test = gdata.vision.FashionMNIST(train=False)
//训练集样本60000，测试集10000，共10个类别，每个类别是6000和1000
len(mnist_train), len(mnist_test)

导入后的结果

// 通过[]访问任何一个样本
feature, label = mnist_train[0]   --获取第一个训练样本的图像及标签
//feature表征图像，示例是一个28像素的图像，像素数值是0-255之间的数表示，灰度图像，则通道数为1
feature.shape, feature.dtype

得到结果为((28, 28, 1), numpy.uint8)
图像的类别是用文本表示的，还需要有数字标签。

# 本函数已保存在d2lzh包中方便以后使用
def get_fashion_mnist_labels(labels):
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]
//下面定义的是可以在一行中画出多个图像和对应标签的函数
def show_fashion_mnist(images, labels):   #输入参数是图像及标签
    d2l.use_svg_display()
    # 这里的_表示我们忽略（不使用）的变量
    _, figs = d2l.plt.subplots(1, len(images), figsize=(12, 12))    #画子图的方式
    for f, img, lbl in zip(figs, images, labels):
        f.imshow(img.reshape((28, 28)).asnumpy())
        f.set_title(lbl)
        f.axes.get_xaxis().set_visible(False)
        f.axes.get_yaxis().set_visible(False)
X, y = mnist_train[0:9]   #取前9个样本的图像和标签
show_fashion_mnist(X, get_fashion_mnist_labels(y))    #调用显示函数画出图

2、利用封装好的函数读取数据集
在d2lzh.load_data_fashion_mnist函数中直接获取数据集，返回train_iter和test_iter两个变量。

%matplotlib inline
import d2lzh as d2l
from mxnet import autograd, nd
//读数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)    ---这个函数内部就是上面显示的获取数据的过程，且直接得到小批量数据

初始化模型参数

num_inputs = 784    #本示例中的图像是28*28,一个像素就是一个特征，因此共有784个特征
num_outputs = 10   #共10个类别

W = nd.random.normal(scale=0.01, shape=(num_inputs, num_outputs))  #随机产生标差为0.01，均值为0的权重参数，该矩阵大小为784*10
b = nd.zeros(num_outputs)   #产生偏差矩阵，10*1大小
//附上梯度
W.attach_grad()
b.attach_grad()

实现softmax运算

定义softmax函数，参数X是一个矩阵，其行数是样本数，列是输出的个数

def softmax(X):
    X_exp = X.exp()    #对矩阵中的每个元素做指数
    partition = X_exp.sum(axis=1, keepdims=True)    #参照前面的 softmax理论运算的表达式，先对每个元素秋指数，在都同行元素求和
    return X_exp / partition  # 令矩阵每行元素与改行元素的和相除。

下面用一个示例看softmax（）的运算

X = nd.random.normal(shape=(2, 5))
print("X:",X)
X_prob = softmax(X)
X_prob, X_prob.sum(axis=1)

输出如下：
X: 这是随机生成的符合正态分布的矩阵X，2行5列
[[ 1.6839303 1.2573646 0.13123232 1.6403018 -1.2138013 ]
[ 2.3999705 -0.38509098 -0.98780406 0.95858884 -1.4976466 ]]
<NDArray 2x5 @cpu(0)>
下面是经过softmax运算后，对每一个元素求指数，将其变为正数，且小于1
(
[[0.34759867 0.22689399 0.07357834 0.33275956 0.01916943]
[0.73942626 0.0456413 0.02498061 0.1749487 0.01500311]]
<NDArray 2x5 @cpu(0)>,
对每一行求和，会发现和为1
[1. 1.]
<NDArray 2 @cpu(0)>)

定义模型及损失函数

定义模型：此处定义net，参数为输入的特征矩阵，返回的是经过softmax运算后的每个类别的概率输出预测。

def net(X):
   return softmax(nd.dot(X.reshape((-1, num_inputs)), W) + b)  --reshape函数将图像改为长度为784的向量

定义损失函数：

def cross_entropy(y_hat, y):
    return -nd.pick(y_hat, y).log()
 //定义准确率
 def accuracy(y_hat, y):
    return (y_hat.argmax(axis=1) == y.astype('float32')).mean().asscalar()

这样就可以确定定义的模型在数据集上的准确率。

多层感知机MLP中的激活函数

ReLU函数

$$\text{ReLU}(x)=\max (x,0).$$

// 定义绘图函数xyplot
%matplotlib inline
import d2lzh as d2l
from mxnet import autograd, nd

def xyplot(x_vals, y_vals, name):
    d2l.set_figsize(figsize=(5, 2.5))
    d2l.plt.plot(x_vals.asnumpy(), y_vals.asnumpy())
    d2l.plt.xlabel('x')
    d2l.plt.ylabel(name + '(x)')
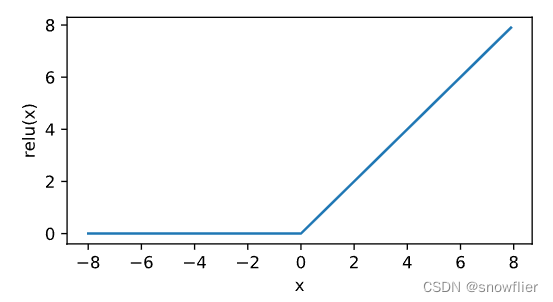
//画ReLu
x = nd.arange(-8.0, 8.0, 0.1)   --得到一个从-8到8，步长0.1的向量
x.attach_grad()
with autograd.record():
    y = x.relu()
xyplot(x, y, 'relu')
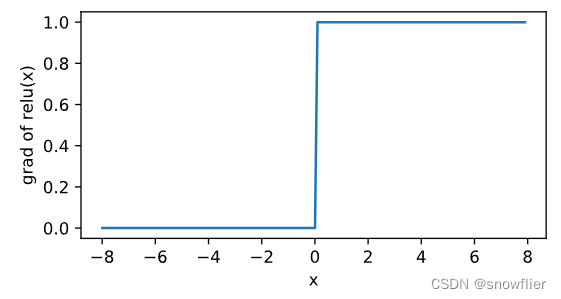
//负数时，ReLU函数的导数为0；当输入为正数时，ReLU函数的导数为1
y.backward()
xyplot(x, x.grad, 'grad of relu')

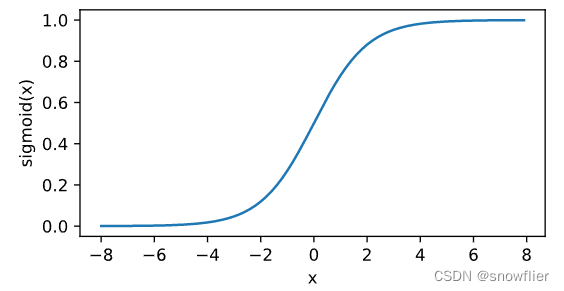
sigmoid函数

对同一个矩阵观察其sigmoid函数，将元素的值变换到0和1之间：
$$\text{sigmoid}(x)=\frac{1}{1+\exp (-x)}.$$
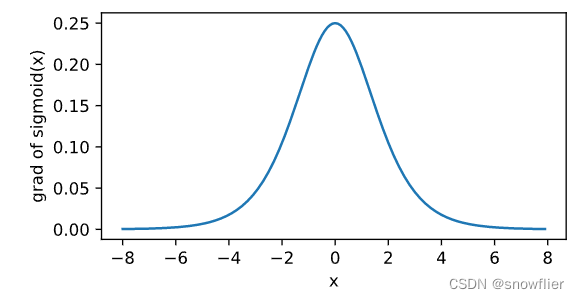
对该函数求导，显然
$${\text{sigmoid}}^{\prime }(x)=\text{sigmoid}(x)\left(1-\text{sigmoid}(x)\right).$$

with autograd.record():
    y = x.sigmoid()
xyplot(x, y, 'sigmoid')
y.backward()
xyplot(x, x.grad, 'grad of sigmoid')

多层感知机的实现

导入需要的包及模块

%matplotlib inline
import d2lzh as d2l
from mxnet import nd
from mxnet.gluon import loss as gloss

获取同样的数据

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

定义特征数，输出类别数及隐藏层的单元个数

num_inputs, num_outputs, num_hiddens = 784, 10, 256
//随机产生参数
W1 = nd.random.normal(scale=0.01, shape=(num_inputs, num_hiddens))   ---从输入到隐藏层的参数，784*256
b1 = nd.zeros(num_hiddens)
W2 = nd.random.normal(scale=0.01, shape=(num_hiddens, num_outputs))  --从隐藏层到输出层的参数，256*10
b2 = nd.zeros(num_outputs)
params = [W1, b1, W2, b2]

for param in params:
    param.attach_grad()

用max函数定义ReLU

def relu(X):
    return nd.maximum(X, 0)

定义模型，首先用reshape将原始图像变为长度为784的向量，在利用dot做线性加权求和运算，即得到隐藏层的输出，对该数值进行非线性的relu变换，将数值限定为正，再将隐藏层的输出进行线性加权得到输出

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(nd.dot(X, W1) + b1)
    return nd.dot(H, W2) + b2

定义损失函数

loss = gloss.SoftmaxCrossEntropyLoss()

定义训练模型，迭代次数为5，学习率为0.5

num_epochs, lr = 5, 0.5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params, lr)