算法导论-----最长公共子序列LCS（动态规划）

目录

• 一.概念梳理
• 二.最长公共子序列解决方案
  
  • 方案1：蛮力搜索策略
  • 方案2：动态规划策略
• 三、C代码实现
  
  • 实现1
  • 实现2(空间优化)

---

一.概念梳理

  1. 子序列(subsequence)： 一个特定序列的子序列就是将给定序列中零个或多个元素去掉后得到的结果(不改变元素间相对次序)。例如序列 <A,B,C,B,D,A,B> <script type="math/tex" id="MathJax-Element-170"> </script>的子序列有： <A,B> <script type="math/tex" id="MathJax-Element-171"> </script>、 <B,C,A> <script type="math/tex" id="MathJax-Element-172"> </script>、 <A,B,C,D,A> <script type="math/tex" id="MathJax-Element-173"> </script>等。
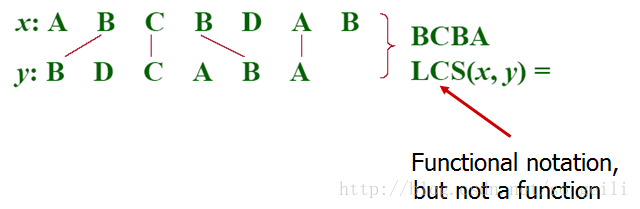
   2.公共子序列(common subsequence)： 给定序列X和Y，序列Z是X的子序列，也是Y的子序列，则Z是X和Y的公共子序列。例如 $X=<A,B,C,B,D,A,B>$， $Y=<B,D,C,A,B,A>$，那么序列 $Z=<B,C,A>$为X和Y的公共子序列，其长度为3。但 $Z$不是$X$和 $Y$的最长公共子序列，而序列$<B,C,B,A>$和 <B,D,A,B> <script type="math/tex" id="MathJax-Element-181"> </script>也均为 $X$和$Y$的最长公共子序列，长度为4，而 $X$和$Y$不存在长度大于等于5的公共子序列。
   3.最长公共子序列问题(LCS:longest-common-subsequence problem)：In the longest-common-subsequence problem, we are given two sequences $X=<x_1, x_2,... , x_m>$ and $Y=<y_1, y_2,..., y_n>$ and wish to find a (not “the”) maximum-length common subsequence of $X$ and $Y$ . This section shows how to efficiently solve the LCS problem using dynamic programming.

---

二.最长公共子序列解决方案

方案1：蛮力搜索策略

蛮力搜索策略的步骤如下：

1. 枚举序列$X$里的每一个子序列$x_i$；
2. 检查子序列$x_i$是否也是$Y$序列里的子序列；
3. 在每一步记录当前找到的子序列里面的最长的子序列。

蛮力策略也叫做暴力穷举法，是所有算法中最直观的方法，但效率往往也是最差的。在第1步枚举$X$中所有的子序列有$2^m$个，每个子序列在$Y$中检查时间复杂度为$O(n)$。因此蛮力策略的最坏时间复杂度为$O(n2^m)$，这是指数级算法，对较长的序列求LCS是不适用的。

---

方案2：动态规划策略

• LCS问题具有最优子结构
  令 $X=<x_1, x_2,... , x_m>$ 和 $Y=<y_1, y_2,..., y_n>$ 为两个序列，$Z=<z_1,z_2,z_3,...,z_k>$为$X$和$Y$的任意LCS。则

如果$x_m=y_n$，则$z_k=x_m=y_n$且$Z_{k-1}$是$X_{m-1}$和$Y_{n-1}$的一个LCS。
如果$x_m≠y_n$，那么$z_k≠x_m$，意味着$Z$是$X_{m-1}$和$Y$的一个LCS。
如果$x_m≠y_n$，那么$z_k≠y_n$，意味着$Z$是$X$和$Y_{n-1}$的一个LCS。

  从上述的结论可以看出，两个序列的LCS问题包含两个序列的前缀的LCS，因此，LCS问题具有最优子结构性质。在设计递归算法时，不难看出递归算法具有子问题重叠的性质。
  设$C[i,j]$表示$X_i$和$Y_j$的最长公共子序列LCS的长度。如果$i=0$或$j=0$,即一个序列长度为$0$时，那么LCS的长度为0。根据LCS问题的最优子结构性质，可得如下公式：

$$C[i,j]= \begin{cases} 0， & 当 i=0或j=0\\ C[i-1,j-1]+1，&当i,j>0 且x_i=y_j \\ MAX(C[i,j-1],C[i-1,j])&当i,j>0且x_i≠y_j \end{cases}$$
根据上述的递归公式和初值，有如下伪代码和实现。

• 伪代码1（递归）：计算LCS的长度

• 伪代码2（非递归）：计算LCS的长度

• 伪代码：构造一个LCS

三、C代码实现

C代码实现1

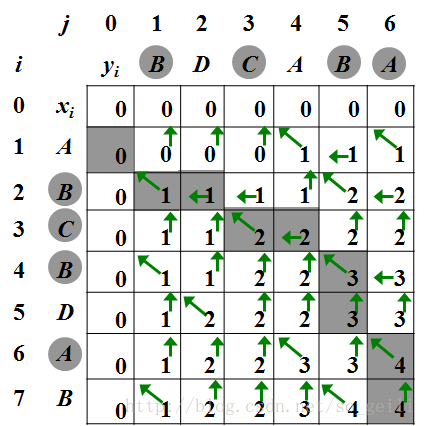
  实现1是完全按照《算法导论》中的伪代码编写而成。整个过程中表c和b的内容如下图所示：

#include <stdio.h>
#include <string.h>
#define MAXLEN 50

void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN], int b[][MAXLEN])
{
    int i, j;

    for(i = 0; i <= m; i++)
        c[i][0] = 0;
    for(j = 1; j <= n; j++)
        c[0][j] = 0;
    for(i = 1; i<= m; i++)
    {
        for(j = 1; j <= n; j++)
        {
            if(x[i-1] == y[j-1])
            {
                c[i][j] = c[i-1][j-1] + 1;
                b[i][j] = 1;                    //如果使用'↖'、'↑'、'←'字符，会有警告，也能正确执行。
            }                                   //本算法采用1,3,2三个整形作为标记
            else if(c[i-1][j] >= c[i][j-1])
            {
                c[i][j] = c[i-1][j];
                b[i][j] = 3;
            }
            else
            {
                c[i][j] = c[i][j-1];
                b[i][j] = 2;
            }
        }
    }
}

void PrintLCS(int b[][MAXLEN], char *x, int i, int j)
{
    if(i == 0 || j == 0)
        return;
    if(b[i][j] == 1)
    {
        PrintLCS(b, x, i-1, j-1);
        printf("%c ", x[i-1]);
    }
    else if(b[i][j] == 3)
        PrintLCS(b, x, i-1, j);
    else
        PrintLCS(b, x, i, j-1);
}

int main()
{
    char x[MAXLEN] = {"ABCBDAB"};
    char y[MAXLEN] = {"BDCABA"};

    int  b[MAXLEN][MAXLEN];                        //传递二维数组必须知道列数，所以使用MAXLEN这个确定的数
    int  c[MAXLEN][MAXLEN];

    int m, n;

    m = strlen(x);
    n = strlen(y);

    LCSLength(x, y, m, n, c, b);
    PrintLCS(b, x, m, n);

    return 0;
}

  最终屏幕输出的结果为：B C B A 。完全正确。

实现2(空间优化)

  实现1中用了两个二维的表b和c，在时空开销上有改进的余地。我们完全可以去掉表b。因为每个$c[i][j]$只依赖于$c[i-1][j]$、$c[i][j-1]$、$c[i-1][j-1]$三项，当给定$c[i][j]$时，我们可以在$O(1)$的时间内判定出$c[i][j]$是使用了三项中的哪一项。从而节约了$Θ(mn)$的空间。

#include <stdio.h>
#include <string.h>
#define MAXLEN 50

void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN]) {
    int i, j;

    for(i = 0; i <= m; i++)
        c[i][0] = 0;
    for(j = 1; j <= n; j++)
        c[0][j] = 0;
    for(i = 1; i<= m; i++) {
        for(j = 1; j <= n; j++) {
            if(x[i-1] == y[j-1]) {                          //仅仅去掉了对b数组的使用，其它都没变
                c[i][j] = c[i-1][j-1] + 1;
            } else if(c[i-1][j] >= c[i][j-1]) {
                c[i][j] = c[i-1][j];
            } else {
                c[i][j] = c[i][j-1];

            }
        }
    }
}
/*
void PrintLCS(int c[][MAXLEN], char *x, int i, int j) {         //非递归版PrintLCS
    static char s[MAXLEN];
    int k=c[i][j];
    s[k]='\0';
    while(k>0){
        if(c[i][j]==c[i-1][j]) i--;
        else if(c[i][j]==c[i][j-1]) j--;
        else{
            s[--k]=x[i-1];
            i--;j--;
        }
    }
    printf("%s",s);
}
*/
void PrintLCS(int c[][MAXLEN], char *x, int i, int j) {
    if(i == 0 || j == 0)
        return;
    if(c[i][j] == c[i-1][j]) {
        PrintLCS(c, x, i-1, j);
    } else if(c[i][j] == c[i][j-1])
        PrintLCS(c, x, i, j-1);
    else {
        PrintLCS(c, x, i-1, j-1);
        printf("%c ",x[i-1]);
    }
}

int main() {
    char x[MAXLEN] = {"ABCBDAB"};
    char y[MAXLEN] = {"BDCABA"};
    //char x[MAXLEN] = {"ACCGGTCGAGTGCGCGGAAGCCGGCCGAA"}; //算法导论上222页的DNA的碱基序列匹配
    //char y[MAXLEN] = {"GTCGTTCGGAATGCCGTTGCTCTGTAAA"};

    int  c[MAXLEN][MAXLEN];     //仅仅使用一个c表

    int m, n;

    m = strlen(x);
    n = strlen(y);

    LCSLength(x, y, m, n, c);
    PrintLCS(c, x, m, n);

    return 0;
}

  第一组测试序列，最终屏幕输出的结果为：B C B A 。完全正确。
  第二组测试序列，最终屏幕输出的结果为：G T C G T C G G A A G C C G G 。和教材提供的结果相同，完全正确。