感知机：函数与逻辑运算

函数包含自变量，因变量与映射。

首先定义一个函数，其数学表达式为

 通过调整常量A，B，C的取值，观察函数f(x1,x2)的输出有什么规律。

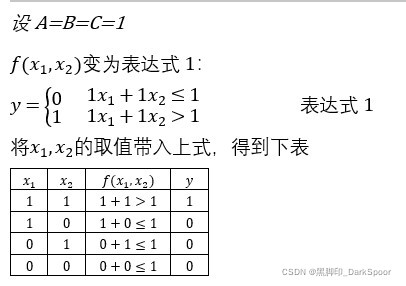
 将上表和逻辑与真值表做对比，会发现它们的运算结果是一致的。

与真值表：

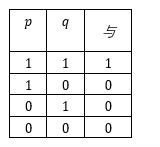
 调整常量的值，比如A=0.5   B=0.5   C=0.7 时，也可以得到逻辑与的运算结果。可见常量A,B,C的取值不是唯一的。

与非真值表

 

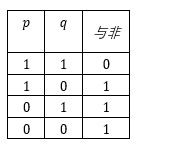
 计算结果和与非真值表是一致的。

或真值表

 

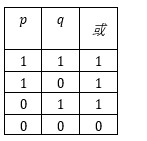
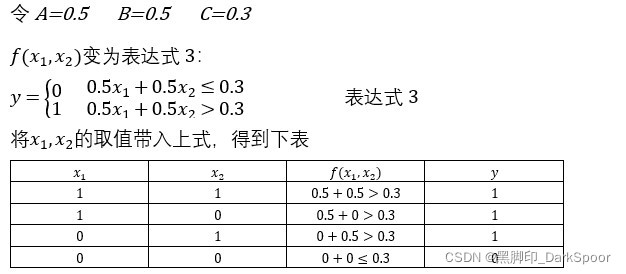
 计算结果和或真值表是一致的。

表达式1、表达式2、表达式3的定义域、值域都是一样的，类似于被线性表达，区别是只有常量A,B,C的取值不一样，选取不同的常量，实现了相应的与门、与非门、或门的运算。这里的常量是人为选择的，在解决实际问题时，常量A,B,C是通过计算(训练)得出的。

将表达式

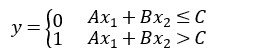
 改为图像表达，如下:

 

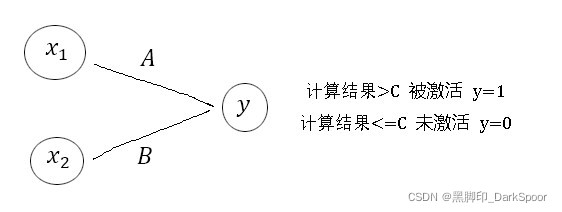
上图就是一个具有两个输入的感知机。是输入信号，是输出信号，是的权重，是阈值。

将输入增加到n个{}，常量变为权重{}，常量C换为，得到有n个输入感知机的图像表达：

 

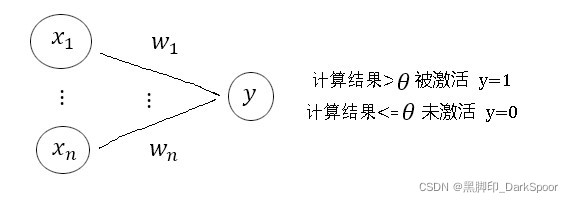
 对应的函数表达式为：

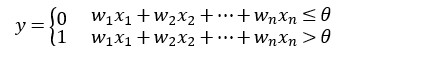
 设   ，还可以写成矩阵形式

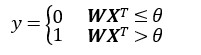
构成复杂神经网络的单细胞生物——感知机诞生了。

感知机由美国学者FrankRosenblatt在1957年提出。