从思想方法上可将算法归为以下几种:直接法、枚举法、递推法、递归法、回溯法等等。本节先介绍直接法、枚举法、递推法的思想,其他算法将在后续内容中逐步介绍。
直接法 :根据问题给出的条件直接求解。
【例2.19】 用筛选法求100之内的所有素数,并将这些素数输出。
#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
const int n=100;
int main(){
int a[n];
int i,j;
for(i=0;i<n;i++) a[i]=1+i; //用数组保存整数1-100
a[0]=0; //1不是素数,置0
for(i=1;i<n;i++){
if(a[i]==0) continue; //该数已经置0,判断下一个数
for(j=i+1;j<n;j++) if(a[j]%a[i]==0) a[j]=0; //是a[i]倍数的元素置0;
}
int count=0;
cout<<"1-" <<n<<"之间的素数:"<<endl;
for(i=0;i<n;i++) //输出所有素数
if(a[i]!=0){ //非0元素即为素数
cout<<setw(6)<<a[i];
count++;
if(count%10==0) cout<<endl; //每行10个数据
}
cout<<endl;
return 0;
}
枚举法 :在有限范围内列举所有可能的结果,找出其中符合要求的解,又称“穷举法”。其适合求解的问题是:可能的答案是有限个且答案是可知的,但又难以用解析法描述。通常,用循环结构来完成。
【例2.20】 中国古代数学史上著名的“百鸡买百鸡问题”:鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一。百钱买百鸡,问鸡翁、母、雏各几何?
#include <iostream>
#include <iomanip>
using namespace std;
int main(){
int i,j,k;
cout<<" 公鸡 母鸡 小鸡"<<endl;
for(i=0;i<=20;i++)
for(j=0;j<=33;j++){
k=100-i-j;
if((5*i+3*j+k/3==100)&&(k%3==0)) //注意(k%3==0)非常重要
cout<<setw(6)<<i<<setw(10)<<j<<setw(10)<<k<<endl;
}
return 0;
}
递推法 :通过问题的一个或多个已知解,用同样的方法逐个推算出其他解,如数列问题,近似计算问题等。通常,也要借助于循环结构完成。
【例2.21】用欧几里德算法(也称辗转法)求两个整数的最大公约数。
【分析】假定两个整数分别为num1和num2,最大公约数应当是不超过其中较小数的一个整数。辗转法的思想是:用num1除以num2,求出余数resd,如果resd==0,则当前num2就是最大公约数,否则(resd!=0),num1=num2, num2=resd, 重复以上过程,直到resd==0为止。
#include<iostream>
using namespace std;
int main(){
int num1,num2,resd;
cout<<"输入两个整数:"<<endl;
cin>>num1>>num2;
cout<<num1<<"和"<<num2<<"的最大公约数为:";
for(;;){
resd=num1%num2;
if(resd==0) break;
num1=num2; num2=resd;
}
cout<<num2<<endl;
return 0;
}
【例2.22】 输入一个小于1的数x,求sinx的近似值,要求误差小于0.0001。sinx的近似计算公式如下:
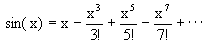
#include<iostream>
using namespace std;
int main(){
const double epsilon=0.0001; //用epsilon保存误差
double x,sinx,item;
int n=2,sign=-1; //sign保存符号
cout<<"input x:";
cin>>x;
sinx=x;item=x*x*x/6; //第一项作为初值,第二项为误差项
while(item>epsilon){
sinx=sinx+item*sign; //将当前项累加进结果,注意符号作为因子
item=item*x*x/((2*n)*(2*n+1)); //推算新的误差项
sign=-sign; //注意符号的变换
n++;
}
cout<<"sin("<<x<<")="<<sinx<<endl;
return 0;
}
【例2.23】输入一个8位二进制数,将其转换为十进制数输出。
#include<iostream>
using namespace std;
const int n=8;
int main(){
char bin[n];
int x=2,a,dec,i;
cout<<"输入二进制序列:"<<endl;
for(i=n-1;i>=0;i--) cin>>bin[i]; //先输入的是高位数
dec=0;
for(i=n-1;i>=0;i--){
a=bin[i]-'0'; //数字字符转换为数字
dec= dec*x+a;
}
cout<<"二进制序列(";
for(i=n-1;i>=0;i--) cout<<bin[i];
cout<<")的值为:"<<dec<<endl;
return 0;
}
直接法 :根据问题给出的条件直接求解。
【例2.19】 用筛选法求100之内的所有素数,并将这些素数输出。
#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
const int n=100;
int main(){
int a[n];
int i,j;
for(i=0;i<n;i++) a[i]=1+i; //用数组保存整数1-100
a[0]=0; //1不是素数,置0
for(i=1;i<n;i++){
if(a[i]==0) continue; //该数已经置0,判断下一个数
for(j=i+1;j<n;j++) if(a[j]%a[i]==0) a[j]=0; //是a[i]倍数的元素置0;
}
int count=0;
cout<<"1-" <<n<<"之间的素数:"<<endl;
for(i=0;i<n;i++) //输出所有素数
if(a[i]!=0){ //非0元素即为素数
cout<<setw(6)<<a[i];
count++;
if(count%10==0) cout<<endl; //每行10个数据
}
cout<<endl;
return 0;
}
枚举法 :在有限范围内列举所有可能的结果,找出其中符合要求的解,又称“穷举法”。其适合求解的问题是:可能的答案是有限个且答案是可知的,但又难以用解析法描述。通常,用循环结构来完成。
【例2.20】 中国古代数学史上著名的“百鸡买百鸡问题”:鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一。百钱买百鸡,问鸡翁、母、雏各几何?
#include <iostream>
#include <iomanip>
using namespace std;
int main(){
int i,j,k;
cout<<" 公鸡 母鸡 小鸡"<<endl;
for(i=0;i<=20;i++)
for(j=0;j<=33;j++){
k=100-i-j;
if((5*i+3*j+k/3==100)&&(k%3==0)) //注意(k%3==0)非常重要
cout<<setw(6)<<i<<setw(10)<<j<<setw(10)<<k<<endl;
}
return 0;
}
递推法 :通过问题的一个或多个已知解,用同样的方法逐个推算出其他解,如数列问题,近似计算问题等。通常,也要借助于循环结构完成。
【例2.21】用欧几里德算法(也称辗转法)求两个整数的最大公约数。
【分析】假定两个整数分别为num1和num2,最大公约数应当是不超过其中较小数的一个整数。辗转法的思想是:用num1除以num2,求出余数resd,如果resd==0,则当前num2就是最大公约数,否则(resd!=0),num1=num2, num2=resd, 重复以上过程,直到resd==0为止。
#include<iostream>
using namespace std;
int main(){
int num1,num2,resd;
cout<<"输入两个整数:"<<endl;
cin>>num1>>num2;
cout<<num1<<"和"<<num2<<"的最大公约数为:";
for(;;){
resd=num1%num2;
if(resd==0) break;
num1=num2; num2=resd;
}
cout<<num2<<endl;
return 0;
}
【例2.22】 输入一个小于1的数x,求sinx的近似值,要求误差小于0.0001。sinx的近似计算公式如下:
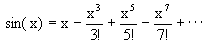
#include<iostream>
using namespace std;
int main(){
const double epsilon=0.0001; //用epsilon保存误差
double x,sinx,item;
int n=2,sign=-1; //sign保存符号
cout<<"input x:";
cin>>x;
sinx=x;item=x*x*x/6; //第一项作为初值,第二项为误差项
while(item>epsilon){
sinx=sinx+item*sign; //将当前项累加进结果,注意符号作为因子
item=item*x*x/((2*n)*(2*n+1)); //推算新的误差项
sign=-sign; //注意符号的变换
n++;
}
cout<<"sin("<<x<<")="<<sinx<<endl;
return 0;
}
【例2.23】输入一个8位二进制数,将其转换为十进制数输出。
#include<iostream>
using namespace std;
const int n=8;
int main(){
char bin[n];
int x=2,a,dec,i;
cout<<"输入二进制序列:"<<endl;
for(i=n-1;i>=0;i--) cin>>bin[i]; //先输入的是高位数
dec=0;
for(i=n-1;i>=0;i--){
a=bin[i]-'0'; //数字字符转换为数字
dec= dec*x+a;
}
cout<<"二进制序列(";
for(i=n-1;i>=0;i--) cout<<bin[i];
cout<<")的值为:"<<dec<<endl;
return 0;
}






















 1337
1337

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








