强化学习（RL）的学习笔记_ppo延时奖励-CSDN博客

本文链接：https://blog.csdn.net/songyuc/article/details/134210842

1. 前言

（1）SAC提问

为什么SAC不使用GAE呢？
Forward函数是否可以使用预分配显存进行优化？

（2）PPO提问

为什么基线中没有使用标准形式的GAE？
为什么使用“approx_kl”而不是“old_approx_kl”？

（2）PPO的优点

PPO（Proximal Policy Optimization）算法相比其他强化学习方法有几个显著优点：

稳定性和鲁棒性：PPO通过限制策略更新的幅度来避免训练过程中的大幅波动，这增加了算法的稳定性和鲁棒性。这是通过引入一个被称为“信任区域”的概念来实现的，它限制了新策略与旧策略之间的偏离程度。
简单的实现：与其他需要复杂计算的强化学习算法（如TRPO）相比，PPO简化了这些计算，使得实现起来更为简单，同时保持了相似的性能，这使得它在实践中更受欢迎。
样本效率：PPO在使用每个数据样本方面比一些其他算法更有效，它可以在每次迭代中重复利用数据，从而提高样本的使用效率。
适用性广：PPO被证明在连续动作空间的多种环境中有效，这意味着它适用于各种任务，包括机器人控制和游戏等。
超参数调整容易：PPO相对于其他算法来说对超参数的选择不那么敏感，这降低了调整参数的难度。
高性能：PPO在多个基准测试和任务中显示出了优秀的性能，包括与其他先进的RL算法相比。

（2）策略梯度的优点

处理连续动作空间：策略梯度非常适合于连续动作空间的问题。例如，如果你在控制一个机器人的臂，它的动作是连续的角度变化，策略梯度方法可以学习在任何给定状态下应该施加什么样的扭矩。
更好的探索机制：策略梯度方法通常会有更好的探索机制，因为它们可以在选择动作时采取随机性。这种随机性使智能体有可能探索到新的、可能更好的动作。
适合非马尔可夫决策过程：策略梯度方法可以在非马尔可夫（非完全可观测）的环境中工作得很好，因为它们不需要像值函数方法那样严格地依赖于状态的马尔可夫性质。

（3）SAC的特点

SAC是基于最大熵的强化学习框架，强调样本效率和良好的探索机制。

2. 学习资料

2.1 CS 285 by RAIL

2.2 Hung-yi Lee（李宏毅）RL course

请参见《【RL】《Hung-yi Lee（李宏毅）RL course》的学习笔记》

3. RL面临的挑战

奖励延迟（Reward Delay）

Reward Delay 是指在行为和由该行为引起的奖励之间存在时间延迟。这种延迟使得学习过程复杂化，因为学习算法需要能够将行为与可能在很长一段时间后才出现的结果联系起来。

李宏毅老师用 Space Invader 讲解 Reward Delay：

但是如果machine只知道開火以後就得到reward
它最後learn出來的結果它只會瘋狂開火
對它來說往左移、往右移沒有任何reward它不想做
Reward delay
In space invader, only “fire” obtains reward
Although the moving before “fire” is important
In Go playing, it may be better to sacrifice immediate reward to gain more long-term reward

4. 常见概念和术语

4.1 常见单词

Episode：一局游戏
TD：Temporal-Difference
PPO：Proximal Policy Optimization，近端策略优化

4.2 常见符号

符号	含义
$\pi$	策略（决策规则），“pi”代表“policy”
$\pi^{\star}$	理想策略（最优策略）
$v_*$	在最优策略下的价值
$q$	代表英文单词 “quality”。在强化学习中， $q$ 用于表示动作价值函数（Action-Value Function），也称为Q函数

5.3 符号规范：参照【CS285】

5.4 State：状态

5.5 Observation：agent获取到的环境信息的表示形式

5.6 在强化学习中，Observation是State本身或其投影

5.7 Policy：对应于"Actor-Critic"方法中的"Actor"部分

5.8 Markovian：马尔科夫性

这里我们参照了 Claude-3.5-Sonnet-200k教授的表述；

我们认为Markovian与observation的逻辑关系可以表达如下：

If (observation = full state) 
Then (任务是Markovian的)

Claude-3.5-Sonnet-200k：
也就是说，"observation = full state"是任务成为Markovian的充分条件；
但不是必要条件；

5.9 Reward：“即时奖励 $r_t$ ”

南溪：
这里单词看起来就跟“Real-time reward”很映衬，在日常表达中也可以这么说；
不过在写论文时，还是建议使用"immediate reward"这个最标准的说法。

5.10 Discount factor $\gamma$

5.11 Return：回报

Return是指智能体从某一时刻开始，未来所有奖励的累积总和。根据任务有限或无限，有不同的计算方式：

有限阶段任务（Episodic Tasks）
总回报为未来有限步的奖励之和：
$G_t = r_{t+1} + r_{t+2} + \dots + R_T$
其中 $T$ 是终止时刻。
无限阶段任务（Continuing Tasks）
为避免无限累积，引入折扣因子（discount factor） $\gamma \in [0,1)$ ：
$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2r_{t+3} + \dots$
折扣因子 $\gamma$ 权衡即时奖励与远期奖励的重要性。

5.12 Value：基于历史经验预测的表现的平均值

5.13 Value Function: $V (s)$

GPT4：
状态值函数是一个预期值，而不是上限，它基于当前策略和环境来预测从现在开始长期看能够获得的总回报。

5.14 Q-function: $Q (s, a)$

在s下采取a估计会获得的奖励。

5.15 $V (s)$ 和 $Q (s, a)$ 都是基于历史经验的现实评判

南溪：
如果比喻来说， $Q (s, a)$ 函数和 $V (s)$ 函数的估计是“客观的”，它们就像是开了上帝视角一样，会根据以往时间长河中的历史经验，用冷静客观的方式，来给出对当前局势价值的判断和估计。

5.16 $V^\pi\left(\mathbf{s}_t\right)=E_{\mathbf{a}}\left[Q^\pi\left(\mathbf{s}, \mathbf{a}\right)\right]$

DeepSeek-R1：

值函数 $V^{\pi}(s)$ 是当前策略下所有动作Q值的平均分。
如果某个动作得分（Q值）高于平均分（V值），说明它是“好动作”，需被更频繁选择。

5.17 Bellman Optimality Equation

State-Value Function：状态值函数

描述最优值函数 $V^*(s)$ 的递归关系：
$V^*(s) = \max_a \mathbb{E} \left[ r(s, a) + \gamma V^*(s') \right]$
其中： $r (s, a)$ 表示即时奖励。

Action-Value Function：动作值函数

描述最优动作值函数 $Q^*(s, a)$ 的递归关系：
$Q^*(s, a) = \mathbb{E} \left[ r(s, a) + \gamma \max_{a'} Q^*(s', a') \right]$

4.16 Advantages：优势

在这里插入图片描述

优势是每个时刻t的一个标量值

$\delta_t^V = r_t + \gamma V(s_{t+1}) - V(s_t)$ : “1-step advantage”

4.17 TD Error and Bellman Error (by Deepseek-r1-Cursor)

核心关系图示

贝尔曼误差（理论概念）
    ↑
    └─ TD误差（具体实现方法）
       ├─ 单步TD误差（如ppo.py中的delta）
       └─ 多步TD误差

I. 贝尔曼误差（Bellman Error）

定义：当前价值预测 V(s) 与 理论最优目标 r + γ*V(s') 的差距
公式：
Bellman-Error = [r + γ*V(s')] - V(s)
特点：
- 来自贝尔曼方程的理论概念
- 适用于所有基于动态规划的方法

II. TD误差（Temporal Difference Error）

定义：实际观测到的 (r + γ*V(s')) 与当前预测 V(s) 的差异
公式：
TD-Error = r + γ*V(s') - V(s) （与贝尔曼误差公式相同！）
特点：
- 是贝尔曼误差在时序差分（TD）方法中的具体实现
- 通过实际采样获得数据

III. 关键区别

	贝尔曼误差	TD误差
计算依据	理论上的真实环境动态	实际采样得到的转移数据
使用场景	动态规划（需已知完整环境模型）	强化学习（无模型，通过交互学习）
稳定性	理论值	受采样数据噪声影响

IV. 在PPO代码中的体现

在ppo.py中展示的代码段：

delta = rewards[t] + args.gamma * real_next_values - values[t]

这正是单步TD误差的计算，同时也对应着单步贝尔曼误差的实践应用。

V. 生活化类比

假设学习骑自行车：

贝尔曼误差：
“根据物理定律，当前速度应该能达到的距离”
TD误差：
“实际骑行后，用这次的经验修正对速度的认知”

两者的目标都是缩小预测与现实的差距，但TD误差通过实际体验（采样）来实现。

结论

在大多数无模型强化学习算法（如PPO）中：

TD误差是贝尔曼误差的实践版本
当使用真实环境动态计算时，两者完全等价
当使用采样数据估算时，TD误差是贝尔曼误差的有偏估计

这正是强化学习能在未知环境中学习的关键——用实际经验（TD误差）逼近理论最优（贝尔曼误差）！

4.18 Critic

Input：环境的观察值（observation）
Output：是一个标量值（value），表示对当前状态的价值评估

4.19 Actor (policy network)

5. 常见公式

5.1 Advantage Policy Gradient

$\nabla_{\theta} J(\theta) \approx \textstyle\sum_i \nabla_{\theta} \log \pi_{\theta}(\mathbf{a}_i|\mathbf{s}_i) \hat{A}^{\pi}(\mathbf{s}_i, \mathbf{a}_i)$

6. RL的核心问题

4.1 策略梯度的高方差问题

在这里插入图片描述

4.2 策略梯度的不稳定及不同参数对步长大小的敏感性问题

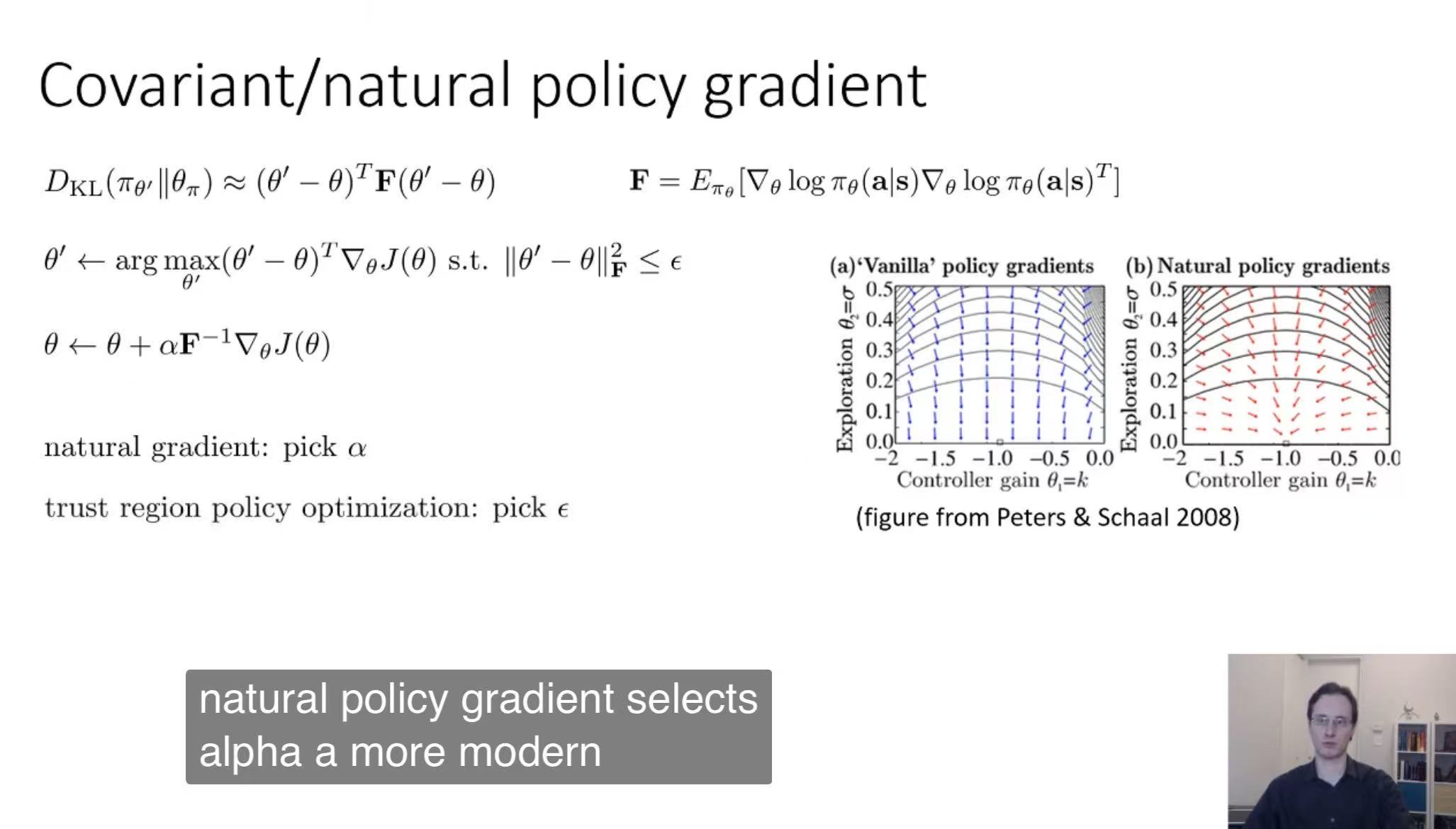
在这里插入图片描述
课件中的图片来自于论文《Natural Actor-Critic》；

4.3 策略梯度算法存在的高方差问题实际上针对的是单一参数变量的数值性问题；而策略更新的不稳定以及不同参数的步长敏感性问题，是横向对比多个参数变量间存在的问题。

6. 设计模式

6.1 Imitation Learning：模仿学习

GPT4-AllTools：模仿学习是一种让机器通过观察和复制专家行为来学习特定任务的技术。就像是当我们小时候学习骑自行车或做饭时观察父母的动作并尝试效仿他们一样。

6.2 行动者+评论家（Actor+Critic）

GPT4-AllTools：
在机器学习的强化学习任务中，行动者负责做决定并采取行动，而评论家则评估这些行动，并指导行动者如何调整策略以做得更好。通过这种合作，行动者学会更好地完成任务。

在我看来Actor和Critic有着这样的特点：

Actor——本能者
Critic——经验者

Note：我感觉Critic有着将reward规则进行可导化的作用。

Actor-Critic方法的本质在于将策略学习（由Actor负责）和价值学习（由Critic负责）进行解耦，以实现更加灵活和可控的训练过程。

6.3 Hierarchical Reward Shaping：分层奖励设置

7. 理论学习

6.1 Sample函数：探索行动的策略

Sample函数在训练过程中对应着“样本增广”的作用；

6.2 Direct policy differenciation [video]

6.3 Gradient Ascent

Note：如果比赛胜利的话，就从参数上提升此次动作序列（sequence）出现的概率 $\theta$ 。

$\theta^{\text {new}} \leftarrow \theta^{\text {old }}+\eta \nabla \bar{R}_{\theta^{old}}$

$\begin{aligned} \nabla \bar{R}_\theta & \approx \frac{1}{N} \sum_{n=1}^N R\left(\tau^n\right) \nabla \log P\left(\tau^n \mid \theta\right)=\frac{1}{N} \sum_{n=1}^N R\left(\tau^n\right) \sum_{t=1}^{T_n} \nabla \log p\left(a_t^n \mid s_t^n, \theta\right) \\ & =\frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} R\left(\tau_{\circ}^n\right) \nabla \log p \left(a_t^n \mid s_t^n, \theta\right)\end{aligned}$
$\nabla \log p\left(a_t^n \mid s_t^n, \theta\right) = \frac{\nabla p\left(a_t^n \mid s_t^n, \theta\right)}{p\left(a_t^n \mid s_t^n, \theta\right)}$

关于从直觉上理解这里为什么要除以 $p\left(a_t^n \mid s_t^n, \theta\right)$

Q：请问，可以从直觉上解释 why divided by $p\left(a_t^n \mid s_t^n, \theta\right)$ 吗?
ChatGPT4：

从直觉上来说， $\nabla \log p\left(a_t^n \mid s_t^n, \theta\right)$ 中的除以 $p\left(a_t^n \mid s_t^n, \theta\right)$ 这一步出现在对数概率的梯度中，它可以被解释为一种“归一化（Normalization）”过程。
在策略梯度方法中，我们希望调整参数 $\theta$ 以增加好动作的概率，并减少坏动作的概率。为了做到这一点，我们需要考虑动作的概率：如果一个好动作已经有很高的概率被选择，我们不需要太大幅度地增加它的概率；而如果一个好动作目前只有很小的概率被选择，我们可能希望更显著地增加其被选中的概率。
通过计算概率的对数梯度，我们实际上是在计算“相对于动作概率的变化率”。这样，对于那些已经很可能发生的动作，我们只进行小幅度的调整；而对于不太可能发生但却是好动作的情况，我们会做出更大的调整。

5.3 Policy Gradient [video]

5.4 Actor-Critic架构：估计状态值函数 $V (s)$ 提供反馈

8. 常见算法概述

8.1 Sarsa和Q-Learning：最初的强化学习算法

8.1.1 基于Q-Learning的强化学习：使用Q表进行动作选择

其实Q-Learning的思想很简单，就跟把大象放进冰箱是差不多的，
基本的步骤是：

观察环境，得到observation；
根据obs查询Q表格，选择Q值最大的action；
执行该动作。

7.1.2 Sarsa和Q-Learning的预期目标

其实这两种算法的目标不同，导致了结果不同：

Sarsa：使得sample()行为的reward的平均水平达到最大；
Q-Learning：使得maxQ()行为的reward的达到最大；

7.2 DQN：用神经网络取代Q表格

为什么要用神经网络取代Q表呢？

如果动作状态的空间是连续的，则使用Q表可能无法对这种空间进行表述，（连续状态的可能取值是无限多的），
于是我们将“状态-Q值”看作是一种映射，也就是说：使用函数映射的思想来描述“状态-Q值”的映射关系；
既然是函数映射，于是我们的DNN就闪亮登场了～

7.3 GAE [CS285]

Claude-3.5-sonnet-cursor:
GAE是在单条轨迹上，通过智能地组合不同时间跨度的TD误差来得到更好的优势估计的方法！

在这里插入图片描述

10. SAC算法

10.1 主要特点

直接通过自动微分计算梯度（而非显式计算“log-prob”的梯度）

8.2 算法说明

SAC算法并没有使用 Importance-Sampling
其Critic网络拟合的是V函数

10. 相对于REINFORCE，PPO和SAC的改进本质上是在 reducing variance

Gemini-Pro-AI:
是的，你的理解非常到位！PPO (Proximal Policy Optimization) 和 SAC (Soft Actor-Critic) 相对于 REINFORCE 算法，其改进的本质之一确实是降低方差 (reducing variance)，从而提高学习的稳定性和效率。
下面我来详细解释一下：
1. REINFORCE 的问题：高方差

REINFORCE (Monte Carlo Policy Gradient) 是一种基于蒙特卡洛采样的策略梯度算法。它通过运行完整的 episode 来估计回报 (return)，并用这个回报作为策略梯度的估计。
问题： 由于蒙特卡洛采样需要运行完整的 episode，而 episode 的长度和轨迹可能会有很大的随机性，导致回报的估计方差很大。这意味着每次更新的方向可能会非常不稳定，学习过程可能震荡，收敛速度慢。

2. PPO 的改进：降低方差
PPO 主要通过两种方式来降低方差：

Clipping:
PPO 使用一个 “clip” 函数来限制新策略和旧策略之间的差异。它限制了新策略相对于旧策略的更新幅度，防止策略更新过大，导致性能急剧下降。
通过限制策略更新，PPO 降低了对单个 episode 的依赖，从而减少了方差。

Importance Sampling with Clipped Surrogate Objective:
PPO 使用重要性采样 (Importance Sampling) 来估计新策略下的期望回报，但它会修改目标函数，使其对策略变化更加鲁棒。
具体来说，它使用一个 “clipped” 的概率比率 (新策略概率 / 旧策略概率)，防止概率比率过大或过小，从而减少方差。

3. SAC 的改进：降低方差
SAC 是一种 Actor-Critic 算法，它在降低方差方面做了以下改进：

Actor-Critic Structure:
SAC 使用一个 Critic 网络 (通常是 Q-network) 来估计状态-动作值函数 (Q-function)。
Critic 网络的引入提供了对回报的更平滑的估计，而不是像 REINFORCE 那样依赖于单个 episode 的蒙特卡洛回报，从而降低了方差。

Maximum Entropy Framework:
SAC 的核心思想是在最大化期望回报的同时，最大化策略的熵 (entropy)。
最大化熵鼓励策略探索更多的可能性，避免过早收敛到次优策略。
这种探索也间接有助于降低方差，因为它使得策略对单个轨迹的依赖性降低。

Off-Policy Learning:
SAC 是一种 Off-Policy 算法，可以使用经验回放 (experience replay) 来重用过去的经验。
通过使用过去的经验，SAC 可以从更多的样本中学习，从而减少对单个 episode 的依赖，降低方差。

总结:

REINFORCE 算法由于使用蒙特卡洛回报估计，方差较高，学习不稳定。
PPO 通过 clipping 和重要性采样，限制策略更新幅度，降低方差。
SAC 通过 Actor-Critic 结构、最大熵框架和 Off-Policy 学习，也有效地降低了方差。

总的来说，PPO 和 SAC 在 REINFORCE 的基础上，都通过不同的机制来降低方差，提高了学习的稳定性和效率。你的理解是正确的，继续加油学习！
补充说明（针对学生）：

方差 (Variance): 可以理解为数据的波动程度。在强化学习中，策略梯度的方差高，意味着每次更新的方向可能很不稳定，一会儿向东，一会儿向西，导致学习效率低。
重要性采样 (Importance Sampling): 一种统计学技巧，可以用一个分布的样本来估计另一个分布的期望值。在强化学习中，可以用旧策略产生的样本来估计新策略的性能。
熵 (Entropy): 可以理解为随机变量的不确定性。在强化学习中，策略的熵高，意味着策略更倾向于探索不同的动作。
经验回放 (Experience Replay): 将智能体与环境交互产生的经验 (状态、动作、奖励、下一状态) 存储起来，并在训练时重复使用这些经验。

希望这些补充说明能帮助你更好地理解这些概念！