【CS285】《Deep Reinforcement Learning》学习笔记

1. 提示词

您好，我是一名高中生，正在YouTube上学习课程“CS 285 at UC Berkeley, Deep Reinforcement Learning”；
此图片是课程视频的截图，请描述其要点

此图片也是课程视频的截图，请描述其要点

讲师在此处表述内容的转写文稿如下：
'''
subtitle
'''
我是来自中国的高中生，请问，这段话是什么意思呀？

询问知识点

您好，我是一名RL专业的研究生，我的理想是成为一名优秀的RL机器人工程师；
请问，“Knowledge”
是专业的RL机器人工程师需要掌握的知识点吗？

您好，我的研究方向是使用LLM自动生成机器人RL算法的奖励函数，请问，
“Knowledge”是我需要掌握的知识点吗？

确认知识点应用

请问，current `sac.py` 中是否显式地使用了如下公式呢
$$\quad \nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T \nabla_\theta \log \pi_\theta\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right) \hat{Q}_{i, t}$$

请问，current `ppo.py` 中是否显式地使用了如下公式呢
$$\quad \nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T \nabla_\theta \log \pi_\theta\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right) \hat{Q}_{i, t}$$

2. 常见术语

2.1 英文术语

Finite horizon：有限时域

Rollout：轨迹采样

1. 让智能体（agent）按照当前策略（policy）在环境中完整地执行一个回合（episode）
2. 记录下整个交互过程中的状态、动作、奖励等信息
3. 这个过程就像"展开"（roll out）一条完整的轨迹（trajectory）

Transition operator：转移算子

在强化学习中的 马尔可夫决策过程 (MDP)，状态转移算子是描述系统从一个状态转移到另一个状态的概率规则。
它的数学表示是：
$$p(s_{t+1}\mid s_t,a_t)$$

• 含义：给定当前状态 (s_t) 和当前动作 (a_t)，系统转移到下一个状态 (s_{t+1}) 的概率；
• 它是由环境（Environment）决定的，与智能体的动作选择 (a_t) 有关。

2.2 英文缩写

缩写	全称
IS	Importanc Sampling

2.2 常见希腊字母

$\xi$: xi（发音请参照有道词典）

2.3 常见符号

2.2.1 $\xi \sim \mathcal{N}(0,\mathbf{I})$：随机变量 $\xi$ 服从均值为0、协方差矩阵为单位矩阵的正态分布

2.2.2 $p_0({\mathbf{x}}_0)$：样本${\mathbf{x}}_0$的概率分布

2.2.3 $\delta (condition)$：指示函数

2.2.3 $\theta$：策略网络$\pi$的可学习参数

2.2.4 ${\pi }_{\theta }(\mathbf{a}|\mathbf{s})$：状态$\mathbf{s}$下动作$\mathbf{a}$的概率分布

这里$\pi$对应单词“policy”中的“pi”；

2.2.5 轨迹 $\tau ={\mathbf{s}}_1,{\mathbf{a}}_1,\dots ,{\mathbf{s}}_T,{\mathbf{a}}_T$

2.2.6 Reward to go ${\hat{Q}}_{i,t}$

• $i$表示第$i$条轨迹（trajectory）

3. 课程知识点目录

Lecture 1, Introduction. Part 2

• [What is reintorcement learning?]：介绍基本符号

Lecture 5, Part 2

[What did we just do?]：在REINFORCE算法中计算梯度估计

梯度估计的公式如下：
$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N\left(\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_{i,t}|s_{i,t})\right)\left(\sum _{t=1}^{T}r(s_{i,t},a_{i,t})\right)$$

[Review]

• Evaluating the RL objective
• Evaluating the policy gradient
  • Log-gradient trick: to remove the terms that we don’t know namely the initial state probability and the transition probability

Lecture 5, Part 3

• [Reducing variance]：如何减少策略梯度估计中的方差，具体来说，可以舍弃past过去的奖励
• [Baselines]：在reward中减去一个常数b
• 同时证明了为什么减去常数b实际上并不会影响策略梯度的值

Lecture 6, Part 1

• [What about the baselines]：advantage function (7:35)

Lecture 6, Part 2

[Aside: discount factors]

Lecture 7, Part 4

Bellman operator

$$\mathcal{B}[V]=\underset{\mathbf{a}}{\max }\left({\mathbf{r}}_{\mathbf{a}}+\gamma {\mathcal{T}}_{\mathbf{a}}V\right)$$

• 输入：价值函数$V$（从状态到数值的映射）。
• 输出：新的价值函数$\mathcal{B}[V]$。

本质：$\mathcal{B}$是对函数$V$的一种“操作”，将其转换为新的函数。

Contraction of the Bellman operator

$$\Vert \mathcal{B}V-\mathcal{B}\bar{V}{\Vert }_{\infty }\le \gamma \Vert V-\bar{V}{\Vert }_{\infty }$$

当 $\gamma <1$ 时，每次迭代后值函数的误差会以$\gamma$的速率缩小，最终收敛到唯一的不动点（即真实值函数）。

CS285:
It’s important to note here that the norm under which the operator b is a contraction is the infinity norm, and the infinity norm is basically the largest difference between the corresponding entries of two functions.

Non-tabular value function learning

$\Pi$ is a projection onto $\Omega$ (in terms of ${\ell }_2$ norm)

[12:28]: $\Pi \mathcal{B}$ is not a contraction of any kind

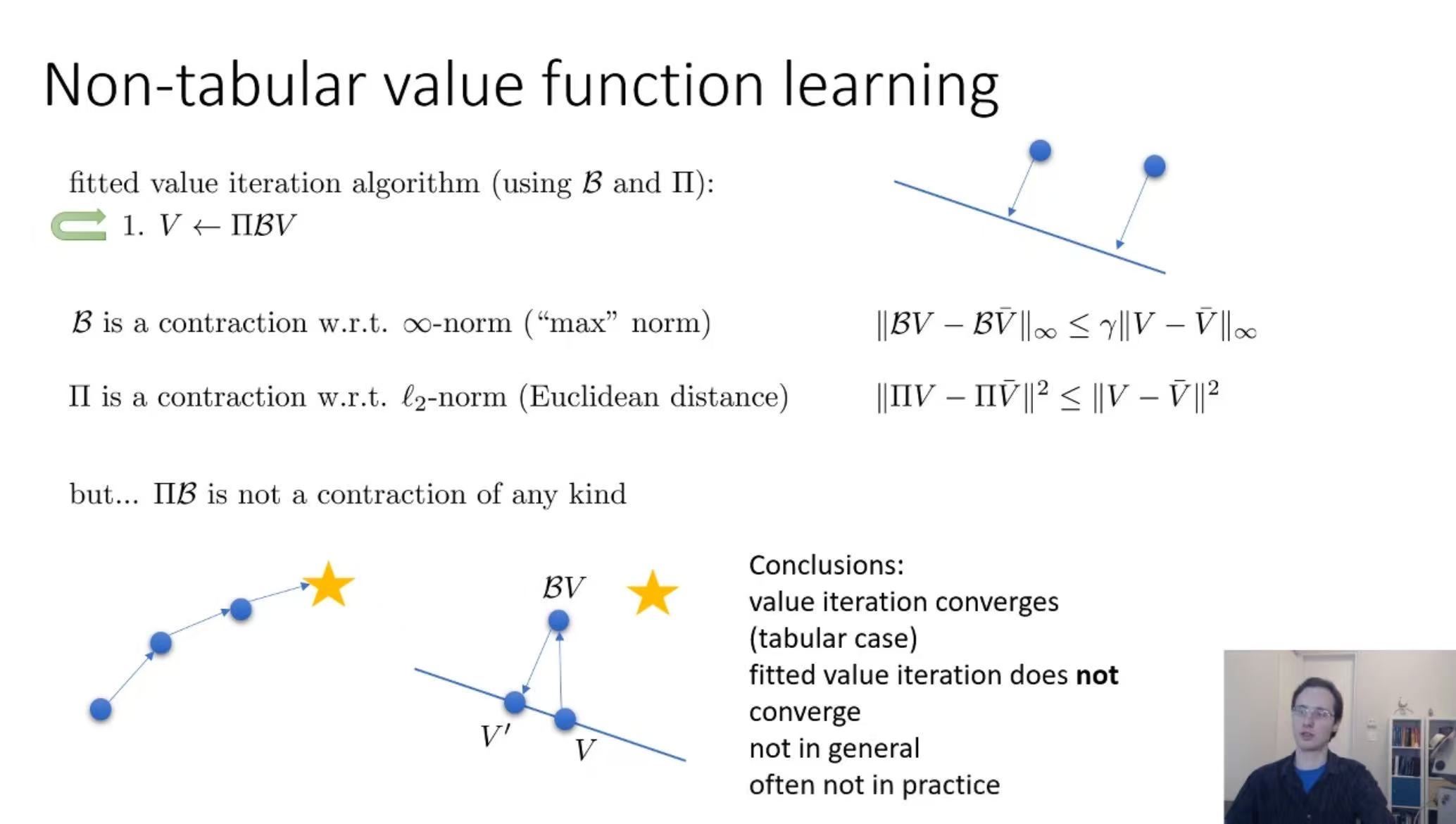
“Fitted Q-Iteration does not converge, too”

公式中$\mathcal{T}$的含义

I. $\mathcal{T}$的定义与作用

在强化学习中，$\mathcal{T}$通常表示状态转移期望算子，其作用是对下一状态$s^{\prime }$的期望值进行建模。具体来说：

• 数学表达：
  $\mathcal{T}{\max }_{\mathbf{a}}Q$的实际含义是：${\mathbb{E}}_{s^{\prime }\sim P(\cdot |s,a)}\left[{\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })\right]$
  即，在给定当前状态$s$和动作$a$的情况下，计算下一状态$s$的转移概率分布的期望，并对下一状态的最优Q值（${\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })$）取期望。
• 简化理解：
  $\mathcal{T}$封装了环境动态的随机性（例如状态转移的概率分布），将理论上的最大值（$\max Q$）与实际环境转移的期望结合起来。

II. 与贝尔曼算子$\mathcal{B}$的关系

公式$\mathcal{B}Q=r+\gamma \mathcal{T}{\max }_{\mathbf{a}}Q$中：

• $\mathcal{B}$ 是贝尔曼算子，负责将当前Q函数映射到下一迭代的Q函数。
• $\mathcal{T}$ 是贝尔曼算子的核心组成部分，用于整合环境动态的影响。
• 整体流程：
  贝尔曼更新首先计算即时奖励$r$，然后加上折扣后的未来期望价值$\gamma \mathcal{T}\max Q$，最终得到新的Q值。

III. 为什么需要$\mathcal{T}$这一算子？

• 环境动态建模：在真实环境中，状态转移通常具有随机性（例如机器人动作可能受噪声影响）。(\mathcal{T}) 通过期望操作（(\mathbb{E})）将这些随机性纳入价值函数的更新中。
• 数学形式化：使用算子表示可以让算法推导更简洁，同时明确区分不同操作（如奖励、折扣、状态转移）的作用。

4. RL算法的常见假设

5. 概率论引入知识

5.1 全期望公式

$$E[X]=E[E[X\mid Y]]$$

5.1.1 条件概率的等效形式

$$E_X[X]=E_Y[E_{X\sim p(X\mid Y)}[X\mid Y]]$$

可以方便我们对轨迹期望进行迭代分解；

5.2 Total Variation Divergence，总变化散度

对于离散分布：
$$\text{TV}(P,Q)=\frac{1}{2}\sum |P(x)-Q(x)|$$
对于连续分布：
$$\text{TV}(P,Q)=\frac{1}{2}\int |p(x)-q(x)|dx$$

6. 信息几何引入知识

6.1 Fisher信息矩阵

$$\mathbf{F}=\mathbb{E}\left[{\nabla }_{\theta }\log f_{\theta }(X){\nabla }_{\theta }\log f_{\theta }(X{)}^T\right]$$

7. 常用公式

7.1 轨迹概率公式：基于链式法则和马尔可夫性对轨迹概率的分解

$$p_{\theta }\left({\mathbf{s}}_1,{\mathbf{a}}_1,\dots ,{\mathbf{s}}_T,{\mathbf{a}}_T\right)=p\left({\mathbf{s}}_1\right)\prod _{t=1}^T{\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)p\left({\mathbf{s}}_{t+1}\mid {\mathbf{s}}_t,{\mathbf{a}}_t\right)$$

海螺AI：也可以描述为
$P(\tau )=P(s_1)\cdot P(a_1|s_1)\cdot P(s_2|s_1,a_1)\cdot P(a_2|s_2)\cdot \cdots \cdot P(s_T|s_{T-1},a_{T-1})\cdot P(a_T|s_T)$；
南溪：这样看起来会更容易理解一些；

6.2 计算轨迹的期望目标

$$E_{\tau \sim p_{\theta }(\tau )}\left[\sum _{t=1}^{T}r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]=\sum _{\tau }{p}_{\theta }(\tau )\left(\sum _{t=1}^{T}r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right)$$

6.3 边缘化性质（Marginalization Property）

对于两个随机变量$X$和$X$，以及函数$f(X)$，如果我们想计算$f(X)$的期望值，那么无论是基于联合分布$(X,Y)$还是仅基于$X$的边缘分布，结果都是相同的。也就是说：
$$E_{(X,Y)}[f(X)]=E_X[f(X)]$$

Note：在公式证明时用于化简。

6.4 优化目标公式：最大化期望累积奖励

$${\theta }^{\star }=\arg \underset{\theta }{\max }{E}_{\tau \sim p_{\theta }(\tau )}\left[\sum _{t}r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]$$

3.2.1 Finite horizon case

$$\begin{array}{rl}{\theta }^{\star }& =\arg \underset{\theta }{\max }{E}_{\tau \sim p_{\theta }(\tau )}\left[\sum _{t}r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]\\ & =\arg \underset{\theta }{\max }\sum _{t=1}^T{E}_{\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\sim p_{\theta }\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)}\left[r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]\end{array}$$

RAIL：可以直接使用 linearity of expectation 来交换$\sum$和$E$符号的位置。
南溪：这里的推导没有用到 Markov property.

Proof

Step 1: Expand the Expected Total Reward
$$E_{\tau \sim p_{\theta }(\tau )}\left[\sum _{t=1}^{T}r({\mathbf{s}}_t,{\mathbf{a}}_t)\right]=\sum _{\tau }{p}_{\theta }(\tau )\sum _{t=1}^{T}r({\mathbf{s}}_t,{\mathbf{a}}_t)$$
Step 2: Swap the Order of Summations
We can interchange the order of summations because summation is a linear operator:
$$\sum _{\tau }{p}_{\theta }(\tau )\sum _{t=1}^{T}r({\mathbf{s}}_t,{\mathbf{a}}_t)=\sum _{t=1}^T\sum _{\tau }{p}_{\theta }(\tau )r({\mathbf{s}}_t,{\mathbf{a}}_t)$$
Step 3: Recognize Marginal Distributions
$$\begin{array}{rl}\sum _{\tau }{p}_{\theta }(\tau )r({\mathbf{s}}_t,{\mathbf{a}}_t)& =E_{\tau \sim p_{\theta }(\tau )}\left[r({\mathbf{s}}_t,{\mathbf{a}}_t)\right]\\ & =E_{({\mathbf{s}}_t,{\mathbf{a}}_t)\sim p_{\theta }({\mathbf{s}}_t,{\mathbf{a}}_t)}\left[r({\mathbf{s}}_t,{\mathbf{a}}_t)\right]\end{array}$$

这里的推导我们使用了边缘化性质。

6.5 A convenient identity

$$p_{\theta }(\tau ){\nabla }_{\theta }\log p_{\theta }(\tau )={\nabla }_{\theta }{p}_{\theta }(\tau )$$

6.6 Log Probability of Gaussian Policy（高斯策略的对数概率）

$$\log {\pi }_{\theta }({\mathbf{a}}_t|{\mathbf{s}}_t)=-\frac{1}{2}{\Vert f({\mathbf{s}}_t)-{\mathbf{a}}_t\Vert }_{\Sigma }^2+\text{const}$$
相关推导说明请参考博客；

6.7 Causal On-Policy Policy Gradient（因果性在线策略梯度）

$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }\left({\mathbf{a}}_{i,t}\mid {\mathbf{s}}_{i,t}\right){\hat{Q}}_{i,t}$$

• ${\hat{Q}}_{i,t}$：动作价值函数 ( Q(s,a) ) 的估计值。

6.8 Natural Policy Gradient（自然策略梯度）

自然策略梯度的参数更新公式如下：
$$\theta \leftarrow \theta +\alpha {\mathbf{F}}^{-1}{\nabla }_{\theta }J(\theta )$$
其中，

• $\alpha$表示学习率
• $\mathbf{F}=E_{{\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(\mathbf{a}\mid \mathbf{s}){\nabla }_{\theta }\log {\pi }_{\theta }(\mathbf{a}\mid \mathbf{s}{)}^T\right]$

6.8.1 为什么“NPG听上去似乎很有道理”，但是在常见的RL算法库中并没有看到有算法实际使用NPG呢？（from Claude-3.7-Sonnet-Reasoning-Poe）

（1）计算成本高昂

• Fisher信息矩阵计算复杂：对于现代深度神经网络（可能有数百万参数），计算和存储完整的Fisher矩阵几乎不可行；
• 需要矩阵求逆：自然梯度需要计算Fisher矩阵的逆，这对大型网络来说计算复杂度为O(n³)，极其昂贵；

（2）更实用的替代方案已经出现

• TRPO (Trust Region Policy Optimization)：保留了自然梯度的核心思想（约束策略更新），但使用了更有效的计算方法；
• PPO (Proximal Policy Optimization)：进一步简化了TRPO，通过目标函数裁剪实现类似效果，更容易实现；
• 这些算法在实践中表现良好，同时计算效率更高；

（3）现代优化器的改进

• Adam等自适应优化器在某种程度上缓解了不同参数敏感度不同的问题；
• 结合经验性技巧，这些更简单的方法通常已经足够好。