专升本数学知识点看这一篇就够了！(持续更新中...)

FL不凡

已于 2025-02-06 21:55:43 修改

阅读量1.3k

点赞数 15

文章标签：笔记学习考研

于 2025-01-15 15:10:06 首次发布

本文链接：https://blog.csdn.net/sq91fra/article/details/145160847

版权

持续更新中，最新版本可以查看语雀

笔记参考：

函数、极限与连续

函数

概念

函数是一种映射关系，它将一个集合中的每个元素（称为自变量）唯一地对应到另一个集合中的一个元素（称为因变量）。

定义域和值域：

定义域：函数中所有允许的输入值（自变量 x）的集合，表示函数在哪些输入值上有定义。
值域：函数所有可能的输出值（因变量 y）的集合，表示函数能够取到的所有结果。

常见函数的自然定义域❗

R表示全体实数

特殊函数

分段函数：在定义域不同的区间用不同的解析式表示的函数
隐函数：

抽象函数：

题型3，求抽象函数的定义域，例如：

题型4，求抽象函数的表达式：

函数的基本特性

有界性

单调性

奇偶性

周期性

反函数和复合函数

反函数

反函数性质：反函数和原函数关于直线关于直线y=x对称

反函数性质：反函数和原函数单调性相同

反函数性质：反函数和原函数奇偶性相同

复合函数

复合函数的性质：

复合函数f[g(x)] 中，f的定义域包含 g的值域

基本初等函数

常见的函数，一定要记住图像

幂函数

幂运算法则：

指数函数

对数函数

对数运算法则：

三角函数

拓展：

三角函数的关系：

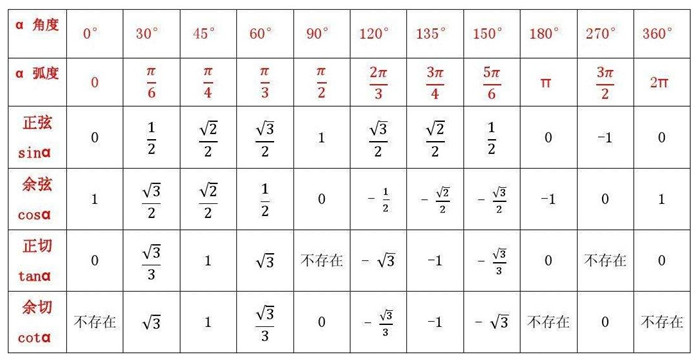
三角函数值表：

反三角函数

极限

无穷小：极限值为0

无穷大：极限值为无穷

数列的极限

收敛数列的性质：

夹逼准则：

题型，使用夹逼准则求数列极限：

函数的极限

概念

函数的极限就是自变量 x趋近于某个值 a时，函数 f(x)趋近于某个值 L。

极限关注的是函数在某一点附近的行为，不能理解极限为函数值域的最大值

数列极限和函数极限的区别和联系：

极限的运算法则

例题：

求极限的一种方法，直接带入法

极限的四则运算性质：

复合函数的极限运算法则：

因式分解求极限❗

根式有理化❗

思路：上下同时乘某式，消掉0因子

例题：

同除最大项❗

思路：上下同时除最大项，消掉无穷

两个重要极限❗

第一重要极限：

使用第一重要极限求极限

第二重要极限：

变式：

使用第二重要极限求极限：

函数的夹逼准则：

无穷小和无穷大

无穷小是函数，是趋近于0的过程
无穷大是函数，是趋近于无穷的过程

无穷小的性质

无穷小的和、差、积仍是无穷小
无穷小与有界函数的积是无穷小
无穷小的常数倍仍是无穷小
无穷小的极限为零

无穷小的比较

’

常用等价无穷小替换：

无穷小的运算法则

等价无穷小替换：
在求极限时，可以将复杂的无穷小替换为等价的简单无穷小。

例如：

连续

连续的定义

定理：

函数的间断点❗

间断点的分类：

示例：

基本初等函数的连续性

闭区间上的连续函数性质：

一定有最大值和最小值
零点定理：如果连续函数的一边大于0一边小于0，则函数的图像必定经过0
介值定理：零点定理的推论

导数

导数和可导

导数是函数在某一点的瞬时变化率，几何意义是函数在某一点的切线斜率

导数通过极限来定义，表示当自变量的变化量趋近于零时，函数的变化量与自变量变化量的比值的极限。导数的数学表达式如下：

导数的推论(可以不记)：

左导数和右导数：

当一个函数存在左导数和右导数且相等时，该函数可导

可导和连续的关系：可导函数必连续

连续 => 左导数=右导数 =>可导

导数性质

基本导数公式❗（第一块的最常考）：

导数的四则运算❗：

复合函数求导法则：

分段函数求导法则：两边正常求，中间求左右导数判断是否可导

反函数求导法则：反函数的导数等于原函数导数的倒数

隐函数求导法则：对隐函数方程两边同时对 x 求导，解出或y’

注意，y是x的函数，y对x求导是复合函数求导

参数函数求导法则：

幂指函数求导法则(对数求导法)

注意，(ln y)'对x求导是复合函数求导

求高阶导数：

求比其低一阶的导数
y’’ = (y’)‘，y’‘’ = (y’‘)’，…

例如：

微分

概念：函数在某点附近的微小变化的引起的改变量的近似值

导数和微分的关系：微分和导数密切相关，但微分更侧重于变化量的近似计算，而导数更侧重于变化率的描述

微分的运算法则：和导数的求导法则一致，只需将dx移到右边

微分在近似计算中的应用：

例如：

中值定理

罗尔中值定理

概念：

几何意义：某段连续且存在斜率的函数中，如果存在两点的函数值相等，那么两点中间至少有一点切线平行于x轴(斜率为0)

应用：

判断二元函数方程是否存在实根

拉格朗日中值定理

几何意义：某段连续且存在斜率的函数中，那么两点中间至少有一点的切线平行于ab(斜率相等)

洛必达法则

定理：

前提：

导数的应用

函数的单调性

定义：函数在某一区间的上升和下降的趋势

函数的导数和单调性的关系：

导数的几何含义为函数的斜率，因此：
- 导数为正数，单调递增
- 导数为负数，单调递减

函数凹凸性

定义：函数在某一区间是凹还是凸的

例如：

二阶导数的几何含义为函数的凹凸性，因此：
- 二阶导数为正数，凹
- 二阶导数为负数，凸

函数的极值和最值

极值是与它的两侧相比，大于两侧是极大值，小于两侧是极小值；最值则是函数在定义域或指定区间内的最大最小值

极值定理：

通过函数的导数的正负，可以判断函数单调性，从而取得极值
如果函数在某点附近可导，如果该点左侧单调递增，右侧单调递减，则函数在该点有极大值；如果该点左侧单调递减，右侧单调递增，则函数在该点有极小值

通过函数的一阶和二阶导数，可以判断函数的单调性和凹凸性，从而取得极值
如果函数在某点既不递增又不递减，且该点为凹或凸的中心点，则函数在该点有极值

具体如下：

函数曲线的渐近线

渐进线：

如果无定义点处的极限为无穷，则存在垂直渐近线
如果函数当 x 趋近于 ±∞ 时，极限为0，则存在水平渐近线

示例：

不定积分

概念

积分是导数的逆运算，分为定积分和不定积分两种。

其中，f(x)称为原函数

设原函数的导数为f(x)，那么f(x)的全体原函数称为f(x)的不定积分，记作：

例如：

C表示任意常数，常数的导数为0

不定积分的求解

公式

常用：

其他：

性质

第一类换元法(凑微分)

思路：

例如：

dx中，x可以任意加减常数，求出来的依然是全体原函数

第二类换元法

根式代换：设根式下面的东西为t，解出x=f(t)，代入原式，最后再将t用t=g(x)替换

示例：

三角代换：

根据公式消元：

示例：

分部积分法❗

公式：

示例：

定积分

概念

如何求一个任意图形的面积？

任何图形都可以分隔为多个曲边梯形

在一个特定区间 [a,b] 上对函数 f(x) 进行积分的过程
用于计算特定区间上的累积量或总和

牛顿莱布尼兹公式

示例：

性质

求解

换元积分法

定积分的换元法和不定积分的换元法类似，但是当变量代换后，积分上下限也要相应变换

第一积分换元法：

第二积分换元：

分部积分法

和不定积分的分部积分法类似

反常积分

无穷区间

无界函数

应用

几何应用

物理应用

常微分方程

微分方程概念

微分方程：包含未知函数及其导数(或微分)的方程
常微分方程：只含有一个自变量的微分方程
偏微分方程：含有多个自变量的微分方程
微分方程的阶：方程中出现的最高阶导数的阶数
线性微分方程：微分方程中指数幂都为1
微分方程的解：代入方程后使等式成立的函数
通解：含与方程阶数相等的任意常数的解
特解：通过初始条件确定通解中的常数后得到的唯一解
初始条件：题目给出来的条件

一阶微分方程

可分离变量的微分方程：可以将两个变量分离到等号两边的微分方程

求可分离变量的微分方程的通解：两边求不定积分

例如：

齐次方程

齐次方程：y/x同时出现的微分方程

例如下列微分方程都为齐次方程：

求齐次方程通解的三板斧：

使用三板斧化简后，两边求不定积分，最后将回代消掉u

例如：

一阶线性微分方程

概念:

一阶线性微分方程的形式：

当Q(x) = 0，称为 一阶齐次线性微分方程
当Q(x) != 0，称为 **一阶非齐次线性微分方程，**通解公式：

（要记住）

例如：

二阶常系数齐次线性微分方程

形如下图的微分方程称为二阶常系数线性微分方程

其中，当f(x) =0称为齐次，否则为非齐次

二阶常系数齐次线性微分方程的通解(要记住)：

多元函数微分法

形如 z = f(x,y)的函数称为二元函数

多元函数的极限

一元函数：
一元函数的定义域是函数f(x)在x轴上的投影
对于一元函数的极限，x轴所有方向只有左右，所以极限是左右逼近相等，则极限存在

二元函数
二元函数的定义域是函数f(x,y)在(x,y)面上的投影
对于二元函数的极限，(x,y)面所有方向是在该面上所有方向，所以极限是在(x,y)面上任意方向逼近(x0,y0)相等，则极限存在

一元函数求极限的方法在多元函数中依然适用，如两个重要极限，洛必达法则等

例如，判断二元函数极限不存在：

例如，使用重要极限求二元函数的极限：

偏导数

一元函数的导数：

定义：
几何意义：函数曲线在点(a,f(a))的斜率

多元函数的偏导数：

定义：
固定那个变量就是将该变量看作一个常数，将求一个二元函数的导数转换为求一元函数的导数
对x的偏导数可以理解为，只对x求导数，把y看作一个常数；对y求偏导同理。

几何意义：
x的偏导数：曲面在点(a,b)沿x轴方向的斜率
y的偏导数：曲面在点(a,b)沿y轴方向的斜率