整理一下这两天学的毒瘤玩意
二项式反演
若有
则有
因为
有一种应用是错排, fn 表示有n个是错排的方案, gn表示n个的总方案, 枚举有i个没有对上号, 就有
反演过后
除以一个 n! 算概率, 发现是 e ^ -1 的泰勒展开, 太神奇了
FFT
两个核心式子
然后就可以推了, 从下层把答案推到上层
分治FFT
先求出 [l - mid], 在用 [l - mid] 之间的 f 去卷 g, 贡献加到对 [mid+1 - r] 里面
泰勒展开
多项式求逆
求 B(x) 使
考虑倍增
若有 B'(x) 满足
当前的 B(x) 显然满足
相减, A(x) 显然不要
两边平方, 都乘A(x)
所以
多项式 ln
求 B(x) 满足
同时求导
对于后面那个求导
补充一个复合函数的求导(无关)
于是就是多项式求逆
多项式 exp
求
同时取对数
设
现在要求这个函数的 0 点
根据牛顿迭代
而
所以
根据玄学定理

每次从 G0 推到 G, n 可以扩大一倍, 于是就类似多项式求逆倍增就好










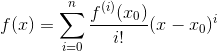















 1243
1243











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










