论文题目:Factorizing Personalized Markov Chains for Next-Basket Recommendation
Factorizing Personalized Markov Chains for Next-Basket Recommendation
矩阵分解(MF)和马尔可夫链(MC)是推荐系统常用的两种方法。矩阵分解通过将观测到的项目-用户矩阵进行分解模拟用户的喜好,而马尔科夫链通过观察用户近期的行为(关于项目的时间序列)来预测下一个时间点的行为。作者将这两种方法结合在了一起。对于每一个用户,我们需要学习其对应的一个转移矩阵,所以我们需要一个三维矩阵来记录这些信息。但是由于所观察到的这部分信息非常有限,我们用成对的交互模型来分解这个三维矩阵。为了学习模型的参数,我们引入了贝叶斯个性化排序的框架(详见论文阅读BPR)来处理数据。
这篇文章解决的问题中,每一个用户对项目的时间行为都是已知的,例如:用户的购买记录等。在这种情况下,同一时间可能会有很多不同的物品被购买,我们用“a set/basket”来定义这些物体。我们的任务就是给用户推荐下一次浏览网站时他想买的物品。
Contributions
1、我们引入了基于马尔可夫链的个性化转移矩阵,这使得我们可以同时捕捉时间信息和长期的用户喜好信息。
2、为了解决转移矩阵的稀疏问题,我们引入了矩阵分解模型,可以减少参数并改善表现结果。
3、我们的实验证明我们的模型表现优于其他基于时间序列信息的模型。
符号说明
同一时间,用户可能会买多个物品,这些物体的集合称为“一个 basket”。我们可以用下图来表示:
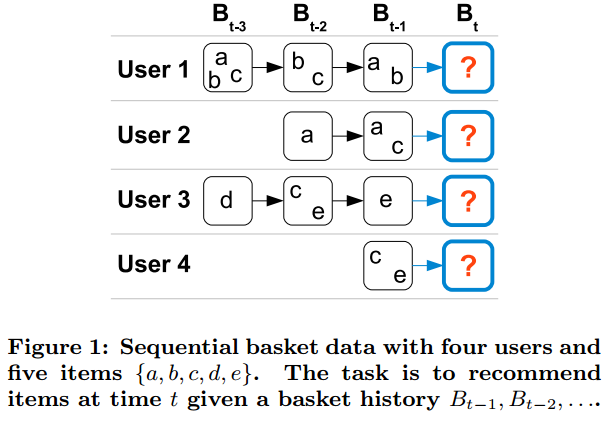
假设
U
为所有用户的集合,
项目推荐任务可以表述为用户
u
第
利用这个排名,我们可以为用户推荐排名前 n 的物体。
Factoring Personalized Markov Chains (FPMC)
Personalized Markov Chains for Sets
首先,我们介绍非个性化马尔可夫链的模型,然后运用最大似然估计(MLE)来求解参数,再将其扩展到个性化马尔科夫链。
Markov Chains for Sets
非个性化马尔可夫链模型即假设每一个用户的转移矩阵是相同的。而个性化推荐只是体现在将转移矩阵应用于用户的最后一次购买的物品,这些物体是不同的。
-
Xt,⋯,Xt−m
是变量,
xt,⋯,xt−m
是它们的实际取值,变量取值为所有的 basket
B
中的元素。因此,我们的状态空间的大小为
- 一个集合有n个元素,那么它的子集共有: C0n+C0n+C0n+⋯+C0n=2n
- 对于集合 R ,
|R| 指集合 R 中元素的个数。
显然,对于这么大的状态空间,马尔科夫链的长度不宜设置过长。为了简便,我们定义马尔可夫链的阶数
由于的状态空间的大小为 2|I| 且 m=1 ,因此转移矩阵的大小为 2|I|×2|I| 。可以看出,数据空间仍然很大,因此,我们对转移矩阵 A 做出以下修改。
我们先来通过下面的图有一个直观的理解。
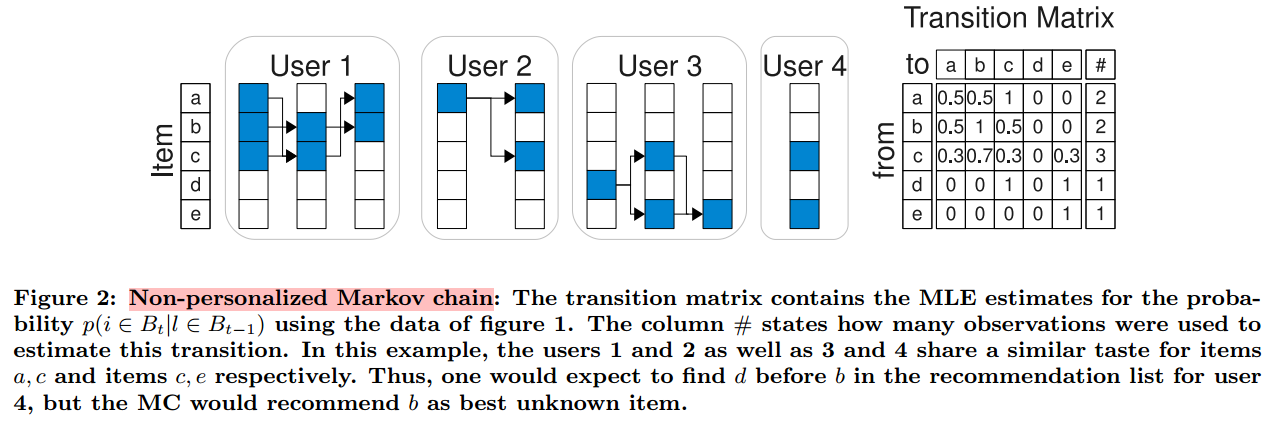
左边是我们将 Figure1 中的 basket 用
例如,第三行,计算的是,如果前一时刻买了物品c,那么下一时刻买不同的物品对应的概率是多少?我们可以使用的数据一共有三组,分别是: (a,b,c)→(b,c) 、 (b,c)→(a,b) 和 (c,e)→(e) 。计算下一时刻每个物体出现的次数,我们可以得到:
-
同理,我们可以得到转移矩阵
A
中其他元素的值。
得到了转移矩阵,我们就可以预测下一时刻用户想要购买各个物品的概率。例如,对于用户4,这一时刻购买的物品为 c、e,那么下一时刻购买各个物品概率为:
下面我们对此进行总结:
转移矩阵 A 记录的值不再是基于basket的转移概率,而是:
-
这样以来,状态空间的大小减小为
|I|
,转移矩阵的大小变为
|I|2
。
用最大似然估计计算 al,i 的值:
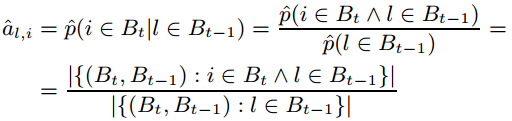
有了转移矩阵,当给出上一次的购买物品时,我们可以预测下一次购买物品 i 的概率为:
-
而我们之前提到的基于basket的完整的马尔可夫链可以表示为:
-
我们的目的只是找到最终的排序结果,对完整的马尔可夫链并不关心。
Personalized Markov Chains for Sets
目前为止,我们所说的马尔可夫链都是非个性化的。下面我们将其扩展到个性化:
则我们之前对转移矩阵的定义也发生变化:
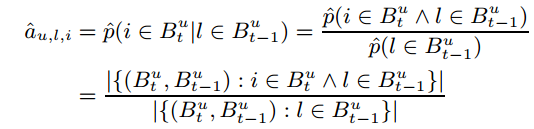
预测也发生变化:
-
这样意味着,每一个用户对应一个转移矩阵
Au
。最终我们得到一个三维矩阵
A∈[0,1]|U|×|I|×|I|
。
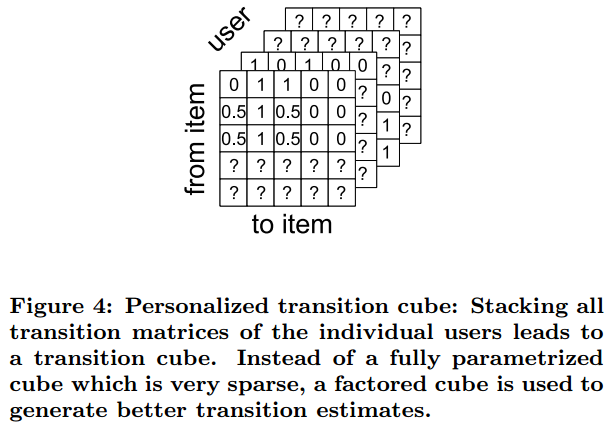
具体过程可以参考下图:
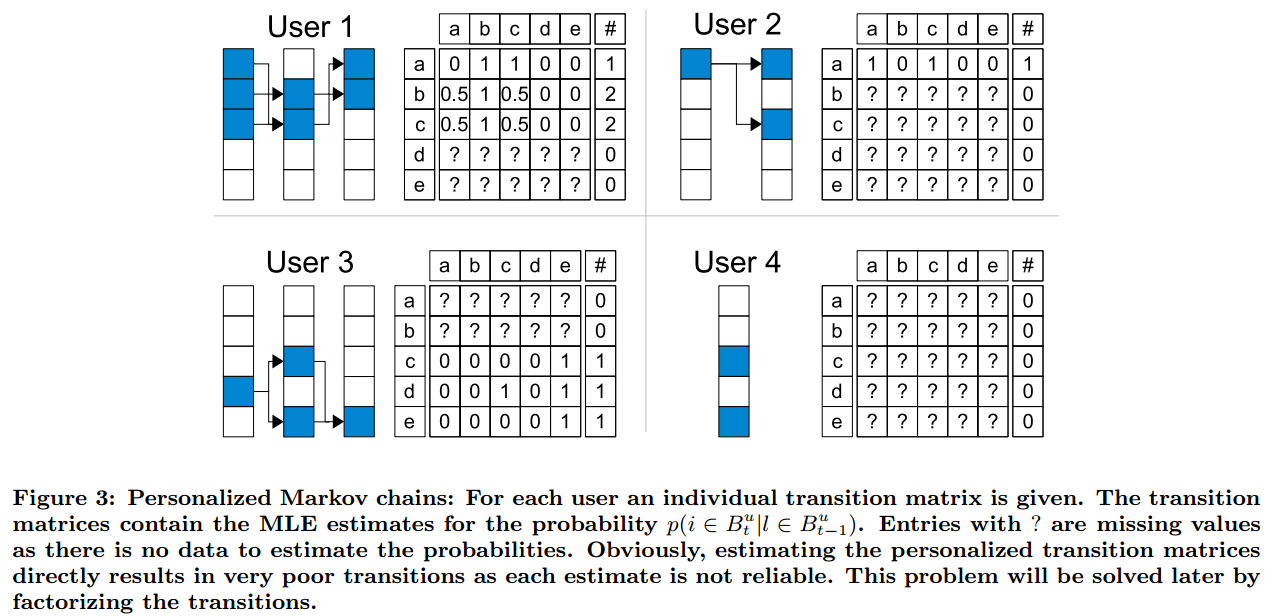
可以看出有很多缺失值,因为我们无法得到观测信息。而只通过一小部分信息来估计结果并不可靠。我们接下来会讨论这个问题并解决。
Limitations of MLE and Full Parametrization
个性化和非个性化马尔可夫链模型都或多或少存在不可靠问题,有两个原因:(1)它们处理的是完全参数化的转移图;(2)它们都应用MLE做估计。(1)意味着我们有
|U||I|2
或
|I|2
相互独立的参数,而应用MLE做出估计时,每一个参数的计算并没有考虑其他参数。例如,对
(l,j)
进行估计时,并没有考虑到
(l,i)
对其的影响;在个性化模型中更糟糕,因为甚至没有考虑到
(u′,l,j)
对
(u,l,j)
的影响。而对于(2),数据太少的情况下使用MLE可能会导致欠拟合。而我们的数据非常的稀疏,很容易失败。
因此,我们选择对转移三维矩阵进行矩阵分解,打破参数之间和估计时的独立性。这样就可以考虑到相似用户、项目,转移情况之间的相互影响。
Factorizing Transition Graphs
Factorization of the Transition Cube
我们用Tucker Composition
A^
来代替
A
:
可参考Tucker Composition、CP分解
其中,
C
为核张量(core tensor),
VU
为用户的特征矩阵,
VL
为上一时刻的项目的特征矩阵,
VI
为要预测的项目的特征矩阵。
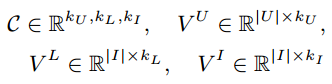
分解的维度分别是: kU,kL,kI 。我们设置 kU=kL=kI 。
由于我们观测到的转移矩阵 A 非常的稀疏,我们用下面的式子表示 U,I,L 两两之间的关系:
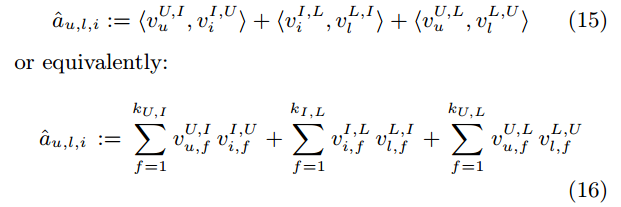
这样模型就直接模拟出三个矩阵因子之间的交互:
U
和

Factorization of the Transition Matrix
对于矩阵
A
,我们也可以进行上述分解:
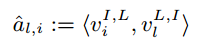
Summary of FPMC
上面我们得到的个性化马尔可夫链的预测结果为:
我们用 A^ 来建模 p(i∈But|But−1) :
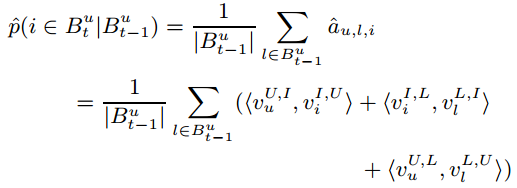
由于 (U,I) 和 L 之间是相互独立的,我们可以将其从求和符号中移出:
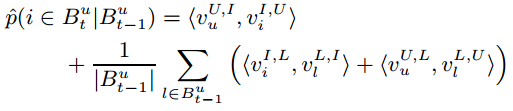
进行矩阵分解以后的模型与原来相比大大减少了参数。与之前的非个性化MC模型的
Item Recommendation From Sequential Set Data With FPMC
现在我们已经得到了FPMC模型(Factoring Personalized Markov Chains ),现在我们将其应用于推荐系统的任务上。我们引入S-BPR作为优化准则,并使用基于bootstrap sampling 的随机梯度算法求解我们的模型参数。(参考 论文阅读BPR)
Optimization Criterion S-BPR
推荐系统的任务就是获得项目的排名
>u,t
。为了给这些排名建模,我们假设一个预测器
x^:U×T×I→R
。
我们参考原始的 BPR 创建了关于时间序列的BPR——S-BPR(sequential BPR)。
我们定义:
在时间
t
用户
-
这里,我们的参数
Θ
为:
{VU,I,VI,U,VL,I,VI,L,VU,L,VL,U}
。
假设baskets之间和用户之间都是互相独立的,模型参数的最大后验(MAP)估计量:
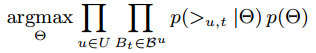
与 BPR 中的假设相同,我们可以将 p(Θ|>u,t) 写为:
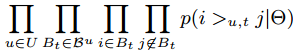
根据上面的定义 i>u,tj:⇔x^u,t,i>Rx^u,t,j ,我们得到:
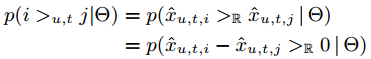
我们定义 p(z>0):=σ(z)=11+e−x :
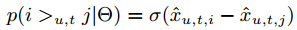
同时假设 θ∼N(0,1λθ)
我们得到SBPR的MAP为:
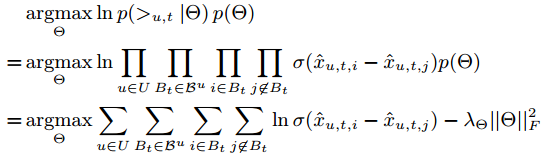
where λΘ is the regularization constant corresponding to σΘ 。
Item Recommendation with FPMC
我们 由FPMC得到的 x^ 为:
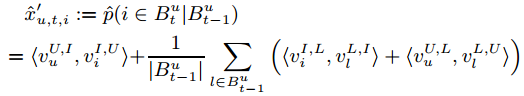
我们知道,因为要使用SBPR的优化标准,我们最终预测的是项目对
(i,j)
的排名先后
>u,t
,即
x^u,t,i−x^u,t,j
。
在FPMC模型中,
∑t∈But−1⟨vU,Lu,vL,Ul⟩
z这部分的信息来自于用户
u
,以及上一次买的物品
因此,我们可以简化上面的FPMC模型:
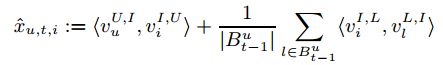
这样对结果并没有影响,因为:
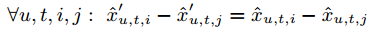
我们可以对比一下 FPMC(Factoring Personalized Markov Chains )、MF(Matrix Factorization)和FMC(Factorizing unpersonalized Markov chain)之间的关系:
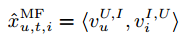
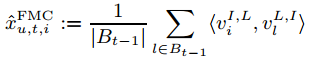
我们可以发现FPMC是MF和FMC的线性组合:
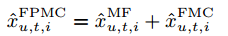
Learning Algorithm
论文使用LearnBPR的算法求解FPMC的参数,因为FPMC包含了MF和FMC,所以对于这两个模型LearnBPR也同样适用。(详见论文)
 2064
2064
 1057
1057
 1万+
1万+
 2201
2201

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?
































