机场停机位分配问题的精确和启发式求解方法

最新推荐文章于 2024-07-14 19:56:17 发布

安*东

最新推荐文章于 2024-07-14 19:56:17 发布

阅读量632

点赞数

文章标签：算法人工智能 python

本文链接：https://blog.csdn.net/strin__AAA/article/details/133701541

版权

问题定义

论文中的问题定义：机场有若干只停放国内航班的登机口（gate）、若干只停放国际航班的登机口以及一个可以停放国内/国际航班的停机坪(arpon).同时，机场有若干国内/国际航班需要被分配到登机口或停机坪上去，以满足机场运行。

论文中规定，所有航班的到达时间、起飞时间以及航班内乘客的人数等等都是固定的、静态的。当一架航班根据其到达时间到达机场，此时分配给该航班的登机口必须是可用，并且直到该航班的起飞时间登机口才允许被其他航班占用。

此外，每架航班上的乘客类型有：离场乘客，中转乘客和登机乘客。其中离场乘客和登机乘客称为非中转乘客。非中转乘客的步行距离仅由航班分配的登机口决定，中转乘客的步行距离由其换成航班分配的登机口和当前航班分配的登机口决定。

每个登机口/停机坪都有一个表，里面记录了当前登机口/停机坪到其他登机口以及机场出入口的距离。

论文解决的问题是在最小化分配到停机坪的航班数量的前提下，最小化总乘客步行距离。

求分配给停机坪的最少飞机数量

相关参数： $NA_{D}^{*}$ 表示分配到国内登机口的最大航班数量， $NA_{I}^{*}$ 表示分配到国际登机口的最大航班数量， $NA^{*}$ = n - $NA_{D}^{*}$ - $NA_{I}^{*}$ 表示分配到停机坪的最小航班数量。 $NA_{D}^{*}$ 和 $NA_{I}^{*}$ 可以独立求解，因为国内航班和国际航班分别在不同的航站楼停放。

论文中采用的是最大成本网络流模型。

构建网络（有向图）

求解 $NA_{D}^{*}$ ，如图1所示，其中节点代表国内飞机，节点之间的弧代表航班之间不重叠。弧的编号代表机位编号。

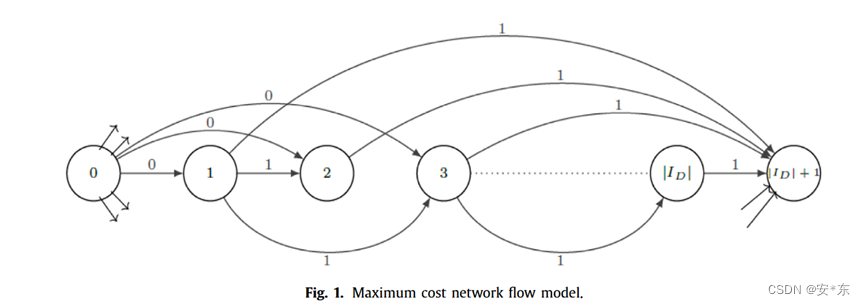该网络具有从节点 0 出发的 | $I_{D}$ |+1 条弧，一端到代表每架国内航班的节点，一端到终端节点 | $I_{D}$ |+1。有 | $I_{D}$ |+1 条弧到达终端节点 | $I_{D}$ |+1，其中一端来自白标每架国内航班的节点，一端来自源节点（节点 0）。如果对应的国内航班不重叠，则两个节点之间存在弧。所有弧权重均为 1。其中 $I_{D}$ 表示所有国内航班集合,| $I_{D}$ |表示 $I_{D}$ 的数量。

举个例子：让 $I_{D}$ = 4，且航班1与2、4在时间上不冲突，2与4也不冲突，3与4也不冲突。则如图所示：其中蓝色的线表示从节点0出的发的弧，绿色的线表示从其他节点出发到终端节点5的弧。弧（1，2）、弧（1，4），弧（2，4），弧（3，4）分别表示航班1与2、4在时间上不冲突，2与4也不冲突，3与4也不冲突。

求解最大流网络模型

我们从节点 0 向节点 | $I_{D}$ |+1 发送 | $K_{D}$ |-1 单位的流量，以便最大化访问的弧数。从节点0到节点| $I_{D}$ |+1的最大成本值给出了可以分配给| $K_{D}$ |−1个登机口的国内飞机的最大数量。 $K_{D}$ 表示国内航站楼的所有登机口。

最大成本网络流问题（Maximum Cost Network Flow Problem）是网络流问题的一种变体，其中在网络中的边（或弧）上有相关的成本（或费用）与流量相关。问题的目标是在给定网络中找到一种从源节点到汇节点的流动分配方式，使得总成本最大化。

最大成本网络流问题（Maximum Cost Network Flow Problem）是一个组合优化问题，其目标是在网络中找到一种从源节点到汇节点的流动分配方式，使得总成本最大化。这类问题可以通过一些经典的算法和方法来求解。以下是最大成本网络流问题的一些常见解法：

1. 最小费用最大流算法（Minimum Cost Maximum Flow Algorithm）：
最小费用最大流算法是一种经典的解决网络流问题的算法，它可以被用来解决最大成本网络流问题。该算法基于网络中的最短路径思想，通过在残余图上寻找最短路径来不断调整流量，直到无法找到更短的路径为止。算法包括以下步骤：
- 使用最短路径算法（例如Dijkstra算法或Bellman-Ford算法）寻找从源节点到汇节点的最短路径。
- 在最短路径上增加流量，同时更新路径上的边的成本。
- 重复以上步骤，直到无法找到更短的路径为止。

2. 成功流（Successive Shortest Path）算法：
成功流算法是一种改进的最小费用最大流算法，它使用了负费用圈（Negative Cost Cycle）的概念。该算法通过不断找负费用圈来增加流量，并且可以保证在有负费用圈的情况下仍然能够找到最优解。

3. 拉贝尔改进算法（Label-Correcting Algorithm）：
拉贝尔改进算法是一种广泛用于网络流问题的启发式算法。它基于Bellman-Ford算法，通过在图上向前、向后扩展标号以及负费用弧的检测来不断改进流的分配，直到找到最优解。

4. 费用缩放算法（Cost Scaling Algorithm）：
费用缩放算法是一种基于网络流问题中成本的范围的启发式算法。该算法通过逐渐缩小成本范围，将问题转化为一系列相对较小范围的问题，从而加速问题的求解过程。

5. 线性规划和整数规划求解器：
最大成本网络流问题也可以被建模为线性规划或整数规划问题，然后使用现成的线性规划或整数规划求解器（例如LP或MIP求解器）进行求解。

论文中的模型数学描述：

$A_{D}$ ：代表最大成本网络上的国内飞机的一组弧

$z_{ij}$ : 1 选择弧（i，j）；0 其他

目标： $Max Z_{D} = \sum_{(i,j)\epsilon A_{D}}^{} z_{ij}$

约束条件：

（1） $\sum_{(0,j)\epsilon A_{D}}^{}z_{0j}\leq |K_{D}| - 1$

（2） $\sum_{(i,|I_{D}|+1)\epsilon A_{D}}^{}z_{i(|I_{D}|+1)}\leq|K_{D}|-1$

（3） $\sum_{(i,j)\epsilon A_{D} }z_{ij} = \sum_{(j,i)\epsilon A_{D}}z_{ij} ,i = 1,...,|I_{D}|$

（4） $\sum_{(i,j)\epsilon A_{D}}z_{ij}\leq 1 , i = 1,...,|I_{D}|$

模型的最优目标函数值 $Z_{D}^{*}$ 为国内所有登机口可分配的最大国内航班数量， $NA_{D}^{*} = |I_{D}| - Z_{D}^{*}$ 为停机坪上国内航班的最少数量。论文中采用LP算法在多项式时间内求解 $Z_{D}^{*}$ 。国际航班同理即可求解。

分支定界（B&B）、波束搜索(BS)和过滤波束搜索(FBS)算法

论文中按照距机场出入口距离的非递减顺序对除停机坪之外的国内（国际）登机口进行索引。因此，1号登机口（| $K_{D}$ |）是距离机场出入口最近的国内（国际）登机口，m+1号登机口（即停机坪）是距离机场出入口最远的登机口。航班按其到达机场的非递增顺序进行索引。

分支定界（B&B）

B&B树最多有n层，每层最多有m+1个节点。树的第 i 层代表飞机 i 的分配。第 i 层的节点 k 用于将飞机 i 分配到 k 登机口。不创建代表不可行分配的节点。 B&B算法采用深度优先策略。其中，n表示所有航班数量，m表示所有登机口的数量。

在任何级别，它都会选择总加权步行距离值下限最小的节点，并继续执行后续级别。如果某一级别的所有节点都被评估或丢弃，我们将回溯到上一个级别。每当达到级别 0 时我们就会终止。

波束搜索(BS)和过滤波束搜索(FBS)

BS 和 FBS 树最多有 n 层，其中树的第 i 层代表飞机 i 的分配。BS 算法通过总步行距离值的下限来评估节点，并在有希望的节点中选择最具吸引力的波束宽度节点以进行进一步分支，同时永久丢弃其余节点。FBS算法分两步在有希望的节点中选择最有吸引力的节点：首先，算法根据现实的步行距离评估节点，并选择最大过滤器宽度的有希望的节点进行进一步评估，丢弃其余的。其次，根据总步行距离的下限进一步评估所选节点；选择最具吸引力的波束宽度节点进行进一步分支，而其余节点则被删除。

有希望的节点：如果一个节点没有被我们的消除规则丢弃，如果它没有进行比初始上限更多的停机坪分配，并且如果它的下限小于初始上限，我们称该节点为有希望的。即当初始上限不是停机坪可行时（即不进行最小数量的停机坪分配），我们允许违反约束 $\sum_{i\epsilon I}^{}x_{im+1} = NA^{*}$ ,其中， $x_{im+1}$ 是一个决策变量，表示是否将航班i分配到停机坪。