(一)认识回归
回归是统计学中最有力的工具之一。机器学习监督学习算法分为分类算法和回归算法两种,其实就是根据类别标签分布类型为离散型、连续性而定义的。顾名思义,分类算法用于离散型分布预测,如前面讲过的KNN、决策树、朴素贝叶斯、adaboost、SVM、Logistic回归都是分类算法;回归算法用于连续型分布预测,针对的是数值型的样本,使用回归,可以在给定输入的时候预测出一个数值,这是对分类方法的提升,因为这样可以预测连续型数据而不仅仅是离散的类别标签。
回归的目的就是建立一个回归方程用来预测目标值,回归的求解就是求这个回归方程的回归系数。预测的方法当然十分简单,回归系数乘以输入值再全部相加就得到了预测值。
1,回归的定义
回归最简单的定义是,给出一个点集D,用一个函数去拟合这个点集,并且使得点集与拟合函数间的误差最小,如果这个函数曲线是一条直线,那就被称为线性回归,如果曲线是一条二次曲线,就被称为二次回归。
2,多元线性回归
假定预测值与样本特征间的函数关系是线性的,回归分析的任务,就在于根据样本X和Y的观察值,去估计函数h,寻求变量之间近似的函数关系。定义:
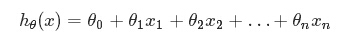
其中,n = 特征数目;
x j = 每个训练样本第j个特征的值,可以认为是特征向量中的第j个值。
为了方便,记x0= 1,则多变量线性回归可以记为:
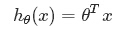
Note:注意多元和多次是两个不同的概念,“多元”指方程有多个参数,“多次”指的是方程中参数的最高次幂。多元线性方程是假设预测值y与样本所有特征值符合一个多元一次线性方程。
3,广义线性回归
用广义的线性函数:
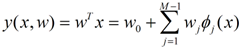
wj是系数,w就是这个系数组成的向量,它影响着不同维度的Φj(x)在回归函数中的影响度,Φ(x)是可以换成不同的函数,这样的模型我们认为是广义线性模型,Φ(x)=x时就是多元线性回归模型。
(二)线性回归的求解
说到回归,常常指的也就是线性回归,因此本文阐述的就是多元线性回归方程的求解。假设有连续型值标签(标签值分布为Y)的样本,有X={x1,x2,...,xn}个特征,回归就是求解回归系数θ=θ0, θ 1 ,…, θ n 。那么,手里有一些X和对应的Y,怎样才能找到θ呢? 在回归方程里,求得特征对应的最佳回归系数的方法是最小化误差的平方和。这里的误差是指预测y值和真实y值之间的差值,使用该误差的简单累加将使得正差值和负差值相互抵消,所以采用平方误差(最小二乘法)。平方误差可以写做:
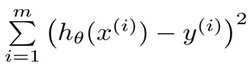
至于为何采用最小误差平方和来求解,其统计学原理可参考“对线性回归、逻辑回归、各种回归的概念学习”的“深入线性回归”一节。
在数学上,求解过程就转化为求一组θ值使求上式取到最小值,那么求解方法有梯度下降法、








 本文详细介绍了线性回归算法,包括回归的定义、多元线性回归和广义线性回归。线性回归的求解方法涵盖梯度下降法、Normal Equation、局部加权线性回归以及岭回归。还探讨了模型性能度量和Python实现,并提供了模型调优的建议。
本文详细介绍了线性回归算法,包括回归的定义、多元线性回归和广义线性回归。线性回归的求解方法涵盖梯度下降法、Normal Equation、局部加权线性回归以及岭回归。还探讨了模型性能度量和Python实现,并提供了模型调优的建议。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








