核函数
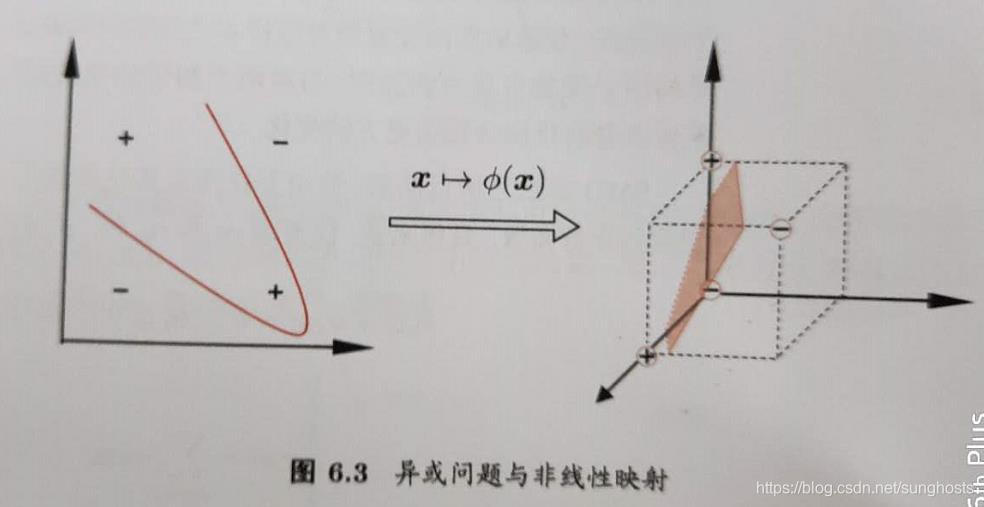
异或问题不是线性可分的,对这样的问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。
令 ϕ ( x ) \phi(x) ϕ(x) 表示将 x x x 映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
f ( x ) = w T ϕ ( x ) + b f(x)=w^T \phi(x) + b f(x)=wTϕ(x)+b
类似上篇博客提到的对偶问题,映射后的公式如下:
m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ϕ ( x i ) T ϕ ( x j ) max_{\alpha} \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \phi(x_i)^T \phi(x_j) maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕ(xi)Tϕ(xj) 公式(1)
s . t . ∑ i = 1 m α i y i = 0 , α i ≥ 0 s.t. \quad \sum_{i=1}^m \alpha_i y_i =0 , \alpha_i \ge 0 s.t.i=1∑mαiyi=0,αi≥0
求解公式(1)涉及到 ϕ ( x i ) T ϕ ( x j ) \phi(x_i)^T \phi(x_j) ϕ(xi)Tϕ(xj) 的内积运算,这是样本在映射到特征空间之后的内积。如果维数很大,计算是很困难的。可以设想这样一个函数(称为核技巧):
κ ( x i , x j ) = ϕ ( x i ) T ϕ ( x j ) \kappa(x_i, x_j) = \phi(x_i)^T \phi(x_j) κ(xi,xj)=ϕ(xi)Tϕ(xj)
即 x i x_i xi 和 x j x_j xj 在特征空间的内积等于它们在原始样本空间中通过函数 κ ( . , . ) \kappa(.,.) κ(.,.) 计算的结果。有这样的函数,上式可重写为:
m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j κ ( x i , x j ) max_{\alpha} \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \kappa(x_i, x_j) maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjκ(xi,xj) 公式(2)
s . t . ∑ i = 1 m α i y i = 0 , α i ≥ 0 s.t. \quad \sum_{i=1}^m \alpha_i y_i =0 , \alpha_i \ge 0 s.t.i=1∑mαiyi=0,αi≥0
求解后可得到:
f ( x ) = w T + b = ∑ i = 1 m α i y i ϕ ( x i ) T ϕ ( x j ) + b = ∑ i = 1 m α i y i κ ( x i , x j ) + b f(x)=w^T+b=\sum_{i=1}^m \alpha_i y_i \phi(x_i)^T \phi(x_j) +b=\sum_{i=1}^m \alpha_i y_i \kappa(x_i, x_j) + b f(x)=wT+b=i=1∑mαiyiϕ(xi)Tϕ(xj)+b=i=1∑mαiyiκ(xi,xj)+b 公式(3)
这里的函数 κ ( . , . ) \kappa(.,.) κ(.,.) 就是核函数,公式(3)表示模型最优解可通过训练样本的核函数展开,这一展式也称支持向量展式。
如果知道 ϕ ( . ) \phi(.) ϕ(.) 的具体形式,则可以写出核函数 κ ( . , . ) \kappa(.,.) κ(.,.) ,但现实任务中通常不知道 ϕ \phi ϕ 是什么形式,那么合适的核函数是否一定存在?什么样的函数适合做核函数?
定理:核函数
令 χ \chi χ 为输入空间, κ ( . , . ) \kappa(.,.) κ(.,.) 是定义在 χ × χ \chi \times \chi χ×χ 上的对称函数,则 κ \kappa κ 是核函数当且仅当对于任意数据 D = x 1 , x 2 , . . . , x m D = {x_1,x_2,...,x_m} D=x1,x2,...,xm ,核矩阵 K 总是半正定的:
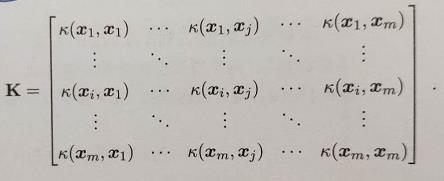
上述定理表明,只要一个对称函数所对应的核矩阵半正定,就能作为核函数。任何一个核函数都隐式地定义了一个称为“再生核希尔伯特空间(RKHS)”的特征空间。
自己去找一个核函数还是很难的,怎么办呢?还好牛人们已经帮我们找到了很多的核函数,而常用的核函数也仅仅只有那么几个。下面我们来看看常见的核函数, 选择这几个核函数介绍是因为scikit-learn中默认可选的就是下面几个核函数。
| 名称 | 表达式 | 参数 |
|---|---|---|
| 线性核 | κ ( x i , x j ) = x i T x j \kappa(x_i,x_j)=x_i^T x_j κ(xi,xj)=xiTxj | |
| 多项式核 | κ ( x i , x j ) = ( x i T x j ) d \kappa(x_i,x_j)=(x_i^T x_j)^d κ(xi,xj)=(xiTxj)d | d ≥ 1 d \ge 1 d≥1是多项式的次数 |
| 高斯核 | $\kappa(x_i,x_j)=exp(-\frac{ | |
| Sigmoid核 | κ ( x i , x j ) = t a n h ( β x i T x j + θ ) \kappa(x_i,x_j)=tanh(\beta x_i^T x_j + \theta) κ(xi,xj)=tanh(βxiTxj+θ) | t a n h tanh tanh为双曲正切函数( β > 0 , θ < 0 \beta \gt 0,\theta \lt 0 β>0,θ<0) |
线性可分SVM我们可以和线性不可分SVM归为一类,区别仅仅在于线性可分SVM用的是线性核函数。
高斯核函数(Gaussian Kernel),在SVM中也称为径向基核函数(Radial Basis Function,RBF),它是非线性分类SVM最主流的核函数。libsvm默认的核函数就是它。
对文本分类通常采用线性核,情况不明时,可以尝试高斯核。
此外,核函数还可以通过组合得到,如 κ 1 \kappa_1 κ1 和 κ 2 \kappa_2 κ2 是核函数,那么下面的组合也是核函数
γ 1 κ 1 + γ 2 κ 2 \gamma_1 \kappa_1 + \gamma_2 \kappa_2 γ1κ1+γ2κ2
κ 1 ⨂ κ 2 ( x , z ) = κ 1 ( x , z ) κ 2 ( x , z ) \kappa_1 \bigotimes \kappa_2(x,z)=\kappa_1(x,z) \kappa_2(x,z) κ1⨂κ2(x,z)=κ1(x,z)κ2(x,z)
κ ( x , z ) = g ( x ) κ 1 ( x , z ) g ( z ) \kappa(x,z) =g(x) \kappa_1(x,z) g(z) κ(x,z)=g(x)κ1(x,z)g(z)
参考
周志华《机器学习》
https://www.cnblogs.com/pinard/p/6103615.html
李航《统计学习方法》





















 4万+
4万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








