高等数学

#第二章：导数与微分
##第六节 隐函数的导数 由参数方程所确定的函数的导数 相关变化率
###1、隐函数的导数
显函数： $y=\sqrt[3]{11-x}$；
隐函数： $x+y^3-1=0$;
隐函数显化:将$x+y^3-1=0$转换成$y=\sqrt[3]{1-x}$

##多元函数的基本概念
在很多自然现象以及实际的问题中，经常会遇到多个变量之间的依赖关系，如圆柱体的体积$V$和它的半径$r$ 、高$h$之间具有关系：$$V=\pi r^{2}h$$
这里，当$r,h$在集合 { ( r , h ) ∣ r > 0 , h > 0 } \{(r,h)|r>0,h>0\} {(r,h)∣r>0,h>0} 内，取定一对值$(r,h)$时， $V$的对应值就随之确定。
二元函数：
设$D$ 是$R^2$的一个非空子集，称映射$f:D\to R$ 为定义在$D$上的一个二元函数，通常记为：$$z=f(x,y),(x,y)\in D$$
其中点集$D$称为该函数的定义域， $(x,y)$称为自变量， $z$称为因变量，
偏导数：
1）引用偏导数的目的是研究函数的变化率；
2）设二元函数$z=f(x,y)$在点$(x_0,y_0)$的某一邻域内有定义，当 $y$固定在$y_0$而$x$在$x_0$处有增量$\Delta x$ 时，相应的函数就有增量$f(x_0+\Delta x,y_0)-f(x_0,y_0)$，
如果$$\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}$$
存在，则称此极限为函数$z=f(x,y)$在点$(x_0,y_0)$处对$x$的偏导数，记作：$${\frac{\partial z}{\partial x}|}_{x=x_{0}y=y_0},{\frac{\partial f}{\partial x}|}_{x=x_{0}y=y_0},f_x(x_0,y_0)$$

如果函数$z=f(x,y)$在区域$D$内每一个点 处对 的偏导数都存在，那么这个偏导数就是$x,y$的函数，它就称为函数$z=f(x,y)$对自变量$x$的偏导数，记作：$$\frac{\partial z}{\partial x},\frac{\partial f}{\partial x},z_x,f_x(x,y)$$

###多元函数的极值及其求法
极值的定义：
设函数$z=f(x,y)$的定义域$D$，$P_0(x_0,y_0)$为$D$的内点，若存在着$P_0$的某个邻域$U(P_0)\subset D$ ，使得对于该邻域内异于$P_0$的任何点$(x,y)$都有$f(x,y)<f(x_0,y_0)$ ，则称函数$f(x,y)$在点$P_0(x_0,y_0)$有极大值$f(x_0,y_0)$ ，点$P_0(x_0,y_0)$称为函数$f(x,y)$ 的极大值点。
定理1（必要条件）：
设函数$z=f(x,y)$在点$(x_0,y_0)$具有偏导数，且在点 $(x_0,y_0)$处有极值，则有：$$f_x(x_0,y_0)=0,f_y(x_0,y_0)=0$$
定理2（充分条件）：
设函数$z=f(x,y)$在点$(x_0,y_0)$的某邻域内连续且有一阶及二阶连续导数，且$f_x(x_0,y_0)=0,f_y(x_0,y_0)=0$ ，令：$f_{x}x(x_0,y_0)=A,f_{x}y(x_0,y_0)=B,f_{y}y(x_0,y_0)=C$，
则函数$z=f(x,y)$在点$(x_0,y_0)$处是否取得极值的条件如下：
（1）$AC-B^2>0$ 时具有极值，且当$A<0$时有极大值，当$A>0$时有极小值；
（2）$AC-B^2<0$ 时没有极值；
（3）$AC-B^2=0$ 时可能有极值，也可能没有极值，需要另外讨论
拉格朗日乘法:
寻求函数$z=f(x,y)$在条件$\varphi (x,y)=0$下的可能极值点，先做拉格朗日函数：$$L(x,y)=f(x,y)+\lambda \varphi (x,y)$$
其中$\lambda$是拉格朗日乘子，为常数；
建立方程组：
$$\{\begin{array}{l}{f}_x(x,y)+\lambda {\varphi }_x(x,y)=0,\\ f_y(x,y)+\lambda {\varphi }_y(x,y)=0,\\ \varphi (x,y)=0,\end{array}$$
由方程组解出的$x,y,\lambda$ ，可能就是我们需找的在附加条件下的极值点

##方向导数与梯度：
1.背景：
偏导数反映的是函数沿着坐标轴方向的变化率，但是许多物理现象告诉我们，变化率的方向是任意的，比如：热空气要向冷的地方流动，气象学中就要确定大气温度、气压沿着某些方向的变化率，因此，我们来讨论函数沿着任一指定方向的变化率问题。
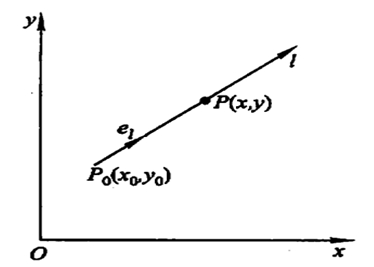
2.概念：
设$l$是$xOy$平面上以$P_0(x_0,y_0)$为始点的一条射线，$e_l=(cos\alpha ,cos\beta )$ 是与$l$同方向的单位向量，射线$l$的参数方程为：$$\begin{gathered} x=x_0+tcos\alpha \\ y=y_0+tcos\beta \\ (t>=0) \end{gathered}$$

若以下表达式成立，则称此极限为函数$f(x,y)$在点$P_0$沿方向$l$ 的方向导数，记作${\frac{\partial f}{\partial l}|}_{x_0,y_0}$ ，即： $${\frac{\partial f}{\partial l}|}_{x_0,y_0}=\underset{t\to 0^{+}}{\lim }\frac{f(x_0+tcos\alpha ,y_0+tcos\beta )-f(x_0,y_0)}{t}$$
3.定理：
如果函数$f(x,y)$在点$P_0$可微分，那么函数在该点任意一方向$l$的方向导数存在，且有： $${\frac{\partial f}{\partial l}|}_{x_0,y_0}=\underset{t\to 0^{+}}{\lim }\frac{f(x_0+tcos\alpha ,y_0+tcos\beta )-f(x_0,y_0)}{t}$$
其中，$cos\alpha ,cos\beta$是方向$l$的方向余弦。
4.意义：
从方向导数的意义可以知道，方向导数就是函数$f(x,y)$在点$P_0(x_0,y_0)$处沿方向$l$的变化率。

【例】
求函数 在点 处沿从点 到点 的方向导数。
解：这里的方向 即向量 的方向，与 同向的单位向量为

因为函数可以微分，且

故所求方向导数为：

梯度
1.定义
设函数$f(x,y)$在平面区域$D$内具有一阶连续偏导数，且对于每一个点$P_0(x_0,y_0)\in D$，都可定出一个向量$f_x(x_0,y_0)\vec{i}+f_y(x_0,y_0)\vec{j}$
这个向量称为函数$f(x,y)$在点$P_0(x_0,y_0)$的***梯度***，记作$gradf(x_0,y_0)$或者$\nabla f(x_0,y_0)$ ，即$$gradf(x_0,y_0)=\nabla f(x_0,y_0)=f_x(x_0,y_0)\vec{i}+f_y(x_0,y_0)\vec{j}$$
其中$\nabla=\frac{{\partial }}{{\partial }x}\vec{i} +\frac{{\partial }}{{\partial }y}\vec{j} $，称为（二维的）\ast \ast \ast 向量微分算子\ast \ast \ast ，2.应用1-计算方向导数：如果函数$f(x,y)$ 在点$P_0(x_0,y_0)$ 可微分， $e_l=cos\alpha +cos\beta$是与$l$同方向的单位向量，则方向导数：
$${\frac{\partial f}{\partial l}|}_{x_0,y_0}=f_x(x_0,y_0)cos\alpha +f_y(x_0,y_0)cos\beta =gradf(x_0,y_0)\times \overrightarrow{e_l}=|grad(f(x,y))|cos\theta$$
其中 $\theta =(gradf(x_0,y_0),\overrightarrow{e_l})$方向夹角
从上面的表达式中，可以看出函数在一点的梯度与其对应的方向导数之间的关系，
（1）当$\theta =0$ ，即$\overrightarrow{e_l}$与梯度$gradf(x_0,y_0)$方向相同时，函数$f(x,y)$增加最快。
（2）当$\theta =\pi$ ，即$\overrightarrow{e_l}$与梯度$gradf(x_0,y_0)$方向相反时，函数$f(x,y)$减少最快。
（3）当$\theta =\pi /2$，即$\overrightarrow{e_l}$与梯度$gradf(x_0,y_0)$方向正交时，函数$f(x,y)$变化率为0。