1 Introduction
随机梯度下降的更新流程为
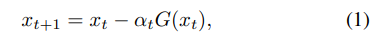
其中
x
∈
R
n
x\in \mathbb{R}^n
x∈Rn为模型参数,我们可以给定包含
P
P
P个工作节点的集群来加快训练的过程,其中第
p
p
p个节点计算得到的更新为
G
p
(
x
t
)
G^p(x_t)
Gp(xt),更新过程修改为
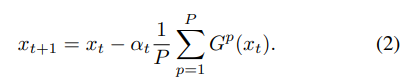
这种同步的随机梯度下降算法称为S-SGD.理想情况下训练的速度可以加快了P倍,但由于受到通信条件的限制,并不能实现这么高的速度,因此提出了梯度稀疏化来加快通信过程,更新过程修改为
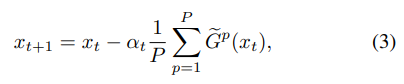
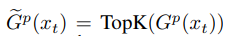
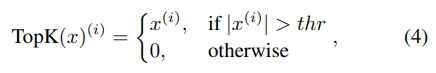
考虑到不同节点的非零元素坐标可能是不一样的,因此在聚合的时候通信复杂度为
O
(
k
P
)
O(kP)
O(kP).如今有一种新的稀疏化算法称为gTop-
k
k
k,可以将通信复杂度下降到
O
(
k
l
o
g
P
)
O(klog\ P)
O(klog P).
2 gTop- k k k算法
在介绍算法前,我们首先进行一些定义,令
v
t
v_t
vt为每个节点本地模型,
ϵ
t
p
\epsilon^p_t
ϵtp为节点
p
p
p在
t
t
t次迭代时本地梯度残差,在任何一次迭代中,每个节点都拥有相同的模型.gTop-
k
k
k算法更新流程为:
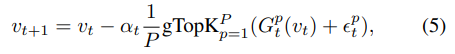
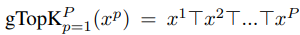
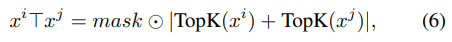
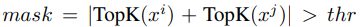
t
h
r
thr
thr为两个稀疏化向量相加后第
k
k
k大的绝对值,并同时生成一个
g
M
a
s
k
p
gMask^p
gMaskp向量
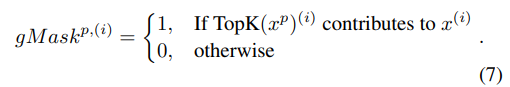
具体的算法流程为

并且我们定义一个辅助向量
x
t
x_t
xt
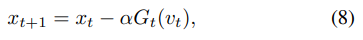
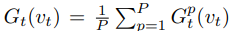

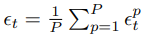
3 收敛分析
3.1 定义和假设
我们假设所有的工作节点都有完整的数据副本,并且优化的函数
f
f
f是一个非凸函数,有
L
L
L-平滑性,
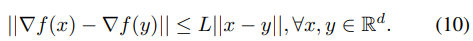
其中计算的随机梯度是无偏的,即
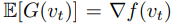
并且定义梯度平方的上限
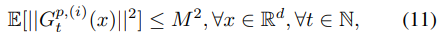
其中
G
t
p
,
(
i
)
(
x
)
G^{p,(i)}_t(x)
Gtp,(i)(x)为批量大小为
b
b
b的数据中第
i
i
i个样本计算的梯度,P个工作节点的总数据量为
B
=
P
b
B=Pb
B=Pb.我们设置
G
t
p
(
x
)
=
1
b
∑
i
=
1
b
G
t
p
,
(
i
)
(
x
)
G^p_t(x)=\frac{1}{b}\sum_{i=1}^bG^{p,(i)}_t(x)
Gtp(x)=b1i=1∑bGtp,(i)(x)
因此我们可以得到
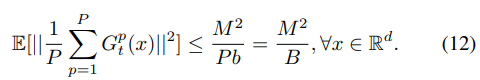

证明的主要思路为:
- 首先限定没有经过稀疏化的模型 x t x_t xt和稀疏化后的模型 v t v_t vt之间的差距,它使我们能够限制 f f f的梯度的期望平方和,从而确保收敛.
- 我们将 f f f的期望均方梯度与一些足够的条件绑定在一起,以得出收敛速度。
3.2 主要结果
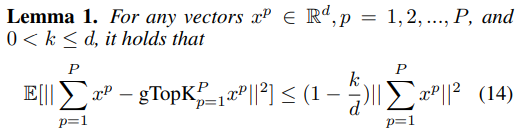
证明:对于向量
x
∈
R
n
x\in \mathbb{R}^n
x∈Rn,有
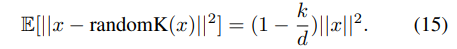
将其于假设1结合得证
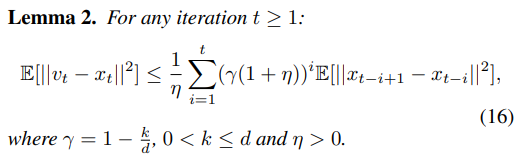
证明:我们可以推导出
v
t
+
1
v_{t+1}
vt+1和
x
t
+
1
x_{t+1}
xt+1之间的差别,即
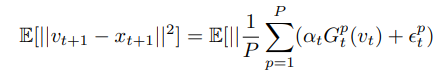

倒数第二个不等式是由于
∣
∣
a
+
b
∣
∣
2
≤
(
1
+
γ
)
∣
∣
a
∣
∣
2
+
(
1
+
γ
(
−
1
)
)
∣
∣
b
∣
∣
2
||\mathbf{a}+\mathbf{b}||^2\le (1+\gamma)||\mathbf{a}||^2+(1+\gamma^{(-1)})||\mathbf{b}||^2
∣∣a+b∣∣2≤(1+γ)∣∣a∣∣2+(1+γ(−1))∣∣b∣∣2,将上述不等式从i=0到t进行迭代可以得到:
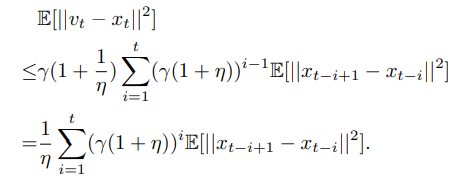
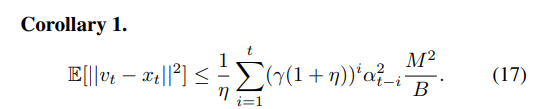
证明:结合上述的Lemma 2和公式(12),我们可以得到:


证明:考虑到函数
f
f
f的
L
−
L-
L−平滑性,因此有
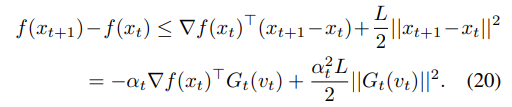
考虑其期望值,可以得到

对t求期望可以得到

将公式(18)应用到上述不等式中可以得到
因此对上述不等式进行调整可以得到
结合函数
f
f
f的
L
−
L-
L−平滑性,我们可以得到
将其于公式(21)结合可以得到
将上述不等式从t=1,2,…,T进行累加,可以得到:
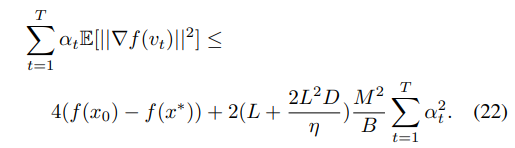
两边同时除以学习率的累加
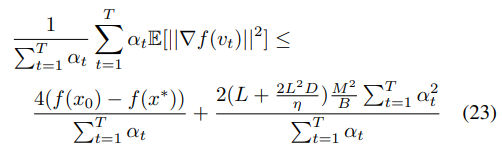
在条件(18)中,如果
γ
(
1
+
η
)
<
1
\gamma(1+\eta)<1
γ(1+η)<1,则无论学习率是固定的还是递减的都可以满足,为了获取
η
\eta
η的界限,我们可以
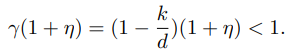
因此我们可以选择
η
<
k
d
−
k
\eta<\frac{k}{d-k}
η<d−kk以满足上述不等式.
Theorem 1暗示着当T足够大时算法1会收敛到0,其中的
α
t
\alpha_t
αt需要满足下述条件
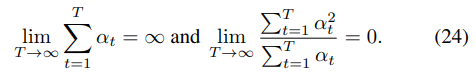

证明:我们首先证明
α
t
=
θ
B
/
T
\alpha_t=\theta \sqrt{B/T}
αt=θB/T为一个常数,能够满足条件(18),为了方便描述,我们令
α
=
α
t
\alpha=\alpha_t
α=αt,因此
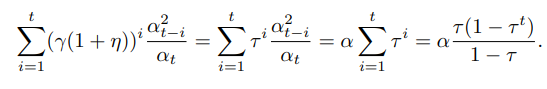
因为
0
<
τ
<
1
0<\tau<1
0<τ<1,所以
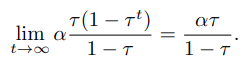
因此当
D
=
α
τ
1
−
τ
D=\frac{\alpha\tau}{1-\tau}
D=1−τατ时条件(18)就会满足.通过应用Theorem 1,我们可以得到:

通过Corollary 2,我们可以发现,通过设置合适的学习率,gTop-
k
k
k的收敛率为
O
(
1
B
T
)
O(\frac{1}{\sqrt{BT}})
O(BT1),与小批量SGD的结果相同,也表明当
T
T
T足够大时,
k
k
k对于收敛的影响不大.






















 1670
1670











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








